Gamma矫正

Gamma矫正指的是：矫正由于计算机的显卡或者显示器的原因出现的源图像和实际输出的图像在亮度上的偏差的过程。通常而言，人眼对于外界亮度的感应并非是线性的，而CRT显示器模拟了这种非线性关系，从而在视觉上有比较好的效果，但是在程序中我们采用的线性RGB的计算关系，所以会导致实际输出的颜色产生偏差，通常会过暗，一般而言我们会采用以下方法进行修正：

RGBgamma=RGB12.2RGB_{gamma}=RGB^{\frac{1}{2.2}}\\

代码如下：

1
2
const float gamma = 2.2f;
Draw(x, y + startRow, Vector4f(powf(finalColor.x, 1.0f / gamma), powf(finalColor.y, 1.0f / gamma), powf(finalColor.z, 1.0f / gamma), powf(finalColor.w, 1.0f / gamma)));

渲染方程

渲染方程（The rendering equation）是James Kajiya在1986年引入计算机图形学中的一个概念，以一个积分方程的形式定义，奠定了全局光照研究的基础。下面我们就从辐射和BSDF入手，从头开始推导一遍渲染方程。

辐射

光以波的形式传播，为了用物理的方式描述光线的属性，我们引入了辐射度量学（Radiometry），以下是辐射度量学中的几个基本概念：

  • 辐射能（Radiant energy）： 光以辐射的形式传递的总能量，也可以将其理解为发射的光子总数，单位是焦耳，通常用 QQ 进行标识。
  • 辐射通量（Radiant flux）： 辐射通量的概念在图形学中使用的比较多，因为图形学通常不关系辐射和时间的关系，只关心强度，辐射通量表示的就是单位时间内产生的辐射能，单位是瓦特，通常用 Φ\Phi 进行标识。
  • 辐照度（Irradiance）： 除了单位时间内的辐射量，我们还需要知道辐射发生在什么位置，辐照度表示的就是单位面积上的辐射通量，这也可以被理解为辐射通量的面积密度，单位是 W/m2W/m^2 ，通常用 EE 进行标识。

兰伯特余弦定理（Lambert’s cosine law） 描述了光线和物体所成的角度与物体接收的辐照度之间的关系，假如一个平面正对着光源，那么它所能接收到的光照肯定是最多的，相反，如果一个平面侧对着光源，那么它所能接收的光源就会相对减少。兰伯特余弦定理的公式如下（ AA 表示光线覆盖的垂直面积）：

E=dΦdA=ΦAcos⁡θ=ΦA(n⃗⋅l⃗)E=\frac{d\Phi}{dA}=\frac{\Phi}{A}\cos\theta=\frac{\Phi}{A}(\vec{n}\cdot\vec{l})\\

辐射强度（Radiant intensity）： 辐射强度用于描述在单位角度上光线的强度，单位是坎德拉，通常用 II 进行标识。

在理解辐射强度之前，必须要理解立体角（Solid angle） 的概念，所谓立体角，就是用于描述空间中角度大小的一个概念模型。

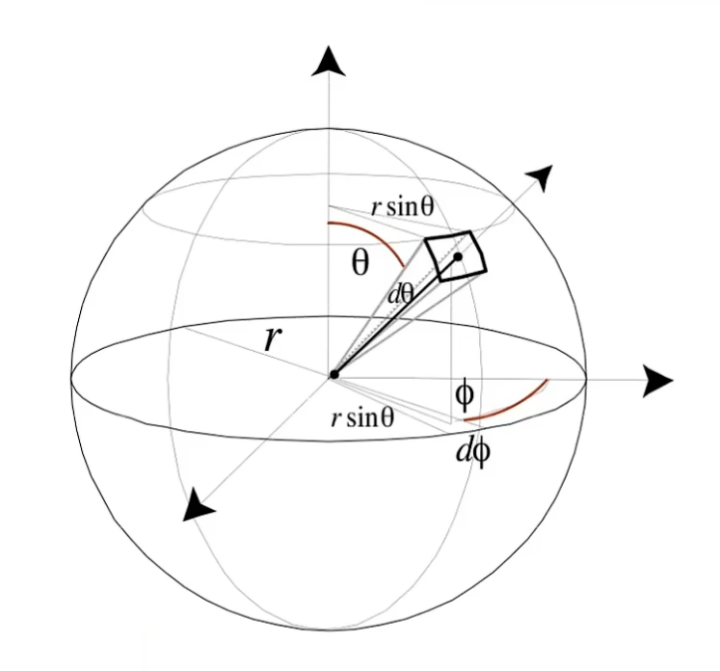
微分立体角说明（图片来自GAMES101）

在上一篇文章中，我们了解了球面映射的方法，这里也使用类似的定义，将球面上一点用 (θ,ϕ)(\theta,\phi) 表示。那么对于球面上面积的微分，可以用这样的方式进行表示：

dA=(r⋅dθ)(rsin⁡θ⋅dϕ)=r2sin⁡θ⋅dθ⋅dϕ\text{d}A=(r\cdot \text{d}\theta)(r\sin\theta\cdot \text{d}\phi)=r^2\sin\theta\cdot \text{d}\theta\cdot \text{d}\phi\\

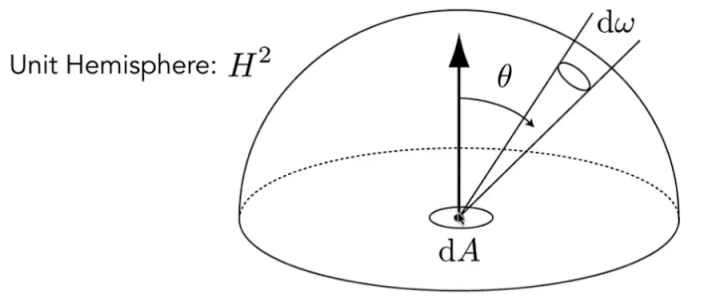
在单位球面上，将半径 rr 略去，就可以得到微分立体角的定义：

dω=dAr2=sin⁡θ⋅dθ⋅dϕ\text{d}\omega=\frac{\text{d}A}{r^2}=\sin\theta\cdot \text{d}\theta\cdot \text{d}\phi\\

所以辐射强度的定义公式就是：

I=dΦdωI=\frac{\text{d}\Phi}{\text{d}\omega}\\

  • 辐射度（Radiance）： 辐射度表示的就是单位立体角上的辐照度，用于描述光线传播中所携带的能量，单位是尼特，通常用 LL 进行标识。

对于一条光线，它的原点为 pp ，方向为 ω\omega ，它的辐射度可以用公式表示为（ AA 表示物体的实际面积， Acos⁡⁡θA\cos⁡\theta 为光线的垂直面积）：

L(p,ω)=dΦ(p,ω)dA⋅cos⁡θdΦ(p,ω)dω=d2Φ(p,ω)dω⋅dA⋅cos⁡θL(p,\omega)=\frac{\text{d}\Phi(p,\omega)}{dA\cdot\cos\theta}\frac{\text{d}\Phi(p,\omega)}{d\omega}=\frac{\text{d}^2\Phi(p,\omega)}{\text{d}\omega\cdot \text{d}A\cdot\cos\theta}

上式又可以被改写成两种形式，入射光线的辐射度可以被这样表示（已知辐照度 E(p)E(p) ）：

L(p,ω)=dE(p)dω⋅cosθL(p,\omega)=\frac{\text{d}E(p)}{\text{d}\omega\cdot cos\theta}

出射光线的辐射度可以被这样表示（已知辐射强度 I(p,ω)I(p,\omega) ）：

L(p,ω)=dI(p,ω)dA⋅cosθL(p,\omega)=\frac{\text{d}I(p,\omega)}{\text{d}A\cdot cos\theta}

半球积分（图片来自GAMES101）

一个物体所接收到的光线是来自四面八方的，我们假设这些光线组成了一个半球，那么我们对辐射度在单位半球上积分，就可以得到辐照度：

dE(p,ω)=Li(p,ω)cos⁡θ⋅dωE(p)=∫H2Li(p,ω)cos⁡θ⋅dωdE(p,\omega)=L_i(p,\omega)\cos\theta\cdot\text{d}\omega\\ E(p)=\int_{H^2}L_i(p,\omega)\cos\theta\cdot\text{d}\omega\\

BSDF

BSDF（Bidirectional Scattering Distribution Function，双向散射分布函数）是BRDF（双向反射分布函数）和BTDF（Bidirectional Transmittance Distribution Function，双向透射分布函数）的合称，用于描述物体所接收的入射光线和散射出的出射光线之间的分布关系，通常用函数 f(ωi→ωr)f(\omega_i\rightarrow\omega_r) 来表示BSDF，之前我们提到的斯涅尔法则（BTDF）和菲涅耳方程（BRDF）都是BSDF的一部分。

BSDF的输入值是辐照度 dEi(ωi)\text{d}E_i(\omega_i) ，输出值是辐射度 dLr(ωr)\text{d}L_r(\omega_r) ，这个过程可以用下式表示：

f(ωi→ωr)=dLr(wr)dEi(ωi)=dLr(wr)Li(ωi)cos⁡θi⋅dωif(\omega_i\rightarrow\omega_r)=\frac{\text{d}L_r(w_r)}{\text{d}E_i(\omega_i)}=\frac{\text{d}L_r(w_r)}{L_i(\omega_i)\cos\theta_i\cdot\text{d}\omega_i}

在实际应用BSDF到渲染方程时，我们通常会把BRDF和BTDF的部分分开，并把渲染方程写成分段函数的形式，理由很简单，反射光线和透射光线分别处于散射平面的两侧，把它们分开就不需要在整个球面上考虑，而是只需要进行简单的半球积分。

以BRDF为例，将BRDF的 dEi(ωi)\text{d}E_i(\omega_i) 代换后进行积分，就可以写出一个反射方程（The reflection equation），到这里就已经距离真正的渲染方程很接近了：

f(ωi→ωr)=dLr(ωr)Li(ωi)cos⁡θidωidLr(ωr)=f(ωi→ωr)Li(ωi)cos⁡θidωiLr(p,ωr)=∫H2fr(p,ωi→ωr)Li(p,ωi)cos⁡θi⋅dωif(\omega_i\rightarrow\omega_r)=\frac{\text{d}L_r(\omega_r)}{L_i(\omega_i)\cos\theta_i\text{d}\omega_i}\\ \text{d}L_r(\omega_r)=f(\omega_i\rightarrow\omega_r)L_i(\omega_i)\cos\theta_i\text{d}\omega_i\\ L_r(p,\omega_r)=\int_{H^2}f_r(p,\omega_i\rightarrow\omega_r)L_i(p,\omega_i)\cos\theta_i\cdot\text{d}\omega_i\\

渲染方程的最后一块拼图：自发光项（Emission term），将其与反射方程相加，得出BRDF段的完整渲染方程如下：

Lo(p,ωo)=Le(p,ωo)+∫H2fr(p,ωi,ωo)Li(p,ωi)cos⁡θi⋅dωiL_o(p,\omega_o)=L_e(p,\omega_o)+\int_{H^2}f_r(p,\omega_i,\omega_o)L_i(p,\omega_i)\cos\theta_i\cdot\text{d}\omega_i

全局光照

全局光照（Global illumination，简称GI）的概念与局部光照相对，局部光照只计算物体的自发光和受到的直接光照，而全局光照则要将所有的间接光照考虑在内。为了计算间接光照，我们需要考虑光线在物体上的弹射衰减，全局光量守恒，对于全体辐射度总和 LL ，用算子形式改写渲染方程得到下式：

L=E+KLL=E+KL

对该式进行变形，求出 LL 的表达式：

IL−KL=E(I−K)L=EL=(I−K)−1EIL-KL=E\\ (I-K)L=E\\ L=(I-K)^{-1}E\\

由广义二项式定理可以展开得：

L=E+KE+K2E+K3E+K4E+...L=E+KE+K^2E+K^3E+K^4E+...\\

由此可见， KK 即为衰减系数， EE 是光源的发光量， KEKE 是直接光照的量，其余项分别表示光线多次弹射得到的间接光量。

向Material类中添加新的Emitted函数，并构建自发光材质：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Material {
public:
	virtual bool Scatter(const Ray& ray, const Hittable::HitInfo& hitInfo, Vector3f& attenuation, Ray& scattered)const { return false; }
	virtual Vector3f Emitted(const Ray& ray, const Hittable::HitInfo& hitInfo)const { return Vector3f(0.0f); }
};

class DiffuseLight : public Material {
public:
	DiffuseLight(const Vector3f& strength) : strength(strength) {}
	bool Scatter(const Ray& ray, const Hittable::HitInfo& hitInfo, Vector3f& attenuation, Ray& scattered)const { return false; }
	Vector3f Emitted(const Ray& ray, const Hittable::HitInfo& hitInfo)const;
	
private:
	Vector3f strength;
};

Vector3f DiffuseLight::Emitted(const Ray& ray, const Hittable::HitInfo& hitInfo)const {
	return strength;
}

修改原来的RayColor代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
Vector4f RayColor(const Ray& ray, Hittable& scene) {
	Hittable::HitInfo hitRecord;
	if (scene.Hit(ray, 0.00001f, FLT_MAX, hitRecord)) {
		Vector3f attenuation;
		Ray scattered;
		Vector3f emitted = hitRecord.material->Emitted(ray, hitRecord);

		if (hitRecord.material->Scatter(ray, hitRecord, attenuation, scattered)) {
			return Vector4f(emitted + attenuation / probabilityRR * RayColor(scattered, scene).GetVector3f(), 1.0f);
		}
		else
			return Vector4f(emitted, 1.0f);

	}

	return Vector4f(0.0f);
}

但是还有一个问题没有解决，那就是递归到底在什么时候终止，在之前我们使用的都是写死的depth值，但这显然并不是合适的做法。对于这个问题有一种将数学问题转化为概率问题的解法，被称作俄罗斯轮盘赌（Russian Roulette） 方法，这是一个很有意思的类比，光线每次弹射都有一定概率衰亡，就好像在俄罗斯轮盘赌中，每次开枪都有一定概率子弹上膛，它的核心思想是将递归何时终止交由概率去决定：

假设光线打到物体上会继续弹射的概率为 PP ，那么衰亡的概率就是 1−P1−P ，要使光量依旧守恒，则必须满足下式：

E=P×LoP+(1−P)×0=LoE=P\times\frac{L_o}{P}+(1-P)\times0=L_o\\

这也就是说即使在弹射过程中光线在不断以一定概率衰减，只要将能存活下来的光线辐射度除以存活概率，得出的结果依旧是物理正确的。接下来就可以开始修改代码了：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
Vector4f RayColor(const Ray& ray, Hittable& scene, float probabilityRR) {
	Hittable::HitInfo hitRecord;
	if (scene.Hit(ray, 0.00001f, FLT_MAX, hitRecord)) {
		Vector3f attenuation;
		Ray scattered;
		Vector3f emitted = hitRecord.material->Emitted(ray, hitRecord);

		float pRR = Random(0.0f, 1.0f);
		if (pRR < probabilityRR && hitRecord.material->Scatter(ray, hitRecord, attenuation, scattered)) {
			return Vector4f(emitted + attenuation / probabilityRR * RayColor(scattered, scene, probabilityRR).GetVector3f(), 1.0f);
		}
		else
			return Vector4f(emitted, 1.0f);

	}

	return Vector4f(0.0f);
}

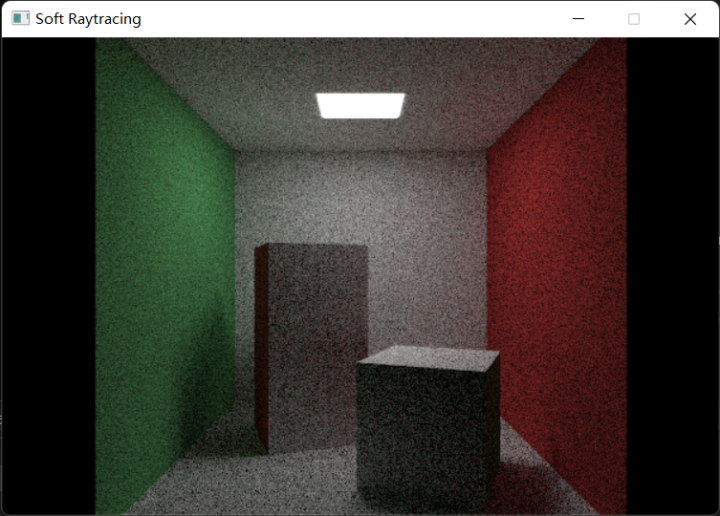
最终结果：

著名的Cornell Box

至此，全局光照已经初成原型，然而仍有巨大的问题需要修正：噪点过多，效率过低。接下来我们引入的蒙特卡洛方法就是为了优化这些问题。

蒙特卡洛方法

蒙特卡洛（Monte Carlo，简称MC） 方法是一种基于统计学原理的求积分方法，使用这种方法可以优化通过离散量逼近连续量的过程。蒙特卡洛方法告诉我们，利用一个随机变量对被积函数进行采样，并将采样值进行一定的处理，当采样值越来越多时，得到的结果就越来越接近原积分的真实结果。

散射PDF

为了引入PDF的概念，我们需要了解一些概率论的背景：在一样本空间（Sample space）内，取一随机事件 xix_i ，它的概率为 pi(pi≥0)p_i(p_i≥0) ，且 pip_i 满足 ∑i=1npi=1\sum_{i=1}^np_i=1 。不断进行取随机变量的操作，最终会无限趋近于一个期望值（Expected value），称为数学期望，可以表示为：

E(X)=∑i=1nxipiE(X)=\sum_{i=1}^{n}{x_ip_i}\\

当 XX 为一连续的随机变量时，我们将随机变量的值作为x轴，概率作为y轴，就可以作出一个函数，这个函数就被称作概率密度函数（The Probability Distribution Function，简称PDF），而取随机变量的操作本质上就变成了在这一函数上取值。对于一概率密度函数 p(x)p(x) ，它的基本性质是 ∫p(x)dx=1\int p(x)\text{d}x=1 ，并且期望可以表示为 E(x)=∫x⋅p(x)dxE(x)=\int x\cdot p(x)\text{d}x 。

函数的期望具有传递性：假设有一函数 y=f(x)y=f(x) ，它的期望可以表示为：

E(y)=E(f(x))=∫f(x)⋅p(x)dxE(y)=E(f(x))=\int f(x)\cdot p(x)\text{d}x

由此我们就可以得知蒙特卡洛积分的基本原理：在要求积分的函数上用PDF进行随机采样，对于单个样本，积分可以用下式求解：

∫f(x)dx≈f(Xi)p(Xi)其中Xi∼p(x)\int f(x)\text{d}x\approx\frac{f(X_i)}{p(X_i)}其中X_i\sim p(x)

但很明显，这样求出来的结果是不准确的，因此需要进行多次采样，并对所有样本求均值，样本数量越多则最终求出的函数值越准确，当采样次数趋近于无穷时，就可以计算出正确的积分：

∫f(x)dx≈1N∑i=1Nf(Xi)p(Xi)其中Xi∼p(x)\int f(x)\text{d}x\approx\frac{1}{N}\sum_{i=1}^{N}\frac{f(X_i)}{p(X_i)}其中X_i\sim p(x)\\

有了以上的概念后，我们可以用蒙特卡洛方法对反射方程进行求解：

Lr(p,ωr)=∫H2fr(p,ωi,ωr)Li(p,ωi)cos⁡θi⋅dωi≈1N∑i=1Nfr(p,ωi,ωr)Li(p,ωi)cos⁡θip(ωi)\begin{aligned}L_r(p,\omega_r)=&\int_{H^2}f_r(p,\omega_i,\omega_r)L_i(p,\omega_i)\cos\theta_i\cdot\text{d}\omega_i\\ \approx&\frac{1}{N}\sum_{i=1}^{N}\frac{f_r(p,\omega_i,\omega_r)L_i(p,\omega_i)\cos\theta_i}{p(\omega_i)}\end{aligned}

向Material类中添加获取PDF方法：

1
2
3
4
5
6
class Material {
public:
	virtual bool Scatter(const Ray& ray, const Hittable::HitInfo& hitInfo, Vector3f& attenuation, Ray& scattered, float& pdf)const { return false; }
	virtual float ScatteringPDF(const Ray& ray, const Hittable::HitInfo& hitInfo, const Ray& scattered)const { return 0.0f; }
	virtual Vector3f Emitted(const Ray& ray, const Hittable::HitInfo& hitInfo)const { return Vector3f(0.0f); }
};

假定我们在单位半球上均匀采样，那么因为 ∫p(x)dx=1\int p(x)\text{d}x=1 ，又因为 p(x)p(x) 的期望就等于半球积分的值 ∫xp(x)dx=∫02π∫0π2sin⁡θdω=2π\int xp(x)\text{d}x=\int_{0}^{2\pi}\int_{0}^{\frac{\pi}{2}}\sin\theta\text{d}\omega=2\pi ，所以有常值函数 p(ωi)=12πp(\omega_i)=\frac{1}{2\pi} 。ScatteringPDF代码如下：

1
2
3
4
float Lambertian::ScatteringPDF(const Ray& ray, const Hittable::HitInfo& hitInfo, const Ray& scattered)const {
	float cosine = max(Dot(scattered.GetDirection3f(), hitInfo.normal), 0.0f);
	return cosine * 0.5f / M_PI;
}

当光线打到物体平面上时，能量会被吸收一部分并朝不同方向散射成多根光线，我们将光线在不同散射方向上的散射率表示为散射PDF，对于表面越光滑的平面，散射PDF的概率密度就会越集中于一个方向，这个方向就是镜面反射的方向。Lambertian理想散射是散射的一个特殊情形，在这个情形下光线在任何方向的散射率均等，所以散射PDF同样是一个常值函数 p(ω)=12πp(\omega)=\frac{1}{2\pi} ，BRDF可以表示为 BRDFlambertian=albedo⋅p(ω)BRDF_{lambertian}=albedo\cdot p(\omega) 。

生成单位半球上随机向量的代码如下，这里用到了上一篇文章讲到的球面映射的方法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
Vector3f RandomUnitHemisphere(Vector3f v) {
	float phi = 2.0f * Random() * M_PI;
	float cosTheta = 1.0f - Random();
	float x = sinf(phi) * sqrtf(1 - cosTheta * cosTheta);
	float y = cosTheta;
	float z = cosf(phi) * sqrtf(1 - cosTheta * cosTheta);

	Vector3f u = RandomNormalized3f();
	Vector3f w;
	do {
		w = Cross(u, v);
	} while (w.Length() < 0.00001f);
	w = w.Normalize();
	u = Cross(v, w);

	return x * u + y * v + z * w;
}

修改Scatter函数代码如下：

1
2
3
4
5
6
7
bool Lambertian::Scatter(const Ray& ray, const Hittable::HitInfo& hitInfo, Vector3f& attenuation, Ray& scattered, float& pdf)const {
	Vector3f direction = RandomUnitHemisphere(hitInfo.normal);
	scattered = Ray(hitInfo.p, direction);
	attenuation = albedo;
	pdf = 0.5f / M_PI;
	return true;
}

将PDF计算相关代码添加到RayColor中：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Vector4f RayColor(const Ray& ray, Hittable& scene, std::vector<std::shared_ptr<Hittable>>& lights, float probabilityRR, bool useEmitted) {
	Hittable::HitInfo hitRecord;
	if (scene.Hit(ray, 0.00001f, FLT_MAX, hitRecord)) {
		Vector3f albedo;
		Ray scattered;
		Vector3f emitted = hitRecord.material->Emitted(ray, hitRecord);
		float pdf;

		float pRR = Random(0.0f, 1.0f);
		if (pRR < probabilityRR && hitRecord.material->Scatter(ray, hitRecord, albedo, scattered, pdf)) {
			return Vector4f(emitted 
				+ albedo / pdf / probabilityRR * hitRecord.material->ScatteringPDF(ray, hitRecord, scattered) 
				* RayColor(scattered, scene, lights, probabilityRR, false).GetVector3f(), 1.0f);
		}
		else
			return Vector4f(emitted, 1.0f);
	}

	return Vector4f(0.0f);
}

由于 p(ωi)p(\omega_i) 是常值函数，所以实际上 1p(ωi)\frac{1}{p(\omega_i)} 和Lambertian散射BRDF中的 12π\frac{1}{2\pi} 项相抵消了，不过这样做并不是无意义的，而是反映了蒙特卡洛方法的思想，毕竟我们追求的是一个适用于更多情况的物理学通解。

至此，我们得到了一个完整的路径追踪（Path Tracing） 算法模型。

直接光源采样

在之前的程序中，我们在半球上进行随机采样，但是这样会有很多光线根本不会和任何物体发生碰撞，换句话说这些采样点可以给我们的信息太少，是不重要的采样。那我们换个思路，既然射向光源方向的光线能给予更多的信息，那么不如直接在朝向光源的方向进行更多的采样，自然采样效率也就能得到提高，这反映了重要性采样（Importance sampling） 的思想。

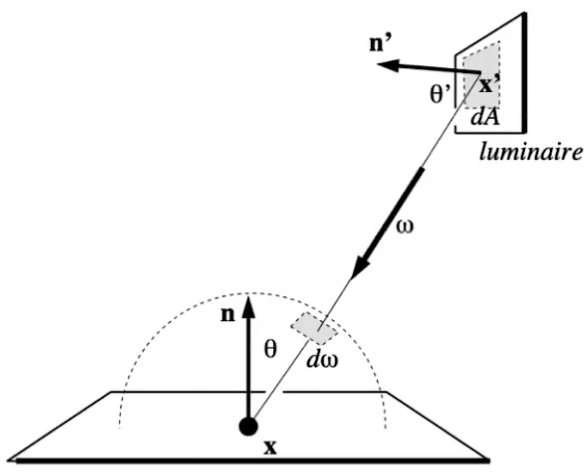
对光源采样（图片来自GAMES101）

假设有一面积为 AA 的光源，为了对光源进行采样，需要将对 dω\text{d}\omega 的积分改写为对 dA\text{d}A 的积分， dω\text{d}\omega 和 dA\text{d}A 有以下几何关系：

dω=dAcos⁡θ′∣∣x′−x∣∣2\text{d}\omega=\frac{\text{d}A\cos\theta'}{||x'-x||^2}

代入进原来的积分方程中完成变量替换：

Lr(x,ωr)=∫Afr(x,ωi,ωr)Li(x,ωi)cos⁡θicos⁡θ′∣∣x′−x∣∣2dAL_r(x,\omega_r)=\int_{A}f_r(x,\omega_i,\omega_r)L_i(x,\omega_i)\frac{\cos\theta_i\cos\theta'}{||x'-x||^2}\text{d}A

p(ωi)light=1Ap(\omega_i)_{light}=\frac{1}{A}

在Hittable类中添加直接对物体所在方向采样的方法，随机在光源上获取一点与反射点连成一条光路，并计算出光源的面积和对应的PDF：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Hittable {
public:
	struct HitInfo {
		float t;
		Vector3f p;
		Vector3f normal;
		bool frontFace;
		std::shared_ptr<Material> material;
		Vector2f texCoord;
	};

	virtual bool Hit(const Ray& ray, float tmin, float tmax, HitInfo& info)const = 0;
	virtual float PDFValue(const Vector3f& origin, Vector3f& direction)const { return 0.0f; }
	BoundingBox boundingBox;
};

float Triangle::PDFValue(const Vector3f& origin, Vector3f& direction)const {
	Vector3f randomBycentric;
	randomBycentric.y = Random();
	randomBycentric.z = Random();
	randomBycentric.x = 1.0f - randomBycentric.y - randomBycentric.z;
	Vector3f randomPoint = p0.position * randomBycentric.x + p1.position * randomBycentric.y + p2.position * randomBycentric.z;
	direction = randomPoint - origin;
	float area = 0.5f * Cross(p1.position - p0.position, p2.position - p0.position).Length();
	return 1.0f / area;
}

将RayColor的计算分成两部分，一部分采用直接光源采样计算直接光照（只有打到光源才计算颜色值），另一部分采用半球采样计算间接光照（只有打到非光源物体才计算颜色值）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
Vector4f RayColor(const Ray& ray, Hittable& scene, std::vector<std::shared_ptr<Hittable>>& lights, float probabilityRR, bool useEmitted) {
	Hittable::HitInfo hitRecord;
	if (scene.Hit(ray, 0.00001f, FLT_MAX, hitRecord)) {
		Vector3f brdf;
		Ray scattered;

		Vector3f rayColor = Vector3f(0.0f);
		if (hitRecord.material->Scatter(ray, hitRecord, brdf, scattered)) {
			for (auto& light : lights) {
				Vector3f toLight;
				float pdfLight = light->PDFValue(hitRecord.p, toLight);
				float xSqured = Dot(toLight, toLight);
				toLight = toLight.Normalize();

				Hittable::HitInfo lightRecord;
				Ray lightRay(hitRecord.p, toLight);
				if (scene.Hit(lightRay, 0.00001f, FLT_MAX, lightRecord)) {
					float cosine = saturate(Dot(toLight, hitRecord.normal)) * saturate(Dot(-toLight, lightRecord.normal));
					rayColor = rayColor + brdf * cosine / xSqured / pdfLight * lightRecord.material->Emitted(lightRay, lightRecord);
				}
			}

			float pRR = Random(0.0f, 1.0f);
			if (pRR < probabilityRR) {
				float cosine = saturate(Dot(scattered.GetDirection3f(), hitRecord.normal));
				float pdfHemi = 0.5f / M_PI;
				rayColor = rayColor + cosine / probabilityRR / pdfHemi * brdf * RayColor(scattered, scene, lights, probabilityRR, false).GetVector3f();
			}
			return Vector4f(rayColor, 1.0f);te
		}
		else {
			if (useEmitted) {
				return Vector4f(hitRecord.marial->Emitted(ray, hitRecord), 1.0f);
			}
		}
	}

	return Vector4f(0.0f);
}

特殊采样材质