本文承接自软光栅化渲染器之后,参考Ray Tracing in One Weekend系列教程,GAMES101和众多大佬的文章梳理出的CPU光线追踪实现流程,仅作学习与记录。
摄像机与射线
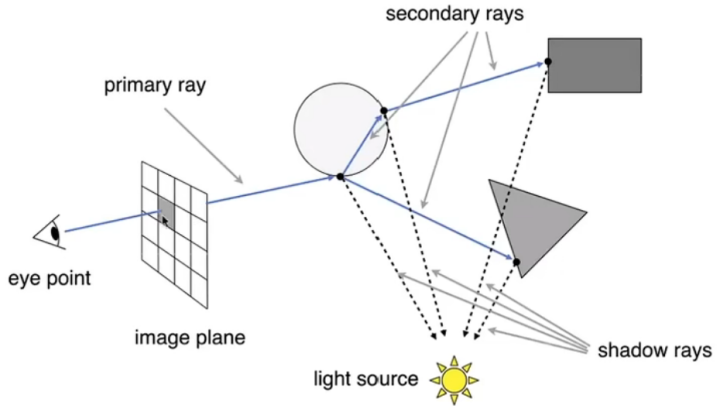
Whitted-Style光线追踪的本质就是从摄像机处发出有限条射线,这些射线在穿过代表屏幕的近平面之后会与各种物体发生相交碰撞,之后射线可能会被反射或被折射,再与更多的物体发生相交碰撞,最后计算出每根射线代表的颜色值,这些颜色值即是应该显示在屏幕上的颜色值。
我们用直线方程 p ( t ) = a + t b ⃗ ( t ≥ 0 ) \boldsymbol{p}(t)=\boldsymbol{a}+t\vec{b}(t\geq0) p ( t ) = a + t b ( t ≥ 0 ) t t t
1 2 3 4 5 6 7 8 9 10 11 12 13 14 class Ray {public : Ray (){} Ray (const Vector3f& origin, const Vector3f& direction) :origin (origin), direction (direction) {} Vector3f GetOrigin3f () const { return origin; } Vector3f GetDirection3f () const { return direction; } Vector3f At (float t) const { return origin + t * direction; } private : Vector3f origin, direction; };
在光线追踪中,摄像机的原点就是初始射线的原点,摄像机的近平面坐标就决定了初始射线的方向,这样的定义比光栅化更加直观,并且不需要额外的透视投影变换。
我们创建一个Camera类来方便对摄像机的控制,同时该类中实现绘制和清屏的操作:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 class Camera {public : Camera (SDL_Window* window, const int & width, const int & height) : width (width), height (height) { renderer = SDL_CreateRenderer (window, 0 , SDL_RENDERER_ACCELERATED); bufferSize = width * height; framebuffer = new Vector4f[bufferSize]; for (int i = 0 ; i < bufferSize; i++) { framebuffer[i] = Vector4f (0.0f , 0.0f , 0.0f , 0.0f ); } aspect = (float )width / (float )height; SetLens (M_PI * 0.25f , 1.0f ); LookAt (Vector3f (0.0f ), Vector3f (0.0f , 0.0f , -1.0f ), Vector3f (0.0f , 1.0f , 0.0f )); } void Destroy () delete [] framebuffer; } void Draw (int x, int y, Vector4f color) framebuffer[y * width + x] = color; } void Clear (const Vector4f& clearValue) for (int i = 0 ; i < width * height; i++) { framebuffer[i] = clearValue; } } void Present () for (int i = 0 ; i < width * height; i++) { Vector4f color = framebuffer[i]; SDL_SetRenderDrawColor (renderer, (Uint8)(color.x * 255 ), (Uint8)(color.y * 255 ), (Uint8)(color.z * 255 ), SDL_ALPHA_OPAQUE); SDL_Point point; point.x = i % width; point.y = i / width; SDL_RenderDrawPoints (renderer, &point, 1 ); } SDL_RenderPresent (renderer); } void SetLens (float FovY, float nearZ) void LookAt (Vector3f position, Vector3f target, Vector3f worldUp) void Render (Hittable& scene, int depth) private : SDL_Renderer* renderer; int width, height, bufferSize; Vector4f* framebuffer; float aspect, nearZ, fovY; Vector3f origin, nearPlane; Vector3f look, up, right; };
用视场角,宽高比和近平面深度构建出摄像机的近平面,用原点坐标,观察目标构建出摄像机发射射线的位置和方向:
1 2 3 4 5 6 7 8 9 10 11 12 13 void Camera::SetLens (float fovY, float nearZ) this ->fovY = fovY; this ->nearZ = nearZ; float nearPlaneHeight = nearZ * tanf (fovY); nearPlane = Vector3f (nearPlaneHeight * aspect, nearPlaneHeight, nearZ); } void Camera::LookAt (Vector3f position, Vector3f target, Vector3f worldUp) look = (target - position).Normalize (); right = Cross (worldUp, -look).Normalize (); up = Cross (-look, right); origin = position; }
在渲染场景中的物体时,对每个像素都发射一条射线,其中horizontal和vertical分别代表在x和y方向上像素的步长:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 void Camera::Render (Hittable& scene, int depth) float horizontal = nearPlane.x / (float )width; float vertical = nearPlane.y / (float )height; Vector3f center = nearPlane.z * look; for (int y = 0 ; y < height; y++) { for (int x = 0 ; x < width; x++) { Vector3f target = center + (-nearPlane.x / 2.0f + ((float )x + 0.5f ) * horizontal) * right + (nearPlane.y / 2.0f - ((float )y + 0.5f ) * vertical) * up; Vector4f color = RayColor (Ray (origin, target.Normalize ()), scene, depth); Draw (x, y, saturate (color)); } } }
RayColor方法返回了射线计算出的颜色,我们会将它作为一个不断递归的方法使用,让射线在空间中不停与物体碰撞,反射,折射,不过目前我们暂时只用它绘制背景颜色:
1 2 3 4 5 6 Vector4f RayColor (const Ray& ray, Hittable& scene, int depth) { Vector3f direction = ray.GetDirection3f ().Normalize (); float t = 0.5f * (direction.y + 1.0f ); Vector3f color = (1.0f - t) * Vector3f (1.0f ) + t * Vector3f (0.5f , 0.7f , 1.0f ); return Vector4f (color, 1.0f ); }
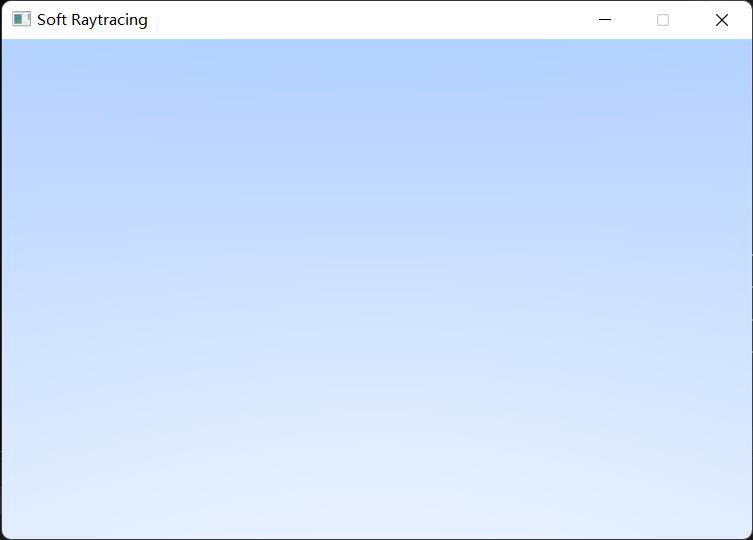
最终得到一个自上而下蓝白渐变的背景:
光追几何体
在光线追踪中,我们会用到大量的几何体求交,所以搞懂背后的数学方法尤为重要。为了方便,我们构建一个Hittable抽象类,并用HitInfo存储几何体求交获得的信息和检测相交的方法,之后我们定义的几何体类都会继承自这个父类:
1 2 3 4 5 6 7 8 9 10 class Hittable {public : struct HitInfo { float t; Vector3f p; Vector3f normal; }; virtual bool Hit (const Ray& ray, float tmin, float tmax, HitInfo& info) const 0 ; };
球体
球体是在光线追踪中最容易计算的几何体,对于一个球心为 c c c R R R p p p
( p − c ) 2 = R 2 (\boldsymbol{p}-\boldsymbol{c})^2=R^2\\
( p − c ) 2 = R 2
代入直线方程,可以得:
( p ( t ) − c ) 2 = R 2 ( a + t b ⃗ − c ) 2 = R 2 ( t b ⃗ + a − c ) 2 = R 2 ( a − c ) 2 + t 2 b ⃗ 2 + 2 ( a − c ) ⋅ ( t b ⃗ ) = R 2 b ⃗ 2 t 2 + 2 b ⃗ ⋅ ( a − c ) t + ( a − c ) 2 − R 2 = 0 \begin{aligned}(\boldsymbol{p}(t)-\boldsymbol{c})^2=&R^2\\ (\boldsymbol{a}+t\vec{b}-\boldsymbol{c})^2=&R^2\\ (t\vec{b}+\boldsymbol{a}-\boldsymbol{c})^2=&R^2\\ (\boldsymbol{a}-\boldsymbol{c})^2+t^2\vec{b}^2+2(\boldsymbol{a}-\boldsymbol{c})\cdot(t\vec{b})=&R^2\\ \vec{b}^2t^2+2\vec{b}\cdot(\boldsymbol{a}-\boldsymbol{c})t+(\boldsymbol{a}-\boldsymbol{c})^2-R^2=&0\\\end{aligned}
( p ( t ) − c ) 2 = ( a + t b − c ) 2 = ( t b + a − c ) 2 = ( a − c ) 2 + t 2 b 2 + 2 ( a − c ) ⋅ ( t b ) = b 2 t 2 + 2 b ⋅ ( a − c ) t + ( a − c ) 2 − R 2 = R 2 R 2 R 2 R 2 0
t t t
Δ = 4 [ b ⃗ ⋅ ( a − c ) ] 2 − 4 b ⃗ 2 [ ( a − c ) 2 − R 2 ] t = − 2 b ⃗ ⋅ ( a − c ) ± Δ 2 b ⃗ 2 t = − b ⃗ ⋅ ( a − c ) ± [ b ⃗ ⋅ ( a − c ) ] 2 − b ⃗ 2 [ ( a − c ) 2 − R 2 ] b ⃗ 2 \begin{aligned}\Delta=&{4[\vec{b}\cdot(\boldsymbol{a}-\boldsymbol{c})]^2-4\vec{b}^2[(\boldsymbol{a}-\boldsymbol{c})^2-R^2]}\\ t=&\frac{-2\vec{b}\cdot(\boldsymbol{a}-\boldsymbol{c})\pm\sqrt{\Delta} }{2\vec{b}^2}\\ t=&\frac{-\vec{b}\cdot(\boldsymbol{a}-\boldsymbol{c})\pm\sqrt{ {[\vec{b}\cdot(\boldsymbol{a}-\boldsymbol{c})]^2-\vec{b}^2[(\boldsymbol{a}-\boldsymbol{c})^2-R^2]} } }{\vec{b}^2}\\\end{aligned}
Δ = t = t = 4 [ b ⋅ ( a − c ) ] 2 − 4 b 2 [( a − c ) 2 − R 2 ] 2 b 2 − 2 b ⋅ ( a − c ) ± Δ b 2 − b ⋅ ( a − c ) ± [ b ⋅ ( a − c ) ] 2 − b 2 [( a − c ) 2 − R 2 ]
由于我们需要找的是射线与球面最近的交点,所以先选择最小的一个 t t t t t t
想要对球体计算法线也很简单,只需要将球心作为首,交点作为尾,计算出一条向量即可:
n ⃗ = n o r m a l i z e ( p − c ) \vec{n}=normalize(\boldsymbol{p}-\boldsymbol{c})\\
n = n or ma l i ze ( p − c )
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 class Sphere : public Hittable {public : Sphere (const Vector3f& center, float radius) : center (center), radius (radius) {} bool Hit (const Ray& ray, float tmin, float tmax, HitInfo& info) const private : Vector3f center; float radius; }; bool Sphere::Hit (const Ray& ray, float tmin, float tmax, HitInfo& info) const Vector3f centerToOrigin = ray.GetOrigin3f () - center; float centerToOrigin2 = Dot (centerToOrigin, centerToOrigin); float a = Dot (ray.GetDirection3f (), ray.GetDirection3f ()); float b = Dot (ray.GetDirection3f (), centerToOrigin); float c = centerToOrigin2 - radius * radius; float delta = b * b - a * c; if (delta > 0.0f ) { float t = (-b - sqrtf (delta)) / a; if (t >= tmin && t <= tmax) { info.t = t; info.p = ray.At (t); info.normal = (ray.At (t) - center) / radius; return true ; } t = (-b + sqrtf (delta)) / a; if (t >= tmin && t <= tmax) { info.t = t; info.p = ray.At (t); info.normal = (ray.At (t) - center) / radius; return true ; } } return false ; }
有的时候我们需要额外判断法线的方向,假如射线是从球体内部射出的,这个时候射线会碰撞到球面的反面,可以通过将射线和法线点积的方法来判断内外,若点积大于0则在内部,若点积小于0则在外部,若点积等于0则射线与球体只有一个交点。
1 2 if (Dot (ray.GetDirection3f (), info.normal) > 0.0f ) info.normal = -info.normal;
三角形
能够画出三角形是绘制各类模型的基础,所以三角形求交算法非常重要,下面讲两个常用的算法:
平面方程法: 三角形求交可以分成两个部分:先检测射线是否和三角形所在平面相交,再检测交点是否在三角形内。
对于一个法线为 n ⃗ \vec{n} n p ′ \boldsymbol{p}′ p ′
( p − p ′ ) ⋅ n ⃗ = 0 (\boldsymbol{p}-\boldsymbol{p'})\cdot\vec{n}=0\\
( p − p ′ ) ⋅ n = 0
代入直线方程,可以得:
( p ( t ) − p ′ ) ⋅ n ⃗ = 0 ( a + t b ⃗ − p ′ ) ⋅ n ⃗ = 0 t = ( p ′ − a ) ⋅ n ⃗ b ⃗ ⋅ n ⃗ \begin{aligned}(\boldsymbol{p}(t)-\boldsymbol{p'})\cdot\vec{n}=&0\\ (\boldsymbol{a}+t\vec{b}-\boldsymbol{p'})\cdot\vec{n}=&0\end{aligned}\\ t=\frac{(\boldsymbol{p'}-\boldsymbol{a})\cdot\vec{n}}{\vec{b}\cdot\vec{n}}\\
( p ( t ) − p ′ ) ⋅ n = ( a + t b − p ′ ) ⋅ n = 0 0 t = b ⋅ n ( p ′ − a ) ⋅ n
得到交点 p \boldsymbol{p} p P 0 , P 1 , P 2 P_0,P_1,P_2 P 0 , P 1 , P 2 P P P P 0 P 1 × P 0 P 2 P_0P_1\times P_0P_2 P 0 P 1 × P 0 P 2 P 0 P 1 × P 0 P P_0P_1\times P_0P P 0 P 1 × P 0 P P P P
Möller-Trumbore算法: 直接使用三角形的重心坐标进行判断,得到以下式子:
a + t b ⃗ = ( 1 − u − v ) P 0 + u P 1 + v P 2 a + t b ⃗ = P 0 + u ( P 1 − P 0 ) + v ( P 2 − P 0 ) a − P 0 = − t b ⃗ + u ( P 1 − P 0 ) + v ( P 2 − P 0 ) \begin{aligned}\boldsymbol{a}+t\vec{b}=&(1-u-v)\boldsymbol{P_0}+u\boldsymbol{P_1}+v\boldsymbol{P_2}\\ \boldsymbol{a}+t\vec{b}=&\boldsymbol{P_0}+u(\boldsymbol{P_1}-\boldsymbol{P_0})+v(\boldsymbol{P_2}-\boldsymbol{P_0})\\ \boldsymbol{a}-\boldsymbol{P_0}=&-t\vec{b}+u(\boldsymbol{P_1}-\boldsymbol{P_0})+v(\boldsymbol{P_2}-\boldsymbol{P_0})\\\end{aligned}
a + t b = a + t b = a − P 0 = ( 1 − u − v ) P 0 + u P 1 + v P 2 P 0 + u ( P 1 − P 0 ) + v ( P 2 − P 0 ) − t b + u ( P 1 − P 0 ) + v ( P 2 − P 0 )
只要求解此式中的 u , v u,v u , v u ≥ 0 , v ≥ 0 , 1 − u − v ≥ 0 u\geq0,v\geq0,1-u-v\geq0 u ≥ 0 , v ≥ 0 , 1 − u − v ≥ 0
[ − b ⃗ P 1 − P 0 P 2 − P 0 ] [ t u v ] = a − P 0 \begin{bmatrix} -\vec{b}&\boldsymbol{P_1}-\boldsymbol{P_0}&\boldsymbol{P_2}-\boldsymbol{P_0} \end{bmatrix} \begin{bmatrix} t\\ u\\ v\\ \end{bmatrix} =\boldsymbol{a}-\boldsymbol{P_0}\\
[ − b P 1 − P 0 P 2 − P 0 ] t u v = a − P 0
运用克莱姆法则解矩阵方程,求出 t , u , v t,u,v t , u , v
[ t u v ] = 1 S 1 ⃗ ⋅ E 1 ⃗ [ S 2 ⃗ ⋅ E 2 ⃗ S 1 ⃗ ⋅ S ⃗ S 2 ⃗ ⋅ b ⃗ ] \begin{bmatrix} t\\u\\v \end{bmatrix} =\frac{1}{\vec{S_1}\cdot\vec{E_1}} \begin{bmatrix} \vec{S_2}\cdot\vec{E_2}\\ \vec{S_1}\cdot\vec{S}\\ \vec{S_2}\cdot\vec{b} \end{bmatrix}\\
t u v = S 1 ⋅ E 1 1 S 2 ⋅ E 2 S 1 ⋅ S S 2 ⋅ b
其中 E 1 ⃗ = P 1 − P 0 , E 2 ⃗ = P 2 − P 0 , S ⃗ = a − P 0 , S 1 ⃗ = b ⃗ × E 2 ⃗ , S 2 ⃗ = S ⃗ × E 1 ⃗ \vec{E_1}=\boldsymbol{P_1}-\boldsymbol{P_0}, \vec{E_2}=\boldsymbol{P_2}-\boldsymbol{P_0}, \vec{S}=\boldsymbol{a}-\boldsymbol{P_0}, \vec{S_1}=\vec{b}\times \vec{E_2}, \vec{S_2}=\vec{S}\times \vec{E_1} E 1 = P 1 − P 0 , E 2 = P 2 − P 0 , S = a − P 0 , S 1 = b × E 2 , S 2 = S × E 1
三角形的法线可以简单地通过两边向量叉积得到,方向的处理方式和球体类似。
代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 class Triangle : public Hittable {public : Triangle (const Vector3f& p0, const Vector3f& p1, const Vector3f& p2) : p0 (p0), p1 (p1), p2 (p2) {} bool Hit (const Ray& ray, float tmin, float tmax, HitInfo& info) const private : Vector3f p0, p1, p2; }; bool Triangle::Hit (const Ray& ray, float tmin, float tmax, HitInfo& info) const Vector3f e1 = p1 - p0; Vector3f e2 = p2 - p0; Vector3f s = ray.GetOrigin3f () - p0; Vector3f s1 = Cross (ray.GetDirection3f (), e2); Vector3f s2 = Cross (s, e1); Vector3f tuv = (1.0f / Dot (s1, e1)) * Vector3f (Dot (s2, e2), Dot (s1, s), Dot (s2, ray.GetDirection3f ())); if (tuv.x >= tmin && tuv.x <= tmax && tuv.y >= 0.0f && tuv.z >= 0.0f && (1.0f - tuv.y - tuv.z) >= 0.0f ) { info.t = tuv.x; info.p = ray.At (info.t); info.normal = Cross (e1, e2).Normalize (); if (Dot (ray.GetDirection3f (), info.normal) > 0.0f ) info.normal = -info.normal; return true ; } return false ; }
多个几何体
多数时候在场景中不止有一个几何体,每一条射线都有可能会和多个几何体相交,但我们通常只需要最近的那个交点,并以该交点为基础去做折射和反射。将所有几何体存储在一个HittableList中,并对每一个几何体都进行相交检测,最终求出最小的 t t t
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 class HittableList : public Hittable {public : HittableList () {} HittableList (const std::vector<std::shared_ptr<Hittable>> objects) { this ->objects.insert (this ->objects.end (), objects.begin (), objects.end ()); } void Clear () clear (); } void Add (std::shared_ptr<Hittable> object) objects.push_back (object); } bool Hit (const Ray& ray, float tmin, float tmax, HitInfo& info) const private : std::vector<std::shared_ptr<Hittable>> objects; }; bool HittableList::Hit (const Ray& ray, float tmin, float tmax, HitInfo& info) const bool isHit = false ; float closet = tmax; for (const auto & object : objects) { if (object->Hit (ray, tmin, closet, info)) { isHit = true ; closet = info.t; } } return isHit; }
修改RayColor的代码,将射线碰撞到的物体的法向量映射到[0,1]范围内作为颜色输出:
1 2 3 4 5 6 7 8 9 10 11 12 13 Vector4f RayColor (const Ray& ray, Hittable& scene, int depth) { Hittable::HitInfo hitRecord; if (scene.Hit (ray, 0.0001f , FLT_MAX, hitRecord)) { Vector3f direction = hitRecord.normal + RandomNormalized3f (); Vector3f color = 0.5f * (hitRecord.normal + Vector3f (1.0f )); return Vector4f (color, 1.0f ); } Vector3f direction = ray.GetDirection3f ().Normalize (); float t = 0.5f * (direction.y + 1.0f ); Vector3f color = (1.0f - t) * Vector3f (1.0f ) + t * Vector3f (0.5f , 0.7f , 1.0f ); return Vector4f (color, 1.0f ); }
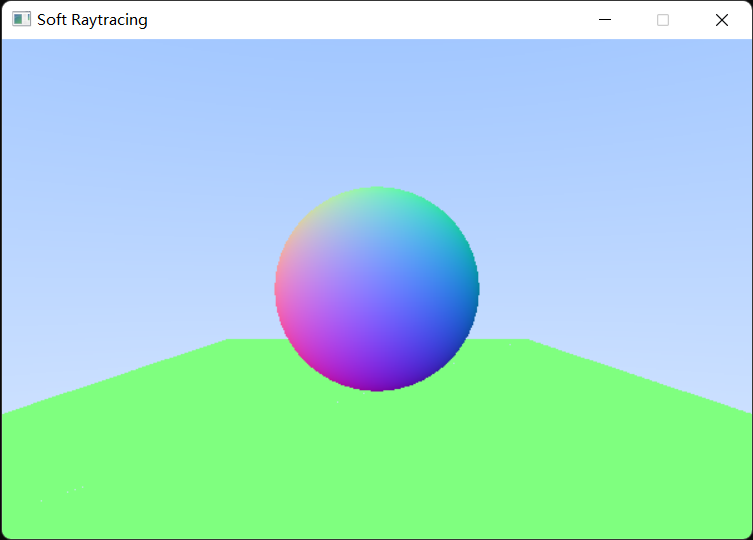
最终可以绘制出一个这样的场景:
反走样
光线追踪反走样的做法和光栅化类似,在光栅化中是对一个像素多重采样,在光线追踪中则是对一个像素发出多条射线,在光栅化中有“标准采样点”,光线追踪中也可以有相似的定义,只不过把采样点换成射线经过近平面的点而已(有关标准采样点的描述详见软渲染器(二))。
以4x反走样为例,代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 void Camera::Render4Sample (Hittable& scene, int depth) float horizontal = nearPlane.x / (float )width; float vertical = nearPlane.y / (float )height; Vector3f center = nearPlane.z * look; for (int y = 0 ; y < height; y++) { for (int x = 0 ; x < width; x++) { float offset[2 ] = { 1.0f / 16.0f * 6.0f , 1.0f / 16.0f * 2.0f }; Vector2f position[4 ]; position[0 ] = Vector2f (x - offset[1 ], y + offset[0 ]); position[1 ] = Vector2f (x + offset[0 ], y + offset[1 ]); position[2 ] = Vector2f (x - offset[0 ], y - offset[1 ]); position[3 ] = Vector2f (x + offset[1 ], y - offset[0 ]); Vector4f color[4 ]; for (int i = 0 ; i < 4 ; i++) { Vector3f target = center + (-nearPlane.x / 2.0f + ((float )position[i].x + 0.5f ) * horizontal) * right + (nearPlane.y / 2.0f - ((float )position[i].y + 0.5f ) * vertical) * up; Vector4f color = RayColor (Ray (origin, target.Normalize ()), scene, depth); } Vector4f finalColor = 0.25f * color[0 ] + 0.25f * color[1 ] + 0.25f * color[2 ] + 0.25f * color[3 ]; Draw (x, y, saturate (finalColor)); } } }
将四条射线求出的颜色进行加权平均,就可得到最终的颜色。
提高反走样的倍数,锯齿和噪点的数量就能得到明显的减少,但是开销也会成倍增加,特别使对于需要大量计算的光线追踪会造成极大的计算负荷,需要做出权衡。
假如渲染出的噪点过多,我们还可以考虑对一个采样点投射多条射线并取平均值:
1 2 3 4 5 6 7 8 9 10 11 12 const int rayCount = 50 ;Vector4f color[4 ]; for (int i = 0 ; i < 4 ; i++) { color[i] = Vector4f (0.0f ); for (int j = 0 ; j < rayCount; j++) { Vector3f target = center + (-nearPlane.x / 2.0f + ((float )position[i].x + 0.5f ) * horizontal) * right + (nearPlane.y / 2.0f - ((float )position[i].y + 0.5f ) * vertical) * up; color[i] = color[i] + (1.0f / rayCount) * RayColor (Ray (origin, target - origin), scene, depth); } }
材质
场景中的每个物体都有其不同的材质,或粗糙或光滑,影响了光线的反射和折射,材质的定义对于之后的光照计算至关重要,我们构建一个Material抽象类,并在HitInfo和物体类中添加对应的成员变量:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 class Material ;class Hittable {public : struct HitInfo { float t; Vector3f p; Vector3f normal; std::shared_ptr<Material> material; }; virtual bool Hit (const Ray& ray, float tmin, float tmax, HitInfo& info) const 0 ; }; class Material {public : virtual bool Scatter (const Ray& ray, const Hittable::HitInfo& hitInfo, Vector3f& attenuation, Ray& scattered) const 0 ; }; class Sphere : public Hittable {public : Sphere (const Vector3f& center, float radius, std::shared_ptr<Material> material) : center (center), radius (radius), material (material) {} bool Hit (const Ray& ray, float tmin, float tmax, HitInfo& info) const private : Vector3f center; float radius; std::shared_ptr<Material> material; }; class Triangle : public Hittable {public : Triangle (const Vector3f& p0, const Vector3f& p1, const Vector3f& p2, std::shared_ptr<Material> material) : p0 (p0), p1 (p1), p2 (p2), material (material) {} bool Hit (const Ray& ray, float tmin, float tmax, HitInfo& info) const private : Vector3f p0, p1, p2; std::shared_ptr<Material> material; };
向Material类中添加了一个基本的Scatter散射函数,该函数返回attenuation和scattered值,分别表示光线的衰减量和散射出的射线。
在Hit函数中让射线和物体碰撞时用HitInfo来自物体的材质信息:
1 info.material = material;
反射
Lambertian理想散射
在前面的程序中,我们的射线在碰到第一个物体后就停下了,实际上这并不符合需求,接下来我们要尝试让射线从碰撞点反射出去,如果它与另一个物体碰撞则继续反射,但是每次反射都会使颜色值发生衰减,也就是说碰撞次数越多,射线接收到的环境光照就会越弱,我们用递归函数来完成这样的操作:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 Vector4f RayColor (const Ray& ray, Hittable& scene, int depth) { if (depth <= 0 ) { return Vector4f (0.0f ); } Hittable::HitInfo hitRecord; if (scene.Hit (ray, 0.0001f , FLT_MAX, hitRecord)) { Vector3f direction = hitRecord.normal + RandomNormalized3f (); return 0.6f * RayColor (Ray (hitRecord.p, direction.Normalize ()), scene, depth - 1 ); } Vector3f direction = ray.GetDirection3f ().Normalize (); float t = 0.5f * (direction.y + 1.0f ); Vector3f color = (1.0f - t) * Vector3f (1.0f ) + t * Vector3f (0.5f , 0.7f , 1.0f ); return Vector4f (color, 1.0f ); }
在物体很多的场景中,如果让光线在场景中永无止境地弹射,那么运算负荷太大,所以可以设置一个depth值,让光线在弹射一定次数后就衰减殆尽。
射线的反射方向在这采用了在法线附近单位球面随机生成的方法,这样就不至于有太多的射线被原路返回,造成错误的结果,单位球面随机向量的生成算法如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 float Random () return (float )rand () / RAND_MAX; } float Random (float min, float max) return min + (max - min) * Random (); } Vector3f Random (Vector3f min, Vector3f max) { return Vector3f (Random (min.x, max.x), Random (min.y, max.y), Random (min.z, max.z)); } Vector3f RandomNormalized3f () { while (true ) { Vector3f v = Random (Vector3f (-1.0f ), Vector3f (1.0f ));; if (v.Length () <= 1.0f ) return v.Normalize (); } }
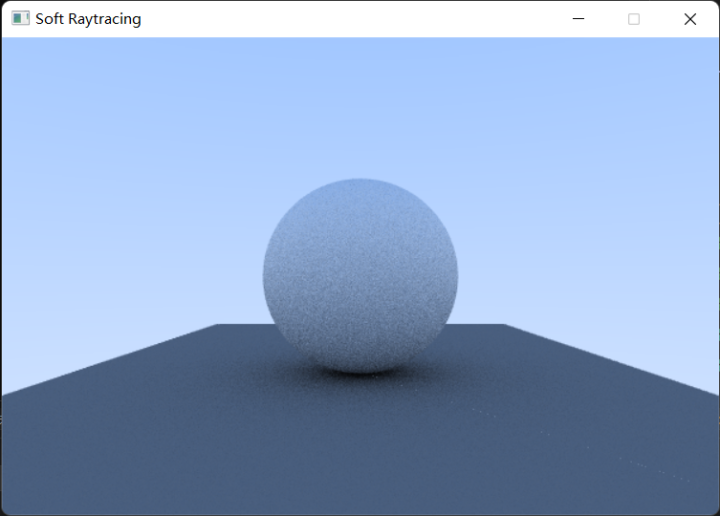
最终可以看到场景中的物体已经有了明显的粗糙材质和阴影:
构建一个Lambertian漫反射材质来取代将散射直接写死在函数中的方法:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 class Lambertian : public Material {public : Lambertian (const Vector3f& albedo) : albedo (albedo) {} bool Scatter (const Ray& ray, const Hittable::HitInfo& hitInfo, Vector3f& attenuation, Ray& scattered) const private : Vector3f albedo; }; bool Lambertian::Scatter (const Ray& ray, const Hittable::HitInfo& hitInfo, Vector3f& attenuation, Ray& scattered) const Vector3f direction = hitInfo.normal + RandomNormalized3f (); scattered = Ray (hitInfo.p, direction); attenuation = albedo; return true ; }
修改原来的RayColor函数代码如下:
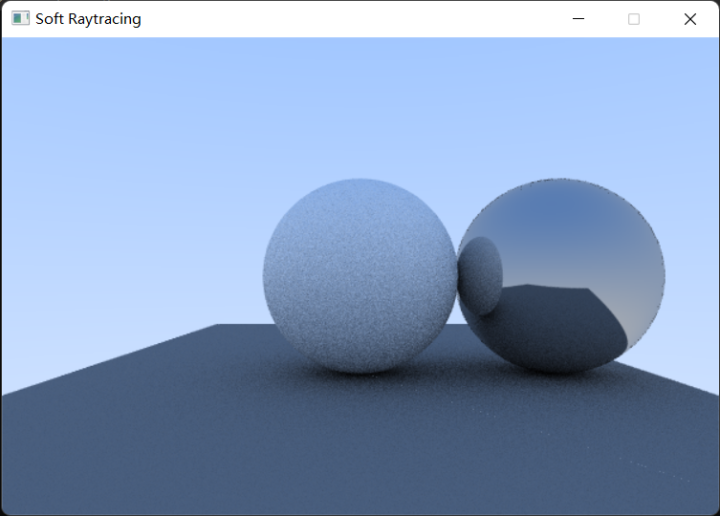
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 Vector4f RayColor (const Ray& ray, Hittable& scene, int depth) { if (depth <= 0 ) { return Vector4f (0.0f ); } Hittable::HitInfo hitRecord; if (scene.Hit (ray, 0.00001f , FLT_MAX, hitRecord)) { Vector3f attenuation; Ray scattered; if (hitRecord.material->Scatter (ray, hitRecord, attenuation, scattered)) { Vector4f rayColor = RayColor (scattered, scene, depth - 1 ); return Vector4f (rayColor.GetVector3f () * attenuation, rayColor.w); } return Vector4f (0.0f ); } Vector3f direction = ray.GetDirection3f ().Normalize (); float t = 0.5f * (direction.y + 1.0f ); Vector3f color = (1.0f - t) * Vector3f (1.0f ) + t * Vector3f (0.5f , 0.7f , 1.0f ); return Vector4f (color, 1.0f ); }
镜面反射
对于光滑的金属材质来说,光线是不会像漫反射那样随机散射的,而是产生镜面反射,反射光线与入射光线相对法线对称,遵循 r ⃗ = v ⃗ + 2 ( − v ⃗ ⋅ n ⃗ ) n ⃗ \vec{r}=\vec{v}+2(-\vec{v}\cdot\vec{n})\vec{n} r = v + 2 ( − v ⋅ n ) n
代码如下:
1 2 3 Vector3f Reflect (Vector3f v, Vector3f n) { return v + 2 * Dot (-v, n) * n; }
新建一个金属材质,用镜面反射的方法替代原来的理想散射:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 class Metal : public Material {public : Metal (const Vector3f& albedo, float fuzziness) : albedo (albedo), fuzziness (fuzziness) {} bool Scatter (const Ray& ray, const Hittable::HitInfo& hitInfo, Vector3f& attenuation, Ray& scattered) const private : Vector3f albedo; float fuzziness; }; bool Metal::Scatter (const Ray& ray, const Hittable::HitInfo& hitInfo, Vector3f& attenuation, Ray& scattered) const Vector3f reflected = Reflect (ray.GetDirection3f (), hitInfo.normal); scattered = Ray (hitInfo.p, reflected + fuzziness * RandomNormalized3f ()); attenuation = albedo; return (Dot (reflected, hitInfo.normal) > 0.0f ); }
这里新增了一个fuzziness参量,用于给反射出的光线增添一些随机性,fuzziness的值越大,反射的随机性越强,材质的镜面反射就会越模糊。
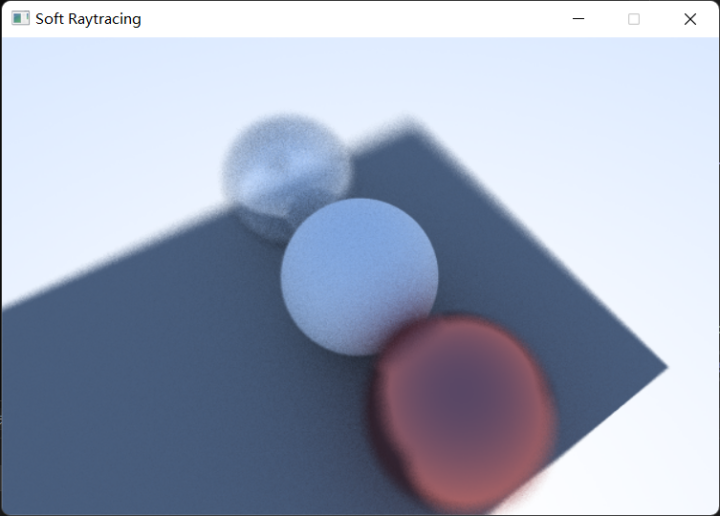
最终可以得到一个反射出周围场景的物体:
折射
对于入射光线,折射光线和介质的关系,我们通常用Snell法则 进行描述(没错,就是高中学的那个):
η i sin θ i = η t sin θ t \eta_i\sin\theta_i=\eta_t\sin\theta_t\\
η i sin θ i = η t sin θ t
简单推导一下求出折射角的余弦值:
cos θ t = 1 − sin 2 θ t = 1 − ( n i n t ) 2 sin 2 θ i = 1 − ( n i n t ) 2 ( 1 − cos 2 θ i ) \begin{aligned} \cos\theta_t=&\sqrt{1-\sin^2\theta_t}\\ =&\sqrt{1-(\frac{n_i}{n_t})^2\sin^2\theta_i}\\ =&\sqrt{1-(\frac{n_i}{n_t})^2(1-\cos^2\theta_i)}\\ \end{aligned}\\
cos θ t = = = 1 − sin 2 θ t 1 − ( n t n i ) 2 sin 2 θ i 1 − ( n t n i ) 2 ( 1 − cos 2 θ i )
当 1 − ( n i n t ) 2 ( 1 − cos 2 θ i ) < 0 {1-(\frac{n_i}{n_t})^2(1-\cos^2\theta_i)}<0 1 − ( n t n i ) 2 ( 1 − cos 2 θ i ) < 0
对于在一平面上的入射光线和法线,只需要找到和它们在同一平面的折射光线即可,这样我们就可以写出计算折射光线的函数,代码如下(注意入射光线和法线都是单位向量):
1 2 3 4 5 6 Vector3f Refract (Vector3f v, Vector3f n, float refIndex, float & cosFraction) { float cosIncident = Dot (-v, n); cosFraction = 1.0f - refIndex * refIndex * (1.0f - cosIncident * cosIncident); Vector3f parallel = (v + cosIncident * n).Normalize (); return sqrtf (1.0f - cosFraction) * parallel + sqrtf (cosFraction) * (-n); }
新建一个玻璃材质,在其中判断当不满足全反射条件时发生折射,满足全反射条件时发生折射:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 class Glass : public Material {public : Glass (float refIndex) : refIndex (refIndex) {} bool Scatter (const Ray& ray, const Hittable::HitInfo& hitInfo, Vector3f& attenuation, Ray& scattered) const private : float refIndex; }; bool Glass::Scatter (const Ray& ray, const Hittable::HitInfo& hitInfo, Vector3f& attenuation, Ray& scattered) const attenuation = Vector3f (1.0f ); float refIndex = this ->refIndex; if (hitInfo.frontFace) { refIndex = 1.0f / this ->refIndex; } Vector3f direction = ray.GetDirection3f ().Normalize (); float cosFraction; Vector3f refracted = Refract (direction, hitInfo.normal, refIndex, cosFraction); if (cosFraction < 0.0f ) { Vector3f reflected = Reflect (ray.GetDirection3f (), hitInfo.normal); scattered = Ray (hitInfo.p, reflected); return true ; } scattered = Ray (hitInfo.p, refracted); return true ; }
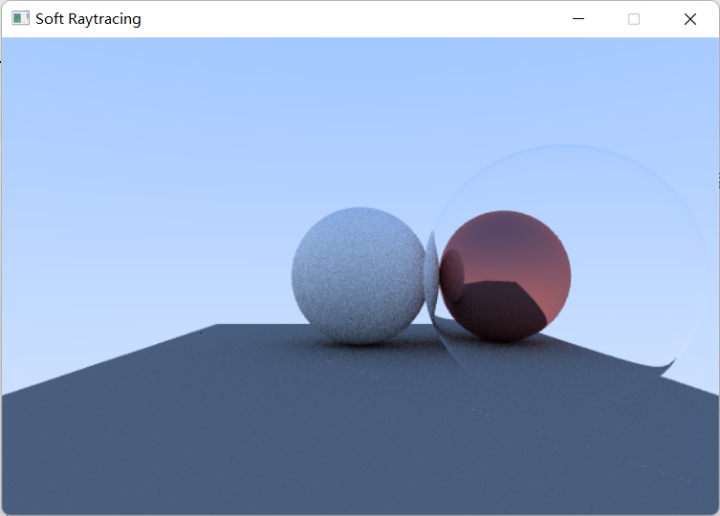
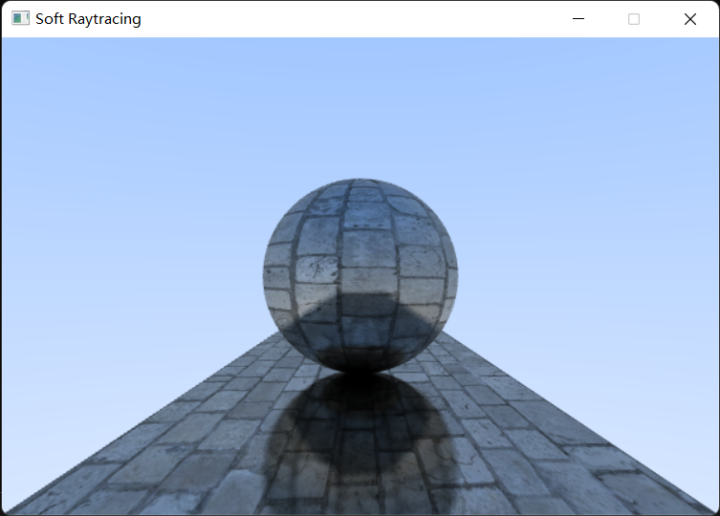
最终可以绘制出一个镜像的透明球体:
然而现实世界中的玻璃,光线发生折射的概率会随着入射角而改变,菲涅耳方程(Fresnel Equations) 用数学方式描述了反射出的光线所占的百分比,但是由于光照过程的计算过于复杂,所以通常不会直接使用菲涅耳方程,而是采用一个效率更高且效果尚可的石里克近似法(Schlick approximation) :
R f ( 0 ∘ ) = ( 1 − η i η t 1 + η i η t ) 2 R f ( θ i ) = R f ( 0 ∘ ) + ( 1 − R f ( 0 ∘ ) ) ( 1 − cos θ i ) 5 R_f(0^\circ)=(\frac{1-\frac{\eta_i}{\eta_t}}{1+\frac{\eta_i}{\eta_t}})^2\\ R_f(\theta_i)=R_f(0^\circ)+(1-R_f(0^\circ))(1-\cos\theta_i)^5\\
R f ( 0 ∘ ) = ( 1 + η t η i 1 − η t η i ) 2 R f ( θ i ) = R f ( 0 ∘ ) + ( 1 − R f ( 0 ∘ )) ( 1 − cos θ i ) 5
修改原来的代码如下:
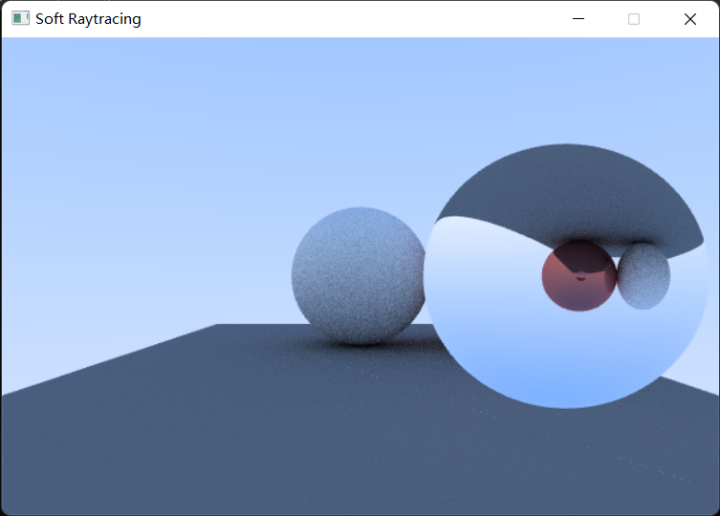
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 float Schlick (float cosine, float refIndex) float R0 = (1.0f - refIndex) / (1.0f + refIndex); R0 *= R0; return R0 + (1.0f - R0) * powf ((1.0f - cosf (cosine)), 5.0f ); } bool Glass::Scatter (const Ray& ray, const Hittable::HitInfo& hitInfo, Vector3f& attenuation, Ray& scattered) const attenuation = Vector3f (1.0f ); float refIndex = this ->refIndex; if (hitInfo.frontFace) { refIndex = 1.0f / this ->refIndex; } Vector3f direction = ray.GetDirection3f ().Normalize (); float cosFraction; Vector3f refracted = Refract (direction, hitInfo.normal, refIndex, cosFraction); if (cosFraction < 0.0f ) { Vector3f reflected = Reflect (ray.GetDirection3f (), hitInfo.normal); scattered = Ray (hitInfo.p, reflected); return true ; } float reflectPercent = Schlick (saturate (Dot (-direction, hitInfo.normal)), refIndex); if (Random () < reflectPercent) { Vector3f reflected = Reflect (ray.GetDirection3f (), hitInfo.normal); scattered = Ray (hitInfo.p, reflected); return true ; } scattered = Ray (hitInfo.p, refracted); return true ; }
Ray Tracing in One Weekend中提到了一个小技巧,在大球里套一个半径相近的小球并把小球的半径设为负值(使法线反转),就可以得到一个透射的球,如下所示:
散焦模糊
在之前的例子中,所有射线都是从一个摄像机原点射出的,但真实的摄像机可不是这样,而是需要一个透镜来聚焦四面八方的光线。在这种情况下,位于焦距处的物体会最为清晰,而距离焦距越远的物体就会越模糊,这种现象被称作散焦模糊(Defocus blur) 或景深(Depth of field) ,为了在光线追踪中模拟这种现象,我们也需要做类似的事情,人为规定一个发射出射线的光圈(透镜)。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 void Camera::SetLens (float fovY, float nearZ, float aperture) this ->fovY = fovY; this ->nearZ = nearZ; this ->aperture = aperture; float nearPlaneHeight = nearZ * tanf (fovY); nearPlane = Vector3f (nearPlaneHeight * aspect, nearPlaneHeight, nearZ); } Vector3f RandomRay () { Vector2f v; while (true ) { v = Vector2f (Random (), Random ()); if (v.Length () > 1.0f )continue ; break ; } v = aperture * v; return origin + v.x * right + v.y * up; }
从一个以aperture作为半径的光圈中随机取一个点,并将该点作为偏移量附加到摄像机原点上,这一步模拟了从光圈中射出射线,aperture的值越大则散焦模糊越强,aperture为0即不发生散焦模糊。
修改原来发出射线的方法,代码如下:
1 2 3 4 5 6 7 8 color[i] = Vector4f (0.0f ); for (int j = 0 ; j < rayCount; j++) { Vector3f target = origin + center + (-nearPlane.x / 2.0f + ((float )position[i].x + 0.5f ) * horizontal) * right + (nearPlane.y / 2.0f - ((float )position[i].y + 0.5f ) * vertical) * up; Vector3f origin = RandomRay (); color[i] = color[i] + (1.0f / rayCount) * RayColor (Ray (origin, (target - origin).Normalize ()), scene, depth); }
在构建摄像机时将摄像机原点和需要聚焦的物体之间的距离(即焦距)设为nearZ值即可使更多的射线会聚到该物体上,渲染出的该物体就会更清晰,就可以实现聚焦:
1 2 3 Camera camera (window, width, height) ;camera.LookAt (origin, target, Vector3f (0.0f , 1.0f , 0.0f )); camera.SetLens (M_PI * 0.25f , (target - origin).Length (), 1.0f );
最终渲染出来可以看到非常明显的景深现象:
加速结构
在之前的程序中,我们仅仅是渲染了几个球体和几个三角形,然而在真正的场景中有成千上万个几何体,如果不进行优化那么渲染速度必定会慢成龟速,常见的优化手段是采用包围盒和树结构,当射线和场景中的物体远离时大幅减少几何体求交的次数。
轴对齐包围盒AABB
轴对齐包围盒(Axis-aligned bounding box,AABB) 是由六个平行对面组成的立方体包围盒,之所以选择AABB是因为它构建简单,求交方便,符合加速算法的思想,下面我们构建一个类来实现AABB的基本操作:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 class BoundingBox {public : BoundingBox () {} BoundingBox (const std::vector<Vector3f>& points) { minX = points[0 ].x; minY = points[0 ].y; minZ = points[0 ].z; maxX = points[0 ].x; maxY = points[0 ].y; maxZ = points[0 ].z; for (int i = 1 ; i < points.size (); i++) { minX = min (minX, points[i].x); minY = min (minY, points[i].y); minZ = min (minZ, points[i].z); maxX = max (maxX, points[i].x); maxY = max (maxY, points[i].y); maxZ = max (maxZ, points[i].z); } } bool Hit (const Ray& ray) float minX, minY, maxX, maxY, minZ, maxZ; };
将两个包围盒结合成一个包围盒的方法:
1 2 3 4 5 6 7 8 9 10 BoundingBox SurroundingBox (const BoundingBox& b0, const BoundingBox& b1) { BoundingBox b; b.minX = min (b0.minX, b1.minX); b.minY = min (b0.minY, b1.minY); b.minZ = min (b0.minZ, b1.minZ); b.maxX = min (b0.maxX, b1.maxX); b.maxY = min (b0.maxY, b1.maxY); b.maxZ = min (b0.maxZ, b1.maxZ); return b; }
Slabs求交法: 为了将射线和AABB求交,我们首先需要将6个面各求交一次,由于其轴对齐的特点,所以面求交的做法十分简单,以垂直于x轴的一个面为例,它的求交是这样的:
t = p ′ x − a x b ⃗ x t=\frac{\boldsymbol{p'}_x-\boldsymbol{a}_x}{\vec{b}_x}\\
t = b x p ′ x − a x
当射线进入AABB时,它必然满足与三个近的面都相交,即与近的那个面相交的 t t t t m i n t_{min} t min t t t t m a x t_{max} t ma x
当射线进入包围盒时,它必然满足与三个近的面都相交,即 t e n t e r = max { t m i n } t_{enter}=\max\{ {t_{min} }\} t e n t er = max { t min } t e x i t = min { t m a x } t_{exit}=\min\{ {t_{max} }\} t e x i t = min { t ma x }
特殊情况:
当射线方向向量的某一个分量是负数时,需要反转该轴。
当射线方向向量的某一个分量是0时,将 t m i n t_{min} t min t m a x t_{max} t ma x
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 bool BoundingBox::Hit (const Ray& ray) const float tminx = (minX - ray.GetOrigin3f ().x) / ray.GetDirection3f ().x; float tmaxx = (maxX - ray.GetOrigin3f ().x) / ray.GetDirection3f ().x; if (ray.GetDirection3f ().x < 0.0f ) { swap (tminx, tmaxx); } else if (ray.GetDirection3f ().x == 0.0f ) { tminx = -FLT_MAX; tmaxx = FLT_MAX; } float tminy = (minY - ray.GetOrigin3f ().y) / ray.GetDirection3f ().y; float tmaxy = (maxY - ray.GetOrigin3f ().y) / ray.GetDirection3f ().y; if (ray.GetDirection3f ().y < 0.0f ) { swap (tminy, tmaxy); } else if (ray.GetDirection3f ().y == 0.0f ) { tminy = -FLT_MAX; tmaxy = FLT_MAX; } float tminz = (minZ - ray.GetOrigin3f ().z) / ray.GetDirection3f ().z; float tmaxz = (maxZ - ray.GetOrigin3f ().z) / ray.GetDirection3f ().z; if (ray.GetDirection3f ().z < 0.0f ) { swap (tminz, tmaxz); } else if (ray.GetDirection3f ().z == 0.0f ) { tminz = -FLT_MAX; tmaxz = FLT_MAX; } float tenter = max (max (tminx, tminy), tminz); float texit = min (min (tmaxx, tmaxy), tmaxz); if (tenter < texit && texit >= 0 ) return true ; return false ; }
t e n t e r t_{enter} t e n t er t e x i t t_{exit} t e x i t
t e x i t < 0 t_{exit}<0 t e x i t < 0 t e x i t ≥ 0 t_{exit}\geq0 t e x i t ≥ 0 t e n t e r < 0 t_{enter}<0 t e n t er < 0 t e n t e r ≤ t e x i t t_{enter}\leq t_{exit} t e n t er ≤ t e x i t
综上所述,当且仅当 t e n t e r ≤ t e x i t t_{enter}\leq t_{exit} t e n t er ≤ t e x i t t e x i t ≥ 0 t_{exit}\geq0 t e x i t ≥ 0
在Hittable抽象类中添加一个公共成员变量boundingBox后,为球体构建包围盒:
1 2 3 4 5 6 7 8 9 Sphere (const Vector3f& center, float radius, std::shared_ptr<Material> material) : center (center), radius (radius), material (material) { float offset = abs (radius); boundingBox.minX = center.x - offset; boundingBox.maxX = center.x + offset; boundingBox.minY = center.y - offset; boundingBox.maxY = center.y + offset; boundingBox.minZ = center.z - offset; boundingBox.maxZ = center.z + offset; }
为三角形构建包围盒:
1 2 3 4 Triangle (const Vector3f& p0, const Vector3f& p1, const Vector3f& p2, std::shared_ptr<Material> material) : p0 (p0), p1 (p1), p2 (p2), material (material) { std::vector<Vector3f> vertices = { p0, p1, p2 }; boundingBox = BoundingBox (vertices); }
为HittableList构建包围盒:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 HittableList (const std::vector<std::shared_ptr<Hittable>>& objects) { this ->objects.insert (this ->objects.end (), objects.begin (), objects.end ()); boundingBox = objects[0 ]->boundingBox; for (int i = 1 ; i < objects.size (); i++) boundingBox = SurroundingBox (boundingBox, objects[i]->boundingBox); } void Add (std::shared_ptr<Hittable> object) if (objects.size () == 0 ) boundingBox = object->boundingBox; else boundingBox = SurroundingBox (boundingBox, object->boundingBox); objects.push_back (object); }
BVH树
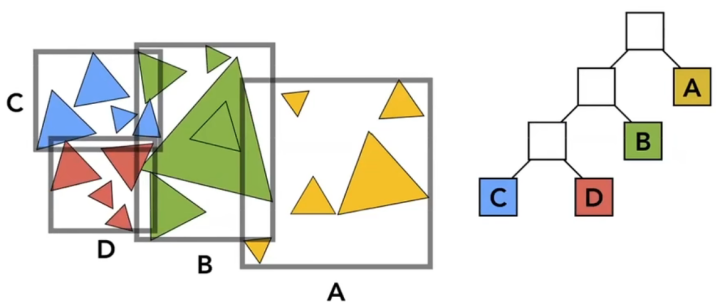
BVH(Bounding volume hierarchy)树 是一种用于场景几何体管理的常用数据结构,用于快速查找相交的几何体,它的基本形态和原理如下图所示:
生成BVH树: 自顶向下,依次挑选x,y,z中最长的那个轴,然后以该轴为基准将空间中的物体排序后,再分成两部分,各自构建一个AABB,再对子节点进行细分,以此类推,直到节点下挂载的物体足够少就停止细分。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 class BVHNode : public Hittable {public : BVHNode (std::vector<std::shared_ptr<Hittable>>& objects) { if (objects.size () == 1 ) { childLeft = objects[0 ]; childRight = objects[0 ]; boundingBox = objects[0 ]->boundingBox; } else if (objects.size () == 2 ) { childLeft = objects[0 ]; childRight = objects[1 ]; boundingBox = SurroundingBox (objects[0 ]->boundingBox, objects[1 ]->boundingBox); } else { boundingBox = objects[0 ]->boundingBox; for (int i = 1 ; i < objects.size (); i++) boundingBox = SurroundingBox (boundingBox, objects[i]->boundingBox); float deltaX = boundingBox.maxX - boundingBox.minX; float deltaY = boundingBox.maxY - boundingBox.minY; float deltaZ = boundingBox.maxZ - boundingBox.minZ; int axis = deltaX > deltaY ? (deltaX > deltaZ ? 0 : 2 ) : (deltaY > deltaZ ? 1 : 2 ); if (axis == 0 ) { std::sort (objects.begin (), objects.end (), [](std::shared_ptr<Hittable>& a, std::shared_ptr<Hittable>& b) { float center0 = (a->boundingBox.minX + a->boundingBox.maxX) / 2.0f ; float center1 = (b->boundingBox.minX + b->boundingBox.maxX) / 2.0f ; return center0 < center1; }); } else if (axis == 1 ) { std::sort (objects.begin (), objects.end (), [](std::shared_ptr<Hittable>& a, std::shared_ptr<Hittable>& b) { float center0 = (a->boundingBox.minY + a->boundingBox.maxY) / 2.0f ; float center1 = (b->boundingBox.minY + b->boundingBox.maxY) / 2.0f ; return center0 < center1; }); } else { std::sort (objects.begin (), objects.end (), [](std::shared_ptr<Hittable>& a, std::shared_ptr<Hittable>& b) { float center0 = (a->boundingBox.minZ + a->boundingBox.maxZ) / 2.0f ; float center1 = (b->boundingBox.minZ + b->boundingBox.maxZ) / 2.0f ; return center0 < center1; }); } size_t half = objects.size () / 2 ; std::vector<std::shared_ptr<Hittable>> childObjLeft, childObjRight; for (int i = 0 ; i < half; i++) childObjLeft.push_back (objects[i]); for (int i = half; i < objects.size (); i++) childObjRight.push_back (objects[i]); childLeft = std::make_shared <BVHNode>(childObjLeft); childRight = std::make_shared <BVHNode>(childObjRight); } } bool Hit (const Ray& ray, float tmin, float tmax, HitInfo& info) const private : std::shared_ptr<Hittable> childLeft; std::shared_ptr<Hittable> childRight; };
在我使用的这个算法中用到了std::sort进行排序,排序依据是各物体包围盒的中心点坐标。节点的细分是递归执行的,直到最后在节点中只挂载了一两个物体就停止细分,在实际上应用时不一定要细分到这么小,例如仅剩五个时就停止也是可以的。
遍历BVH树: 当射线与BVH根节点的包围盒发生碰撞时,进入BVH树的递归遍历,代码如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 bool BVHNode::Hit (const Ray& ray, float tmin, float tmax, HitInfo& info) const if (!boundingBox.Hit (ray)) return false ; HitInfo leftInfo, rightInfo; bool hitLeft = childLeft->Hit (ray, tmin, tmax, leftInfo); bool hitRight = childRight->Hit (ray, tmin, tmax, rightInfo); if (hitLeft && hitRight) { if (leftInfo.t < rightInfo.t) info = leftInfo; else info = rightInfo; return true ; } if (hitLeft) { info = leftInfo; return true ; } if (hitRight) { info = rightInfo; return true ; } return false ; }
需要注意的是,当射线和两个子节点的包围盒都发生相交时,需要将它们的 t t t
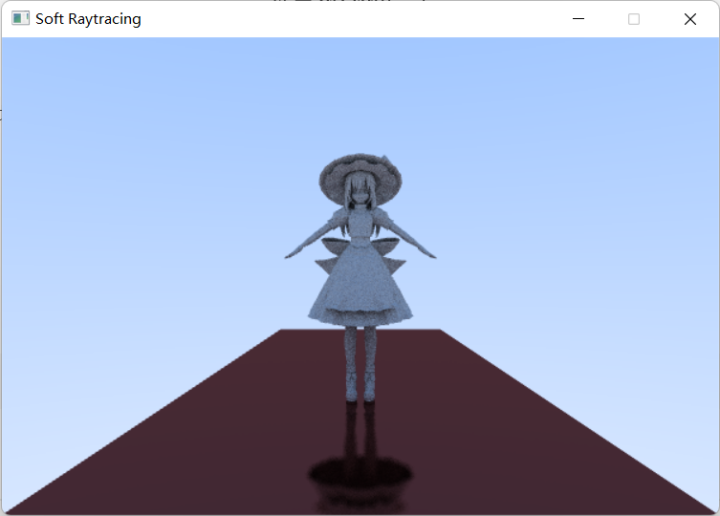
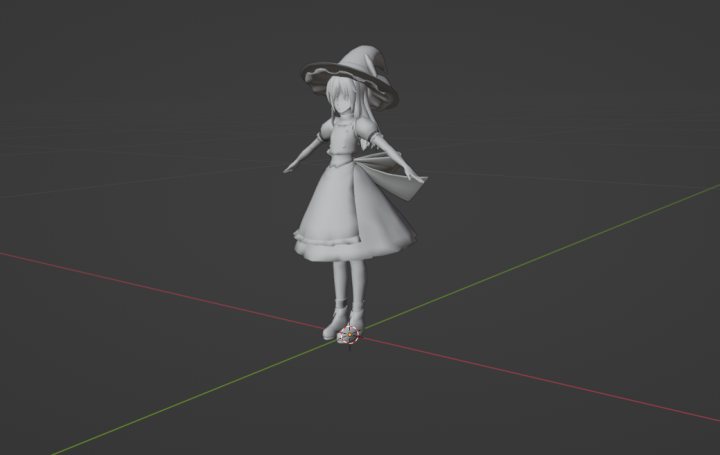
完成了加速结构的构建后,就可以渲染稍微复杂一点的场景了,比如渲染人物模型:
纹理映射
常规纹理映射的实现手段我已经在软光栅化渲染器中讲解过了,对于一个三角形而言,我们只要得到一个点的重心坐标,就能通过插值得到纹理坐标,这里展示代码实现。
在HitInfo中加上纹理坐标成员变量texCoord:
1 2 3 4 5 6 7 8 struct HitInfo { float t; Vector3f p; Vector3f normal; bool frontFace; std::shared_ptr<Material> material; Vector2f texCoord; };
改写Triangle类,添加顶点纹理坐标属性,并在三角形求交时进行纹理坐标插值:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 class Triangle : public Hittable {public : struct Vertex { Vector3f position; Vector2f texCoord; }; Triangle () {} Triangle (const Vertex& p0, const Vertex& p1, const Vertex& p2, std::shared_ptr<Material> material) : p0 (p0), p1 (p1), p2 (p2), material (material) { std::vector<Vector3f> vertices = { p0.position , p1.position, p2.position }; boundingBox = BoundingBox (vertices); } bool Hit (const Ray& ray, float tmin, float tmax, HitInfo& info) const private : Vertex p0, p1, p2; std::shared_ptr<Material> material; }; bool Triangle::Hit (const Ray& ray, float tmin, float tmax, HitInfo& info) const Vector3f e1 = p1.position - p0.position; Vector3f e2 = p2.position - p0.position; Vector3f s = ray.GetOrigin3f () - p0.position; Vector3f s1 = Cross (ray.GetDirection3f (), e2); Vector3f s2 = Cross (s, e1); Vector3f tuv = (1.0f / Dot (s1, e1)) * Vector3f (Dot (s2, e2), Dot (s1, s), Dot (s2, ray.GetDirection3f ())); if (tuv.x >= tmin && tuv.x <= tmax && tuv.y >= 0.0f && tuv.z >= 0.0f && (1.0f - tuv.y - tuv.z) >= 0.0f ) { info.t = tuv.x; info.p = ray.At (info.t); info.material = material; info.normal = Cross (e1, e2).Normalize (); info.frontFace = true ; info.texCoord = (1.0f - tuv.y - tuv.z) * p0.texCoord + tuv.y * p1.texCoord + tuv.z * p2.texCoord; if (Dot (ray.GetDirection3f (), info.normal) > 0.0f ) info.normal = -info.normal; return true ; } return false ; }
新建一个用于纹理采样的材质,以选择Lambertian材质进行扩展为例,将albedo反照率用采样出的纹素颜色值代替:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 class Lambertian_Tex : public Material {public : Lambertian_Tex (const Vector3f& albedo, std::shared_ptr<Texture> texture) : albedo (albedo), texture (texture) {} bool Scatter (const Ray& ray, const Hittable::HitInfo& hitInfo, Vector3f& attenuation, Ray& scattered) const private : std::shared_ptr<Texture> texture; }; bool Lambertian_Tex::Scatter (const Ray& ray, const Hittable::HitInfo& hitInfo, Vector3f& attenuation, Ray& scattered) const Vector3f direction = hitInfo.normal + RandomNormalized3f (); scattered = Ray (hitInfo.p, direction); attenuation = texture->SampleBilinear (hitInfo.texCoord.x, hitInfo.texCoord.y).GetVector3f (); return true ; }
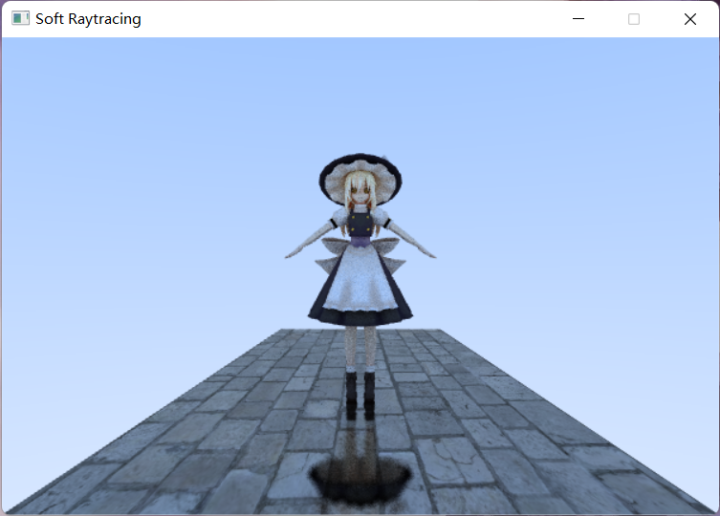
之后就可以为物体贴上贴图:
球面映射
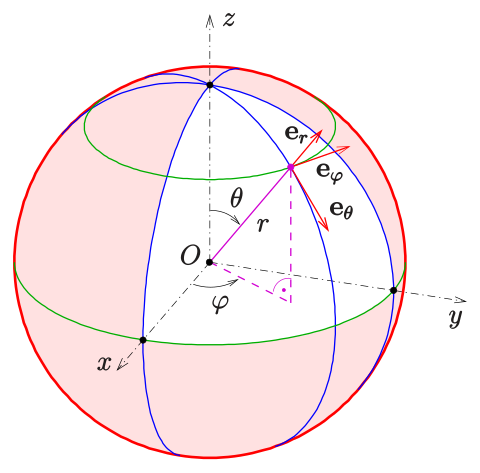
假如用 θ \theta θ ϕ \phi ϕ ( θ , ϕ ) (\theta,\phi) ( θ , ϕ )
在将单张纹理映射到半球面的情况下,球面上一点对应的纹理坐标 ( u , v ) (u,v) ( u , v )
u = ϕ 2 π v = θ π u=\frac{\phi}{2\pi}\\ v=\frac{\theta}{\pi}\\
u = 2 π ϕ v = π θ
但是在射线击中球体时我们获取的坐标是位于直角坐标系下的坐标,所以还需要转换到球面坐标系中。球面坐标转换到直角坐标的关系如下:
x = cos ϕ sin θ y = sin ϕ sin θ z = c o s θ x=\cos\phi\sin\theta\\ y=\sin\phi\sin\theta\\ z=cos\theta\\
x = cos ϕ sin θ y = sin ϕ sin θ z = cos θ
由上式变形可以得:
ϕ = arctan ( y x ) θ = arccos z \phi=\arctan(\frac{y}{x})\\ \theta=\arccos z\\
ϕ = arctan ( x y ) θ = arccos z
atan2函数的值域是 [ − π , π ] [−\pi,\pi] [ − π , π ] [ − π 2 , π 2 ] [-\frac{\pi}{2},\frac{\pi}{2}] [ − 2 π , 2 π ] [ 0 , 1 ] [0,1] [ 0 , 1 ]
u = 1 − ϕ + π 2 π v = θ + π 2 π u=1-\frac{\phi+\pi}{2\pi}\\ v=\frac{\theta+\frac{\pi}{2}}{\pi}\\
u = 1 − 2 π ϕ + π v = π θ + 2 π
在射线与球体求交时添加如下代码(注意坐标轴的不同):
1 2 3 4 5 Vector3f sphereCoord = (info.p - center).Normalize (); float phi = atan2f (sphereCoord.x, sphereCoord.z);float theta = asinf (sphereCoord.y);info.texCoord.x = 1.0f - (phi + M_PI) / (2.0f * M_PI); info.texCoord.y = (theta + M_PI / 2.0f ) / M_PI;
之后就可以为球体贴上贴图: