现代实时渲染技术笔记（一）：阴影

最近一直在写大量的工程代码，解决工程上的问题，颇有些令人疲惫，所以在此之际想开一个新的专栏，以理论为主，每篇文章讨论一个实时渲染的技术话题，以激励自己继续理论知识的学习。同样的，这些文章也是在前人研究的基础上归纳总结出的，参考资料有GAMES101/202，RTR以及各路大佬的技术文章，希望能帮助到更多想要学习的人。

投射平面阴影

阴影映射基础

在光栅化中，之所以阴影的绘制是一个比较麻烦的事，是因为在只考虑局部光照的情况下，我们无法知道完整的环境信息，自然也无法知道哪些地方光线会被遮挡，哪些地方处于光照之下，为了在一定程度上补全环境信息，我们通常会采用阴影映射（Shadow mapping）。阴影映射的概念最初由 Lance Williams 于1978年在论文中提出，通过额外的开销预渲染一张阴影贴图，来做到在真正渲染时判断哪些地方处于阴影当中。

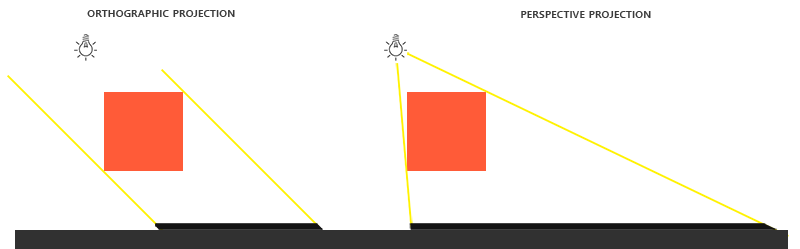
传统的做法需要过两遍Pass，在第一遍Pass中从光源的角度进行场景的渲染，并且将深度测试得到的结果存储在一张深度贴图中，在第二遍Pass中使用。一般在投射方向光阴影时使用正交投影，投射点光源/聚光灯阴影时使用透视投影。

如何使用阴影贴图？首先我们要对阴影贴图进行采样，要采样就需要纹理坐标，这个纹理坐标是要通过世界坐标推得的。我们考虑阴影贴图存储的信息实际上位于NDC空间中，所以将坐标变换过程拆分为以下步骤：

1. 世界空间->光源的观察空间->光源的齐次裁剪空间
2. 光源的齐次裁剪空间->光源的NDC空间
3. 光源的NDC空间->采样用的纹理坐标

由于透视除法并不影响矩阵乘法，所以步骤3实际上可以放到步骤2之前执行。真正实施起来也不复杂，我们获得光源的观察矩阵和投影矩阵并进行结合，再与一个纹理变换矩阵进行结合，就可以得到我们想要的阴影变换矩阵。

需要注意的就是纹理变换矩阵，它的作用是将NDC空间的 [-1,1] * [-1,1] 映射到纹理空间的 [0,1] * [0,1] ，同时将坐标原点移至左下角（Vulkan的原点在左上角），推导并不难，我写出的矩阵是这样的（列主序）：

$$\bm T=\begin{bmatrix} \dfrac{1}{2}&0&0&\dfrac{1}{2}\\ 0&\dfrac{1}{2}&0&\dfrac{1}{2}\\ 0&0&1&0\\ 0&0&0&1\end{bmatrix}$$

伪代码如下：

shadowMatrix = texMatrix * projMatrix * viewMatrix;
shadowPosition = shadowMatrix * worldPosition;
shadowPosition.xyz /= shadowPosition.w;

当然也可以不使用纹理变换矩阵，直接使用线性运算：

shadowPosition.xy = shadowPosition.xy * 0.5 + 0.5;

最终用shadowPosition对阴影贴图进行采样，得到存储的深度值，再与当前的深度值进行比较，判断当前片元是否处于阴影中，参考以下HLSL代码：

//HLSL
float closestDepth = shadowMap.Sample(sampler, shadowPosition.xy);
float currentDepth = shadowPosition.z;
float shadowFactor = currentDepth < closestDepth ? 1.0 : 0.0;

在现代图形API中，通常有对采样结果进行比较的硬件支持，称作比较采样器，例如在HLSL中就可以这样写：

//HLSL
float shadowFactor = shadowMap.SampleCmp(samplerComparison, shadowPosition.xy, currentDepth);

以上，我们了解了阴影映射的基本流程，很显然，这样的做法是有很大的问题的，最典型的就是阴影粉刺和精度问题，我们接下来就会了解一些专门为了处理这些问题而衍生出的方法。

深度偏移 Depth Bias

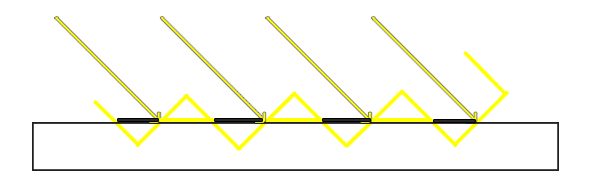
阴影粉刺（Shadow ance） 现象会导致渲染时在不该出现阴影的地方出现错误的黑色线条（摩尔纹），并且光照方向与平面形成的角度越小，这个现象就越严重：

阴影粉刺的成因来自阴影贴图的采样问题，在距离光源比较远的情况下，受限于阴影贴图的分辨率，多个片元可能会采样到阴影贴图中的同一个值，这在光源垂直照向平面时并不会产生问题，但在成一定角度的情况下，会导致一部分片元被认为在阴影中，另一部分被认为在阴影外，就形成了错误的条纹状阴影。

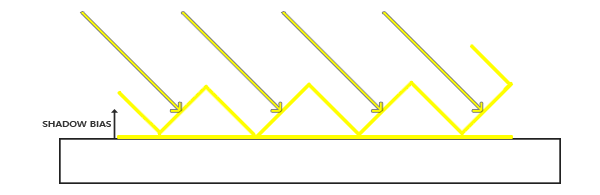
深度偏移（Shadow bias） 是解决这个问题的一个常用方案，它的做法非常简单，在第一遍Pass（渲染阴影贴图）时对深度值应用一个非常小的偏移量，一般在0.001~0.01之间，效果如下：

在现代图形API的渲染管线中一般会内置 Depth bias 参数，只需对其修改即可，即使不使用这个参数，我们也可以在着色器中达到一样的效果：

float bias = 0.005;
float shadow = currentDepth  < closestDepth + bias ? 1.0 : 0.0;

LearnOpenGL提供了一个改进方案，利用法线和光线的夹角动态改变bias大小，在角度较小时应用更大的bias值：

float bias = max(0.05 * (1.0 - dot(normal, lightDirection)), 0.005);

当然要选择合适的偏移值，不能过小也不能过大，过大就会导致阴影无法紧贴物体，出现悬浮阴影的问题，俗称 Peter Panning（叫这个名字是因为阴影悬浮的现象就像小飞侠一样）。

解决阴影粉刺的另一个方案是利用正面剔除，因为物体的背面深度值比正面来得大，因此不必在渲染阴影时指定 Depth bias ，这样也能规避掉 Peter Panning 。

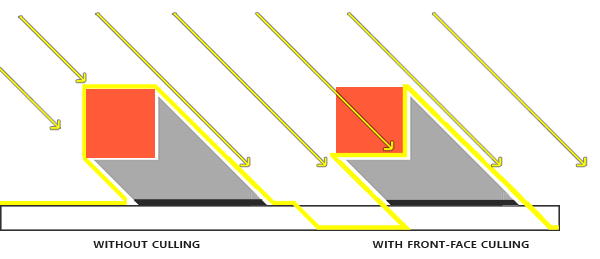
然而这个做法并不是一劳永逸的，首先它只能应用于实心物体（Water-tight），对于透明或中间开洞的物体无法应用，对于地板之类的单平面也无法应用，同时在精度不够时可能会产生漏光（Light bleeding）的问题。因此最好的方案永远是具体问题具体分析。

精度问题的解决方案：PCF

阴影映射的另一个问题是同样由于阴影贴图分辨率不足所造成的走样，而且物体利光源越远就会越严重，如下图所示的锯齿状瑕疵：

一个常用于解决阴影映射的走样问题的方案是百分比渐进过滤（Percentage closer filtering，PCF），和通常的反走样方法类似，PCF同样是利用更多的采样点，去平滑/模糊生硬的锯齿边缘。

正如PCF的名字所言，“百分比”渐进过滤：之前在做阴影映射时，我们的shadowFactor是非0即1（当处于阴影中时是0，否则是1），这就代表片元要么完全处于阴影当中，要么完全不被阴影遮挡；而应用了PCF后，我们的shadowFactor就变为了[0,1]区间内的一个小数值，有了类似软阴影的效果，用shadowFactor乘上输出的片元color，就能得到平滑过渡的阴影边缘。

PCF的具体做法：在采样阴影贴图时对于目标采样点的周围同样进行采样，将得到的所有结果进行加权平均，并且采样点数量越多模糊半径越大，带来的开销也就越大。

$$V(x)=\sum_{q\in\mathcal{N}(p)}w(p,q)\cdot\chi^+[D_{SM}(q)-D_{scene}(x)]$$

该PCF公式中，自变量 $x$ 表示当前片元，$p$ 表示当前片元对应的采样点，$\mathcal{N}(p)$ 表示采样点 $p$ 附近的点，$w(p,q)$ 表示权重，$D_{SM}(q)$ 表示在 $q$ 处采样阴影贴图得到的深度，$D_{scene}(x)$ 表示当前片元的深度，$\chi^+$ 在此处指的是一个非0即1的符号函数。

以下HLSL代码演示了一个无加权的9核PCF实现方法：

//HLSL
shadowMap.GetDimensions(0, width, height, numMips);
float dx = 1.0 / (float)width;

const float2 offsets[9] = {
    float2(-dx, -dx), float2(0.0, -dx), float2(dx, -dx),
    float2(-dx, 0.0), float2(0.0, 0.0), float2(dx, 0.0),
    float2(-dx, dx), float2(0, dx), float2(dx, dx)
};

float percentLit = 0.0;

for (int i = 0; i < 9; i++)
    percentLit += shadowMap.SampleCmp(
        samplerComparison, 
        shadowPosition.xy + offsets[i], 
        currentDepth).r;

percentLit /= 9.0;

PCF最初被发明出来的功用就是实现阴影映射反走样，但是人们发现它可以达到类似软阴影的效果，因此便在其上提出了PCSS算法，这就是我们接下来要讨论的话题。

从硬阴影到软阴影：PCSS

软阴影基本原理

硬阴影是用传统的阴影映射的方法绘制出来的，但在现实生活中我们遇到的大部分是软阴影，以下两图比较，我们会很自然地觉得软阴影更加真实。

通过观察我们可以发现，阴影的模糊程度是与光源和物体的距离，物体和阴影投射面的距离相关的，可以简单将其总结为以下相似三角形：

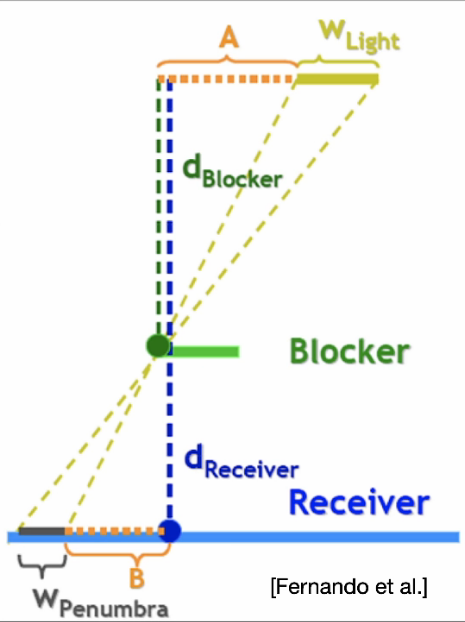
该图中 $w_{Light}$ 表示区域光源的大小，$w_{Penumbra}$ 表示半阴影区域的大小，$d_{Blocker}$ 表示光源到遮挡物的距离，$d_{Receiver}$ 表示光源到投影面的距离。

该相似三角形的数学表述如下：

$$w_{Penumbra}=(d_{Receiver}-d_{Blocker})\frac{w_{Light}}{d_{Blocker}}$$

很明显，这与我们的观察相符，即光源离遮挡物和投影面距离越远阴影越小，遮挡物离投影面距离越远阴影越模糊（半阴影区域越大）。

PCSS

前面我们提到过PCF可以做到模糊阴影的效果，这使它成为了实现软阴影的不二之选，衍生出的方法名为百分比渐进软阴影（Percentage closer soft shadow，PCSS），它由Fernando在2005年提出。

实现PCSS的方法可以拆分为以下几个基本流程：

1. 找到形成阴影的遮挡物并计算对应深度（一般取平均深度）。
2. 根据 $d_{Blocker}$ 和已有数据，计算出 $w_{Penumbra}$ 。
3. 实施PCF。

首先我们需要找到形成阴影的遮挡物，一个常规的思路是将片元处与区域光源处处相连（可以看作一个视锥体），查找是否有其它的物体挡在这些连线中，要做到这点只需要根据连线采样阴影贴图即可。

可以将阴影贴图视作处在光源视角的近平面上，nearZ视作阴影贴图的深度，nearWidth视作阴影贴图的宽度。

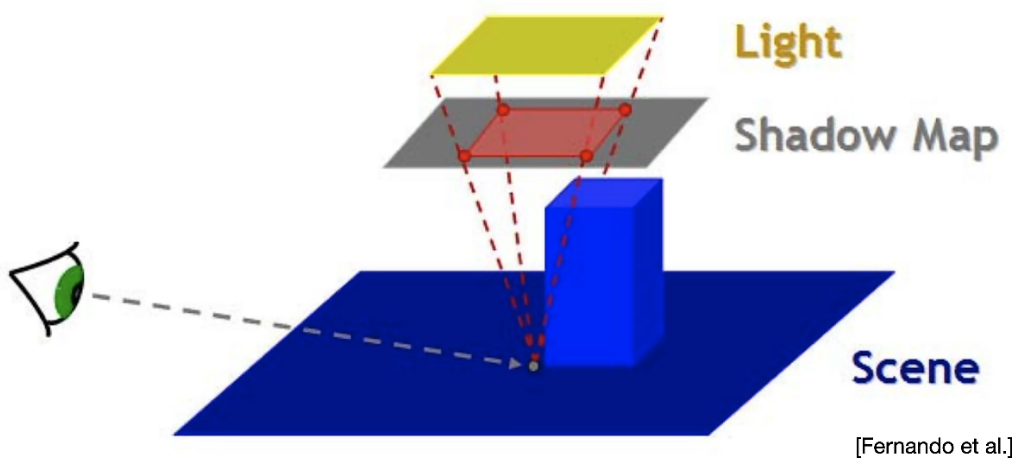
可以看出，指定的区域光源越大，需要的阴影贴图采样点也就越多，开销会更大。

在找出所有的遮挡物后完成平均深度的计算。参考以下HLSL代码：

//HLSL
float searchWidth = (currentDepth - nearZ) / currentDepth * lightWidth;
float sampleWidth = searchWidth / nearWidth;

uint sampleCount = 0;

for (float i = -sampleWidth / 2.0; i < sampleWidth / 2.0; i += step) {
    for (float j = -sampleWidth / 2.0; j < sampleWidth / 2.0; j += step) {
        float2 offset = float2(i, j);
        float sampleDepth = shadowMap.Sample(sampler, shadowPosition.xy + offset).r;

        if(currentDepth > sampleDepth) {
            blockerDepth += sampleDepth;
            sampleCount++;
        }
    }
}

blockerDepth /= sampleCount;

接下来完成 $w_{Penumbra}$ 的计算，参考以下HLSL代码：

//HLSL
float w = (currentDepth - blockerDepth) / blockerDepth * lightWidth;
float pcfRadius = w / nearWidth / 2.0;

最后根据计算出的pcfRadius，实施PCF：

//HLSL
uint sampleCount = 0;

for (float i = -pcfRadius; i < pcfRadius; i += step) {
    for (float j = -pcfRadius; j < pcfRadius; j += step) {
        float2 offset = float2(i, j);

        percentLit += shadowMap.SampleCmp(
            samplerComparison, 
            shadowPosition.xy + offset, 
            currentDepth).r;

        sampleCount++;
    }
}

percentLit /= sampleCount;

可以看出，在PCSS中我们使用了两步采样，这会造成较大的开销，对于实时渲染是不友好的。一个节省开销的方法是减少采样次数，在需要采样的区域中随机稀疏抽样，这当然会造成噪点，但是通过降噪算法可以达到比较好的效果，这也是工业界中最常用的做法。

GPU Pro 6 中提出了一种节省采样开销的办法，名为接触硬化阴影（Contact hardening shadow，CHS），它的思路是利用阴影贴图的Mipmaps，因为现代图形API提供了对生成Mipmaps的硬件支持，因此可以将开销降到最低。在进行PCF时，对于硬阴影采样分辨率较高的Mipmap层级，对于软阴影采样分辨率较低的Mipmap层级。CHS还有更多的衍生方法，比如分离软阴影映射（Separable soft shadow mapping，SSSM），这里不作过多讲解。

另一个利用到Mipmaps的方法是 Hierarchical min/max shadow map，该方法创建两个Mipmap层级，一个存储指定区域内的最大深度值（Hierarchical-Z，HiZ），一个存储最小深度值，这样可以快速判断片元是否处于全阴影中，避免不必要的采样。例如若片元的深度在一定区域内大于Mipmap中存储的最大深度值，那么就可以认为该片元完全处于阴影中。

优化：概率近似方法 VSM

Donnelly, William, Andrew Lauritzen 在2006年首次提出方差阴影映射（Variance shadow mapping，VSM），这是一个用到很多概率计算和近似估计的PCSS优化方案，因此是完全不具有物理正确性的，但是却能用较低的开销取得较好的效果，因此在实时渲染中拥有一席之地。

均值和方差

VSM要求对深度数据计算均值和方差，均值的计算方式主要有以下两种：

1. 为阴影贴图生成Mipmaps，因为高层级Mipmap是对低层级Mipmap的插值，因此可以起到计算平均值的作用。
2. 使用前缀和算法生成SAT（Summed area tables，求和面积表），利用SAT计算平均值。

这两种方法各有各的优缺点：Mipmaps的优点是有GPU硬件支持，速度较快，缺点是太过不精确；SAT的优点是较为精确，缺点则是在不使用并行计算的情况下速度太慢。

Mipmaps方法不必多说，简单介绍一下SAT方法的实现过程：

SAT是前缀和算法的一个衍生数据结构，常用于图像处理中，使用SAT需要和源图像相同分辨率的一张图像（可以考虑存储在另一个通道中）。首先对源图像每行进行一维前缀和（即对数值进行逐个累加，将累加后得到的数值记在当前位置），在计算完成后再对每列计算一维前缀和。

计算一维前缀和的过程可以使用并行计算加速，图像分辨率越高能节省的开销越大。

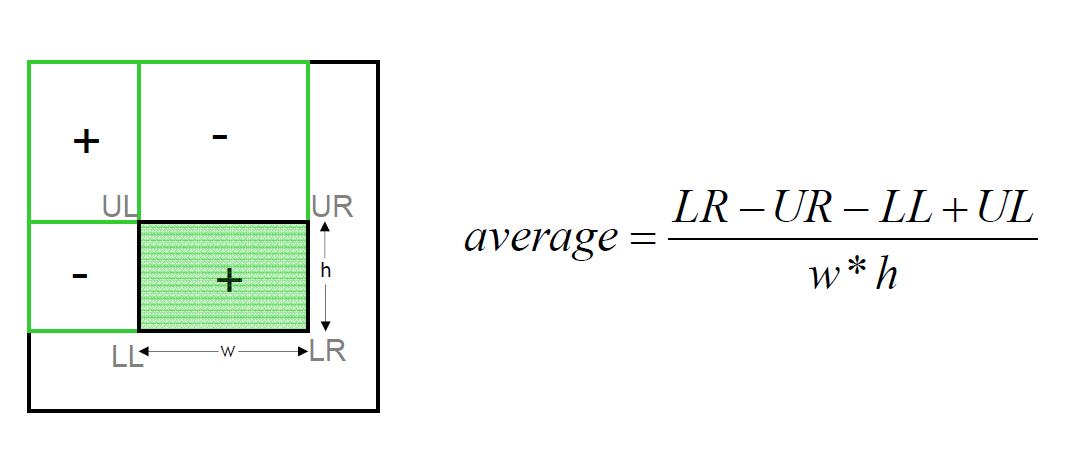
在SAT中的每一个位置记录的数值，都是源图像从左上角一直到该位置的数值和，因此可以任意取出一定范围内的数值和，然后再根据范围的大小求平均即可。

VSM计算方差用到了概率论中的方差均值公式：

$$Var(X)=E(X^2)-E^2(X)$$

为了计算方差，我们还需要在生成阴影贴图时额外生成一张平方阴影贴图，即图像中的深度值都是原阴影贴图的平方。

参考以下HLSL代码：

//HLSL
float sum = shadowMap.Sample(sampler, shadowPosition.xy + float2(radius, radius))
    - shadowMap.Sample(sampler, shadowPosition.xy + float2(-radius, radius))
    - shadowMap.Sample(sampler, shadowPosition.xy + float2(radius, -radius))
    + shadowMap.Sample(sampler, shadowPosition.xy + float2(-radius, -radius));

float sumSquared = squaredShadowMap.Sample(sampler, shadowPosition.xy + float2(radius, radius))
    - squaredShadowMap.Sample(sampler, shadowPosition.xy + float2(-radius, radius))
    - squaredShadowMap.Sample(sampler, shadowPosition.xy + float2(radius, -radius))
    + squaredShadowMap.Sample(sampler, shadowPosition.xy + float2(-radius, -radius));

float size = radius * radius;
float variance = sumSquared / size - sum / size;

切比雪夫不等式

切比雪夫不等式（Chebyshev’s inequality） 是概率论中一个重要的公式，它可以根据均值和方差，在一定程度上告诉我们随机变量的分布概率，此处我们使用的是它的单边形式：

$$P(x>t)\leq\frac{\sigma^2}{\sigma^2+(t-\mu)^2}\quad (t>\mu)$$

该公式中，$\mu$ 表示均值，$\sigma^2$ 表示方差。

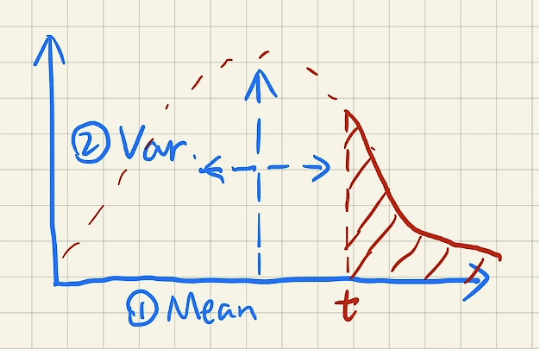
在VSM中，我们一般直接将切比雪夫不等式中的不等号看作约等号使用。

切比雪夫不等式在一定程度上可以当作PCF的低开销近似方法，因为PCF本身就是在查询一定范围内 $x>t$ 的采样点数量，而切比雪夫不等式从概率层面解决了这个问题：

$$V(x)\approx P(x>t)$$

参考以下HLSL代码：

//HLSL
float probability = variance / (variance + pow((currentDepth - average), 2.0));

由于切比雪夫不等式的界并不紧密，一些该处于全阴影中的区域会错误地发亮，即产生漏光问题，可以通过设置截断一定程度上缓解这个问题（毕竟比起漏光，我们宁愿阴影更黑一点）。

具体做法是设置一个阈值threshold，当计算出的 $P(x>t)$ 位于 [0,threshold] 区间中时，就将 $P(x>t)$ 截断为0，并将 [threshold,1] 重新映射至 [0,1] 区间，参考以下HLSL代码：

//HLSL
probability = saturate((probability - threshold) / (1.0 - threshold));

新的遮挡物深度计算方案

回到PCSS的步骤，在查找遮挡物时，我们首先要比较采样出的深度和当前片元的深度，再把确实是遮挡物的深度做平均，这就太过繁琐了。实际上，根据遮挡物深度和平均深度的关系，我们可以写出下面这个等式：

$$\frac{N_1}{N}z_{unocc}+\frac{N_2}{N}z_{occ}=z_{avg}$$

这个等式的意思是：遮挡物的平均深度和非遮挡物的平均深度根据各自所占比例做加权平均，就能得到平均深度。

接下来我们要用到切比雪夫不等式去做第一个近似：

$$\begin{aligned}\frac{N_1}{N}&\approx P(x>t)\\ \frac{N_2}{N}&\approx 1-P(x>t)\end{aligned}$$

要求得 $z_{occ}$ ，我们还需要知道 $z_{unocc}$ ，因此我们需要做第二个近似：假设非遮挡物得深度都和当前片元深度相同，即

$$z_{unocc}\approx t$$

这个假设同样是很不准确的，我们会遇到和阴影粉刺类似的问题。

由此，我们就可以计算出遮挡物平均深度，参考以下HLSL代码：

//HLSL
float sampleDepth = shadowMap.Sample(sampler, shadowPosition.xy);
float unoccDepth = sampleDepth;

float probability = variance / (variance + pow((sampleDepth - average), 2.0));
float blockerDepth = (average - probability * sampleDepth) / (1.0 - probability);

由此，我们将原本开销很大的多次采样减少到了只剩一次采样。

更多Prefilter阴影映射

VSM通过切比雪夫不等式来降低采样次数，大大节省了开销，但这本身是极不精确的，而且这样模拟出的分布函数往往和真实的深度分布有一定的差距，在一些极端情况下，这种差距会被加重，从而导致阴影明暗分布不正常，甚至出现漏光的现象等。

下面简单介绍几个VSM的代替方案，它们和VSM一样都有各自的优缺点，没有一种方法能保证完全解决所有问题，在实际应用中要权衡利弊。

指数阴影映射 ESM

指数函数被认为也能不错地模拟深度分布，而且可以使用参数调控

矩阴影映射 MSM

有一个能保证更准确的深度分布的阴影方案，称作矩阴影映射（Moment shadow mapping，MSM），即使用更高阶的矩（标准差）在最大程度上确保信息不会丢失，通常最低需要四阶矩。MSM需要的存储量较大，将32位浮点数存储改为16位浮点数存储可以节省一些内存。

MSM的数学推导过程十分复杂，在实际工程中应用也不是很广泛，因此我们不会在这过多解释，简单了解即可。

级联阴影 CSM