数学分析初步（六）：无穷级数与常微分方程

数项级数

数项级数的概念与性质

设 $\{ u_0 \}$ 是一个无穷数列，则称式子

$$\sum_{n = 1}^\infty u_n = u_1 + u_2 + \cdots + u_n + \cdots$$

为数项级数。其中数 $u_n$ 称为级数的第 $n$ 项，也称为一般项；级数前 $n$ 项和 $S_n = u_1 + u_2 + \cdots + u_n$ 称为第 $n$ 次部分和，数列 $S_1, S_2, \cdots, S_n$ 称为级数的部分和数列，简记为 $\{ S_n \}$.

级数的敛散性： 如果当 $n \to \infty$ 时，级数的部分和数列 $\{ S_n \}$ 的极限存在，即

$$\lim_{n \to \infty} S_n = s$$

则称该级数收敛，其和为 $s$；否则称该级数发散。

数项级数的性质：

1. 设 $\sum\limits_{n = 1}^\infty u_n = s$，$\sum\limits_{n = 1}^\infty v_n = \sigma$，则 $\sum\limits_{n = 1}^\infty (u_n \pm v_n) = s \pm \sigma$.
2. 设 $\sum\limits_{n = 1}^\infty u_n = s$，则 $\sum\limits_{n = 1}^\infty au_n = as\ (a \neq 0)$.
3. 在一个级数前加上或去掉有限项，级数的敛散性不会发生改变。
4. 在收敛数列中任意加上括号，既不改变其敛散性，也不改变其和。
5. 级数 $\sum\limits_{n = 1}^\infty u_n$ 收敛的必要条件是 $\lim\limits_{n \to \infty} u_n = 0$.

例：讨论几何级数

$$\sum_{n = 0}^\infty q^n = 1 + q + q^2 + \cdots + q^n + \cdots$$

的敛散性。

解：该级数的部分和为

$$S_n = \begin{cases} \dfrac{(1 - q^n)}{1 - q}, & q \neq 1 \\ n, & q = 1 \end{cases}$$

当 $|q| < 1$ 时，$\lim\limits_{n \to \infty} S_n = \dfrac{1}{1 - q}$，故级数收敛，且和为 $\dfrac{1}{1 - q}$；

当 $|q| \geq 1$ 时，$\lim\limits_{n \to \infty} S_n$ 不存在，故级数发散。

定理： 各项倒数为等差数列的级数，称作调和级数，是一个发散的无穷级数。

例：证明调和级数

$$\sum_{n = 1}^\infty\dfrac{1}{n} = 1 + \dfrac{1}{2} + \dfrac{1}{3} + \cdots + \dfrac{1}{n} + \cdots$$

是发散的。

解：反证法。假设该级数收敛，则对其部分和有 $\lim\limits_{n \to \infty} S_n = s$，同理也有 $\lim\limits_{n \to \infty} S_{2n} = s$，于是

$$\lim_{n \to \infty} (S_{2n} - S_n) = s - s = 0$$

但另一方面，有

$$S_{2n} - S_n = \frac{1}{n + 1} + \frac{1}{n + 2} + \cdots + \frac{1}{2n} > \frac{1}{2n} + \frac{1}{2n} + \cdots + \frac{1}{2n} = \frac{1}{2}$$

产生矛盾，所以上述假设不成立，该级数发散。

定理： 若级数 $\sum\limits_{n = 1}^\infty u_n$ 收敛，则级数 $\sum\limits_{n = 1}^\infty u_n + u_{n + 1}$ 必收敛。

证明：设级数 $\sum\limits_{n = 1}^\infty u_n$ 的和为 $s$，$\sum\limits_{n = 1}^\infty u_n + u_{n + 1}$ 的前 $n$ 项和为 $S_n$，则

$$\begin{aligned} S_n &= (u_1 + u_2) + (u_2 + u_3) + \cdots + (u_n + u_{n + 1})\\ &= u_1 + 2(u_2 + \cdots + u_n) + u_{n + 1}\\ \lim_{n \to \infty} S_n &= u_1 + 2(s - u_1) = 2s - u_1 \end{aligned}$$

故级数 $\sum\limits_{n = 1}^\infty u_n + u_{n + 1}$ 收敛，和为 $2s - u_1$.

正项级数的敛散性

若级数 $\sum\limits_{n = 1}^\infty u_n$ 的各项都是非负的，则称 $\sum\limits_{n = 1}^\infty u_n$ 为正项级数。正项级数收敛的充要条件是它的部分和数列 $\{ S_n \}$ 有上界。

比较判别法： 设 $\sum\limits_{n = 1}^\infty u_n$ 和 $\sum\limits_{n = 1}^\infty v_n$ 都是正项级数，且 $u_n \leq v_n$. 若级数 $\sum\limits_{n = 1}^\infty v_n$ 收敛，则级数 $\sum\limits_{n = 1}^\infty u_n$ 也收敛；反之，若级数 $\sum\limits_{n = 1}^\infty u_n$ 发散，则级数 $\sum\limits_{n = 1}^\infty v_n$ 也发散。

推论：

• 若正项级数 $\sum\limits_{n = 1}^\infty v_n$ 收敛，且存在正整数 $N$，当 $n \geq N$ 时有 $u_n \leq kv_n\ (k > 0)$ 成立，则正项级数 $\sum\limits_{n = 1}^\infty u_n$ 收敛；
• 若正项级数 $\sum\limits_{n = 1}^\infty u_n$ 发散，且存在正整数 $N$，当 $n \geq N$ 时有 $ku_n \leq v_n\ (k > 0)$ 成立，则正项级数 $\sum\limits_{n = 1}^\infty v_n$ 发散。

比较判别法的极限形式： 设 $\sum\limits_{n = 1}^\infty u_n$ 和 $\sum\limits_{n = 1}^\infty v_n$ 都是正项级数，$v_n > 0$，且 $\lim\limits_{n \to \infty}\dfrac{u_n}{v_n} = l$，

1. 若 $0 < l < +\infty$，则级数 $\sum\limits_{n = 1}^\infty u_n$ 和 $\sum\limits_{n = 1}^\infty v_n$ 敛散性相同；
2. 若 $l = 0$ 且 $\sum\limits_{n = 1}^\infty v_n$ 收敛，则 $\sum\limits_{n = 1}^\infty u_n$ 也收敛；
3. 若 $l = +\infty$ 且 $\sum\limits_{n = 1}^\infty v_n$ 发散，则 $\sum\limits_{n = 1}^\infty u_n$ 也发散。

例：判断 p 级数（$p > 0$）

$$\sum_{n = 1}^\infty\dfrac{1}{n^p} = 1 + \dfrac{1}{2^p} + \dfrac{1}{3^p} + \cdots + \dfrac{1}{n^p} + \cdots$$

的敛散性。

解：当 $p \leq 1$ 时，满足 $\dfrac{1}{n^p} \geq \dfrac{1}{n}$，使用比较判别法，将其和调和级数作比较，由调和级数发散可知该级数同样发散。

当 $p > 1$ 时，该级数的前 $n$ 项和为

$$\begin{aligned} S_n &= 1 + \left( \frac{1}{2^p} + \frac{1}{3^p} \right) + \left( \frac{1}{4^p} + \cdots + \frac{1}{7^p} \right) + \left( \frac{1}{8^p} + \cdots + \frac{1}{15^p} \right) + \cdots + \frac{1}{n^p}\\ &\leq 1 + \left( \frac{1}{2^p} + \frac{1}{2^p} \right) + \left( \frac{1}{4^p} + \cdots + \frac{1}{4^p} \right) + \left( \frac{1}{8^p} + \cdots + \frac{1}{8^p} \right) + \cdots\\ &+ \underbrace{\left( \frac{1}{(2^l)^p} + \frac{1}{(2^l)^p} + \cdots + \frac{1}{(2^l)^p} \right)}_{2^l}\\ &= 1 + \frac{1}{2^{p - 1}} + \frac{1}{(2^{p - 1})^2} + \cdots + \frac{1}{(2^{p - 1})^l}\\ &= \frac{1 - \left( \dfrac{1}{2^{p - 1}} \right)^{l + 1}}{1 - \dfrac{1}{2^{p - 1}}} < \frac{1}{1 - \dfrac{1}{2^{p - 1}}} \end{aligned}$$

所以 $S_n$ 有界，可得该级数收敛。

比值判别法（D’Alembert 判别法）： 设 $\sum\limits_{n = 1}^\infty u_n$ 为正项级数，$u_n > 0$，且 $\lim\limits_{n \to \infty}\dfrac{u_{n + 1}}{u_n} = \rho$. 则

$$\begin{cases} \rho < 1, & \text{级数收敛}\\ \rho > 1 \ \text{或} \ \lim\limits_{n \to \infty}\dfrac{u_{n + 1}}{u_n} = \infty, & \text{级数发散}\\ \rho = 1, & \text{无法判断} \end{cases}$$

证明：当 $\rho < 1$ 时，取 $q$ 满足 $\rho < q < 1$. 由极限的保号性可知，存在正整数 $N$，当 $n > N$ 时有 $\dfrac{u_{n + 1}}{u_n} < q$，从而

$$u_{N + 2} < qu_{N + 1}, u_{N + 3} < qu_{N + 2} < q^2u_{N + 1}, \cdots, u_{N + m} < q^{m - 1}u_{N + 1}$$

因为级数 $\sum\limits_{m = 1}^\infty q^{m - 1}u_{N + 1}$ 收敛，由比较判别法可知级数 $\sum\limits_{m = 1}^\infty u_{N + m}$ 收敛，从而级数 $\sum\limits_{n = 1}^\infty u_n$ 收敛。

当 $\rho > 1$ 时，由极限的保号性可知，存在正整数 $N$，当 $n > N$ 时有 $\dfrac{u_{n + 1}}{u_n} > 1$，即 $u_{n + 1} > u_n$. 于是 $\lim\limits_{n \to \infty} u_n \neq 0$，从而级数 $\sum\limits_{n = 1}^\infty u_n$ 发散。

例：判别级数 $\sum_{n = 1}^\infty \dfrac{a^n n!}{n^n}\ (a > 0)$ 的敛散性。

解：令 $u_n = \dfrac{a^n n!}{n^n}$，则 $u_n > 0$，且

$$\lim_{n \to \infty} \frac{u_{n + 1}}{u_n} = \lim_{n \to \infty} \frac{a^{n + 1}(n + 1)!}{(n + 1)^{n + 1}} \cdot \frac{n^n}{a^n n!} = \lim_{n \to \infty}\frac{a}{\left( 1 + \dfrac{1}{n} \right)^n} = \frac{a}{e}$$

当 $a < e$ 时，级数 $\sum_{n = 1}^\infty \dfrac{a^n n!}{n^n}$ 收敛；当 $a > e$ 时，级数 $\sum_{n = 1}^\infty \dfrac{a^n n!}{n^n}$ 发散；当 $a = e$ 时，比值判别法失效。

根式判别法（Cauchy 判别法）： 设 $\sum\limits_{n = 1}^\infty u_n$ 为正项级数，且 $\lim\limits_{n \to \infty} \sqrt[n]{u_n} = \rho$，则

$$\begin{cases} \rho < 1, & \text{级数收敛}\\ \rho > 1, & \text{级数发散}\\ \rho = 1, & \text{无法判断} \end{cases}$$

证明：当 $\rho < 1$ 时，取 $q$ 满足 $\rho < q < 1$. 由极限的保号性可知，存在正整数 $N$，当 $n > N$ 时有 $\sqrt[n]{u_n} < q < 1$，即 $u_n < q^n$.
因为级数 $\sum\limits_{m = 1}^\infty q^n$ 收敛，由比较判别法可知级数 $\sum\limits_{n = 1}^\infty u_n$ 也收敛。

当 $\rho > 1$ 时，由极限的保号性可知，存在正整数 $N$，当 $n > N$ 时有 $\sqrt[n]{u_n} > 1$，即 $u_n > 1$. 于是 $\lim\limits_{n \to \infty} u_n \neq 0$，从而级数 $\sum\limits_{n = 1}^\infty u_n$ 发散。

当 $\rho = 1$ 时，以 p 级数为例，有

$$\sqrt[n]{u_n} = \left( \frac{1}{\sqrt[n]{n}} \right)^p \to 1 \quad (n \to \infty)$$

说明当 $\rho = 1$ 时，级数敛散性不定。

积分判别法： 设 $f(x)$ 是半轴 $x \geq 1$ 上的非负递减函数，且 $f(n) = u_n$，则级数 $\sum\limits_{n = 1}^\infty u_n$ 收敛的充要条件是无穷积分 $\displaystyle\int_1^{+\infty} f(x)\mathrm{d}x$ 收敛。

例：判别级数 $\sum\limits_{n = 2}^\infty \dfrac{1}{n(\ln n)^p}$ 的敛散性。

解：当 $p \leq 0$ 时，由于

$$\lim_{n \to \infty} \frac{\dfrac{1}{n(\ln n)^p}}{\dfrac{1}{n}} = \lim_{n \to \infty} (\ln n)^{-p} = +\infty$$

而级数 $\sum\limits_{n = 1}^\infty \dfrac{1}{n}$ 发散，由比较判别法的极限形式可知，级数 $\sum\limits_{n = 2}^\infty \dfrac{1}{n(\ln n)^p}$ 发散。

当 $p > 0$，$x \geq 2$ 时，取 $f(x) = \dfrac{1}{x(\ln x)^p}$，则级数与无穷积分 $\displaystyle\int_2^{+\infty} \frac{1}{x(\ln x)^p}\mathrm{d}x$ 具有相同的敛散性，而积分

$$\int_2^{+\infty} \frac{1}{x(\ln x)^p}\mathrm{d}x = \int_2^{+\infty}\frac{1}{(\ln x)^p}\mathrm{d}(\ln x) = \int_{\ln 2}^{+\infty} \frac{1}{y^p}\mathrm{d}y$$

当 $p > 1$ 时积分收敛，级数也同样收敛；当 $p \leq 1$ 时积分发散，级数也同样发散。

任意项级数的敛散性

柯西（Cauchy）收敛准则： 数项级数 $\sum\limits_{n = 1}^\infty u_n$ 收敛的充要条件是：$\forall \varepsilon > 0$，$\exists$ 正整数 $N$，当 $n > N$ 时，对一切正整数 $p$ 有

$$\left| \sum_{k = n + 1}^{n + p} u_k \right| < \varepsilon$$

即

$$|u_{n + 1} + u_{n + 2} + \cdots + u_{n + p}| < \varepsilon$$

例：利用柯西收敛准则证明级数 $\sum\limits_{k = 1}^\infty \dfrac{1}{k^2}$ 收敛。

证明：

$$\begin{aligned} \sum_{k = n + 1}^{n + p} \frac{1}{k^2} &< \frac{1}{n(n + 1)} + \frac{1}{(n + 1)(n + 2)} + \cdots + \frac{1}{(n + p - 1)(n + p)}\\ &= \left( \frac{1}{n} - \frac{1}{n + 1} \right) + \left( \frac{1}{n + 1} - \frac{1}{n + 2} \right) + \cdots + \left( \frac{1}{n + p - 1} - \frac{1}{n + p} \right)\\ &= \frac{1}{n} - \frac{1}{n + p} < \frac{1}{n} \end{aligned}$$

$\forall \varepsilon > 0$，$\exists N = \left\lfloor \dfrac{1}{\varepsilon} \right\rfloor + 1$，使得当 $n > N$ 且 $p$ 为正整数时有

$$\left| \sum_{k = n + 1}^{n + p} \frac{1}{k^2} \right| < \varepsilon$$

由柯西收敛准则可知该级数收敛。

莱布尼茨（Leibniz）判别法： 若交错级数 $\sum\limits_{n = 1}^\infty (-1)^{n + 1} u_n\ (u_n > 0)$ 满足

1. $u_n \geq u_{n + 1}$；
2. $\lim\limits_{n \to \infty} u_n = 0$.

则交错级数 $\sum\limits_{n = 1}^\infty (-1)^{n + 1} u_n$ 收敛。

例：判别级数 $\sum\limits_{n = 1}^\infty \dfrac{(-1)^n}{n - \ln n}$ 的收敛性。

解：因为 $u_n = \dfrac{1}{n - \ln n}$，所以该级数为交错级数。因为

1. $\lim\limits_{n \to \infty} \dfrac{1}{n - \ln n} = \lim\limits_{n \to \infty} \dfrac{1}{n \left( 1 - \dfrac{\ln n}{n} \right)} = 0$.
2. 令 $f(x) = \dfrac{1}{x - \ln x}$，则 $f'(x) = \dfrac{-\left( 1 - \dfrac{1}{x} \right)}{(x - \ln x)^2} = \dfrac{\dfrac{1}{x} - 1}{(x - \ln x)^2}$，当 $x > 1$ 时，$f'(x) < 0$，故 $f(x)$ 为单调递减函数，有 $u_{n + 1} < u_n$.

综上所述，级数 $\sum\limits_{n = 1}^\infty \dfrac{(-1)^n}{n - \ln n}$ 收敛。

绝对收敛与条件收敛：

• 设级数 $\sum\limits_{n = 1}^\infty u_n$，若将其每一项都取绝对值以后得到的级数 $\sum\limits_{n = 1}^\infty |u_n|$ 收敛，则称级数 $\sum\limits_{n = 1}^\infty u_n$ 绝对收敛；
• 若级数 $\sum\limits_{n = 1}^\infty u_n$ 收敛，而级数 $\sum\limits_{n = 1}^\infty |u_n|$ 发散，则称级数 $\sum\limits_{n = 1}^\infty u_n$ 条件收敛。

定理： 若级数 $\sum\limits_{n = 1}^\infty u_n$ 绝对收敛，则级数 $\sum\limits_{n = 1}^\infty u_n$ 必定收敛。

证明：令 $v_n = \dfrac{1}{2}(|u_n| + u_n)$，则 $0 \leq v_n \leq |u_n|$. 又因为级数 $\sum\limits_{n = 1}^\infty |u_n|$ 收敛，故 $\sum\limits_{n = 1}^\infty v_n$ 收敛，因此 $\sum\limits_{n = 1}^\infty u_n$ 收敛。

例：若 $\sum\limits_{n = 0}^\infty a_n x^n$ 在 $x = x_0 \neq 0$ 处收敛，证明在 $|x| < |x_0|$ 内，$\sum\limits_{n = 0}^\infty a_n x^n$ 绝对收敛。

证：因为数项级数 $\sum\limits_{n = 0}^\infty a_n x_0^n$ 收敛，所以 $\lim\limits_{n \to \infty} a_n x_0^n = 0$，从而数列 $\{ a_n x_0^n \}$ 有界，即存在 $M > 0$，使得 $|a_n x_0^n| < M$.

当 $|x| < |x_0|$ 时，由于

$$\left| a_n x^n \right| = \left| a_n x_0^n \left( \frac{x}{x_0} \right)^n \right| < M \left| \frac{x}{x_0} \right|^n$$

且几何级数 $\sum\limits_{n = 0}^\infty \left| \dfrac{x}{x_0} \right|^n$ 收敛，所以 $\sum\limits_{n = 0}^\infty a_n x^n$ 绝对收敛。

函数项级数

函数项级数的基本概念

设区间 $I$ 是函数 $u_n(x) \ (n = 1, 2, \cdots)$ 的公共定义域，则称下式

$$\sum_{n = 1}^\infty u_n(x) = u_1(x) + u_2(x) + \cdots + u_n(x) + \cdots$$

为 $I$ 上的函数项级数。对 $x_0 \in I$，如果数项级数

$$u_1(x_0) + u_2(x_0) + \cdots + u_n(x_0) + \cdots$$

收敛，则称 $x_0$ 为该级数的收敛点，否则称 $x_0$ 为该级数的发散点。级数的所有收敛点组成的集合为级数的收敛域，其发散点的集合称为级数的发散域。

设级数的收敛域为 $I$，对 $I$ 中的每个点 $x_0$，规定

$$S(x)\big|_{x = x_0} = \sum_{n = 1}^\infty u_n(x_0)$$

则 $S(x)$ 是定义在 $I$ 上的函数，称为该级数的和函数，记作

$$S(x) = \sum_{n = 1}^\infty u_n(x)$$

并且级数在 $I$ 上处处收敛于 $S(x)$. 级数的前 $n$ 项和记作 $S_n(x)$，即

$$S_n(x) = \sum_{k = 1}^n u_k(x)$$

$R_n(x) = S(x) - S_n(x) = \sum_{k = n + 1}^\infty u_k(x)$ 称为级数的余项。

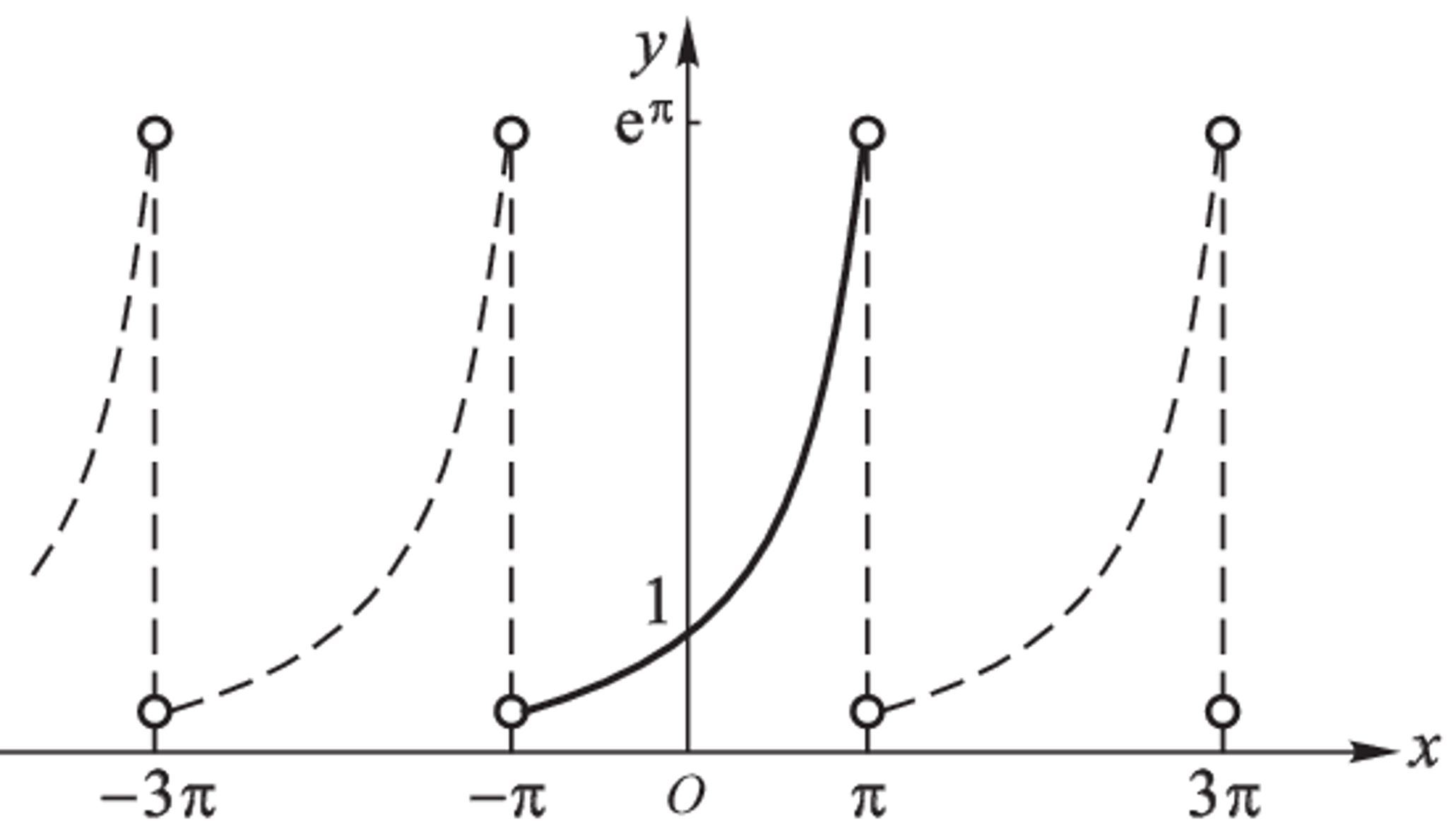
例：求函数项级数

$$\mathrm{e}^{-x} + 2\mathrm{e}^{-2x} + \cdots + n\mathrm{e}^{-nx} + \cdots$$

的收敛域。

解：函数 $u_n(x) = n\mathrm{e}^{-nx}$ 的定义域是区间 $(-\infty, +\infty)$，对每个给定的实数 $x_0$，有数项级数

$$\mathrm{e}^{-x_0} + 2e_{-2x_0} + \cdots + n\mathrm{e}^{-nx_0} + \cdots$$

因为

$$\rho = \lim_{n \to \infty}\frac{(n + 1)\mathrm{e}^{-(n + 1)x_0}}{n\mathrm{e}^{-nx_0}} = \mathrm{e}^{-x_0}$$

所以由比值判别法可得：

1. 当 $x_0 > 0$ 时，$\rho < 1$，级数收敛；
2. 当 $x_0 < 0$ 时，$\rho > 1$，级数发散；
3. 当 $x_0 = 0$ 时，级数为 $1 + 2 + 3 + \cdots + n + \cdots$，它是发散的。

综上所述，该级数的收敛域为区间 $(0, +\infty)$.

函数项级数的一致收敛性

设 $s(x)$ 是定义在 $I$ 上的函数，若 $\forall\varepsilon > 0$，则存在正整数 $N(\varepsilon)$，使得当 $n > N$ 时，对 $\forall x \in I$，都有

$$\left| \sum_{k = 1}^n u_k(x) - s(x) \right| < \varepsilon$$

则称级数 $\sum\limits_{n = 1}^\infty u_n(x)$ 在 $I$ 上一致收敛于 $s(x)$.

柯西（Cauchy）收敛准则： 级数 $\sum\limits_{n = 1}^\infty u_n(x)$ 在 $I$ 上一致收敛的充要条件是：$\forall\varepsilon > 0$，存在正整数 $N(\varepsilon)$，当 $n > N$ 时，对一切正整数 $p$ 和 $\forall x \in I$，都有

$$|S_{n + p}(x) - S_n(x)| = \left| \sum_{k = n + 1}^{n + p} u_k(x) \right| < \varepsilon$$

M 判别法（Weierstrass 判别法）： 设正项级数 $\sum\limits_{n = 1}^\infty M_n$ 收敛，若对 $\forall x \in I$，都有

$$|u_n(x)| \leq M_n$$

则函数项级数 $\sum\limits_{n = 1}^\infty u_n(x)$ 在 $I$ 上一致收敛。称数项级数 $\sum\limits_{n = 1}^\infty M_n$ 为函数项级数 $\sum\limits_{n = 1}^\infty u_n(x)$ 的强级数。

一致收敛数的和函数的性质：

例：函数项级数 $x + \sum\limits_{n = 1}^\infty(x^{n + 1} - x^n)$ 的第 $n$ 次部分和为

$$S_n(x) = x^n$$

由此可见，当且仅当 $x \in (-1, 1]$ 时，极限 $\lim\limits_{n \to \infty}S_n(x)$ 存在，且

$$\lim_{n \to \infty} S_n(x) = \begin{cases} 0, & x \in (-1, 1) \\ 1, & x = 1 \end{cases}$$

和函数的连续性： 设 $u_n(x)\ (n = 1, 2, \cdots)$ 在 $I$ 上都连续，若函数项级数 $\sum\limits_{n = 1}^\infty u_n(x)$ 在 $I$ 上一致收敛，则其和函数 $S(x)$ 在 $I$ 上也连续。

和函数的可积性： 设 $u_n(x)\ (n = 1, 2, \cdots)$ 在 $[a, b]$ 上都连续，若函数项级数 $\sum\limits_{n = 1}^\infty u_n(x)$ 在 $[a, b]$ 上一致收敛，则其和函数 $S(x)$ 在 $[a, b]$ 上可积，且

$$\int_a^b S(x)\mathrm{d}x = \int_a^b \sum_{n = 1}^\infty u_n(x)\mathrm{d}x = \sum_{n = 1}^\infty \int_a^b u_n(x)\mathrm{d}x$$

和函数的可微性： 设 $u_n(x)\ (n = 1, 2, \cdots)$ 在 $I$ 上都有连续导数，若函数项级数 $\sum\limits_{n = 1}^\infty u_n(x)$ 在 $I$ 上处处收敛于 $S(x)$，且 $\sum\limits_{n = 1}^\infty u_n'(x)$ 在 $I$ 上一致收敛，则和函数 $S(x)$ 在 $I$ 上可导，且

$$S'(x) = \sum_{n = 1}^\infty u_n'(x)$$

幂级数的概念与性质

形如

$$a_0 + a_1(x - x_0) + a_2(x - x_0)^2 + \cdots + a_n(x - x_0)^n + \cdots$$

的函数项级数，称为在点 $x_0$ 的幂级数。当 $x_0 = 0$ 时，有在点 $x = 0$ 处的幂函数为

$$a_0 + a_1x + a_2x^2 + \cdots + a_nx^n + \cdots$$

阿贝尔（Abel）定理： 若级数在 $x = \overline{x}\ (\overline{x} \neq 0)$ 处收敛，则对满足不等式 $|x| < |\overline{x}|$ 的任意 $x$，幂级数绝对收敛；反之，若级数在 $x = \overline{x}$ 处发散，则对满足不等式 $|x| > |\overline{x}|$ 的任意 $x$，幂级数发散。

由阿贝尔定理可知，幂级数的收敛域就是以原点为中心的区间，若将区间的长度表示为 $2R$，则称 $R$ 为幂级数的收敛半径，称 $(-R, R)$ 为幂级数的收敛区间（不包括端点）。

定理： 如果 $\lim\limits_{n \to \infty}\left| \dfrac{a_{n + 1}}{a_n} \right| = \rho$ 或 $\lim\limits_{n \to \infty}\sqrt[n]{|a_n|} = \rho$，则幂级数的收敛半径满足

$$R = \begin{cases} \dfrac{1}{\rho}, & 0 < \rho < +\infty \\ 0, & \rho = +\infty \\ +\infty, & \rho = 0 \end{cases}$$

例：求幂级数 $\sum\limits_{n = 1}^\infty \dfrac{(x + 1)^n}{2^n \cdot n}$ 的收敛区间与收敛域。

解：令 $t = x + 1$，则原级数可以写成 $\sum\limits_{n = 1}^\infty \dfrac{t^n}{2^n \cdot n}$，因为

$$\rho = \lim\limits_{n \to \infty}\left| \frac{a_{n + 1}}{a_n} \right| = \lim_{n \to \infty}\frac{2^n \cdot n}{2^{n + 1}(n + 1)} = \frac{1}{2}$$

所以收敛半径 $R = 2$.

接下来对端点的敛散性进行判断：
当 $t = 2$ 时，$\sum\limits_{n = 1}^\infty \dfrac{t^n}{2^n \cdot n} = \sum\limits_{n = 1}^\infty\dfrac{1}{n}$，级数发散；
当 $t = -2$ 时，$\sum\limits_{n = 1}^\infty \dfrac{t^n}{2^n \cdot n} = \sum\limits_{n = 1}^\infty\dfrac{(-1)^n}{n}$，级数收敛。

综上所述，原级数的收敛区间为 $(-3, 1)$，收敛域为 $[-3, 1)$.

幂级数的代数运算： 设幂级数 $\sum\limits_{n = 0}^\infty a_n x^n$ 和 $\sum\limits_{n = 0}^\infty b_n x^n$ 的收敛半径分别为 $R_1$ 和 $R_2$，并令 $R = \min\{ R_1, R_2 \}$，则在 $(-R, R)$ 内有

• 加法运算：

$$\left( \sum_{n = 0}^\infty a_n x^n \right) \pm \left( \sum_{n = 0}^\infty b_n x^n \right) = \sum_{n = 0}^\infty (a_n \pm b_n)x^n$$

• 乘法运算：

$$\left( \sum_{n = 0}^\infty a_n x^n \right) \cdot \left( \sum_{n = 0}^\infty b_n x^n \right) = \sum_{n = 0}^\infty c_n x^n, \quad c_n = \sum_{k = 0}^n a_k b_{n - k}$$

幂级数的分析运算： 设幂级数 $\sum\limits_{n = 0}^\infty a_n x^n$ 的收敛半径为 $R$，和函数为 $S(n)$，则

• $S(x)$ 在收敛区间 $(-R, R)$ 内连续；如果幂级数在点 $x = R$（或 $x = -R$）处收敛，则 $S(x)$ 在 $x = R$ 处左连续（或在 $x = -R$ 处右连续）。

• $S(x)$ 在收敛区间 $(-R, R)$ 内可微，且可逐项求导，求导后的幂级数与原级数的收敛半径相同：

$$S'(x) = \left( \sum_{n = 0}^\infty a_n x^n \right)' = \sum_{n = 1}^\infty n a_n x^{n - 1}$$

• $S(x)$ 在收敛区间 $(-R, R)$ 内可积，且可逐项求积分，求积分后的幂级数与原级数的收敛半径相同：

$$\int_0^x S(t)\mathrm{d}t = \int_0^x \left( \sum_{n = 0}^\infty a_n t^n \right)\mathrm{d}t = \sum_{n = 0}^\infty \int_0^x a_n t^n \mathrm{d}t = \sum_{n = 0}^\infty \frac{a_n}{n + 1} x^{n + 1}$$

例：求 $\sum\limits_{n = 1}^\infty \dfrac{x^n}{n}$ 的和函数。

解：因为

$$\lim_{n \to \infty} \frac{n}{n + 1} = 1$$

所以该幂函数的收敛半径为 $1$，设其在 $(-1, 1)$ 内的和函数为 $S(x)$，于是当 $|x| < 1$ 时，有

$$\begin{aligned} S(x) &= \sum_{n = 1}^\infty \frac{x^n}{n} = \sum_{n = 1}^\infty \int_0^x \left( \frac{t^n}{n} \right)'\mathrm{d}t\\ &= \int_0^x \sum_{n = 1}^\infty \left( \frac{t^n}{n} \right)'\mathrm{d}t = \int_0^x \left( \sum_{n = 0}^\infty t^n \right)\mathrm{d}t\\ &= \int_0^x \frac{\mathrm{d}t}{1 - t} = -\ln(1 - x) \end{aligned}$$

因为该幂级数在 $x = -1$ 处收敛，从而

$$\sum_{n = 1}^\infty \frac{x^n}{n}\bigg|_{x = -1} = \lim_{x \to -1^+}\sum_{n = 1}^\infty \frac{x^n}{n} = \lim_{x \to -1^+}[-\ln(1 - x)] = -\ln 2$$

故

$$\sum_{n = 1}^\infty \frac{x^n}{n} = -\ln(1 - x) \quad (-1 \leq x < 1)$$

函数展开成幂级数

如果存在 $R > 0$，使得当 $|x - x_0| < R$ 时，有

$$f(x) = a_0 + a_1(x - x_0) + a_2(x - x_0)^2 + \cdots + a_n(x - x_0)^n + \cdots$$

则称该式为函数 $f(x)$ 在点 $x = x_0$ 处的幂级数展开式。

函数展开成幂级数的必要条件： 如果在 $|x - x_0| < R$ 内上幂级数展开式成立，则有

1. $f(x)$ 在 $|x - x_0| < R$ 内具有任意阶导数；
2. $f(x)$ 在点 $x = x_0$ 处的幂级数展开式就是

$$\begin{aligned} f(x) = & f(x_0) + f'(x_0)(x - x_0) + \frac{1}{2!}f''(x_0)(x - x_0)^2 + \cdots\\ & + \frac{1}{n!}f^{(n)}(x_0)(x - x_0)^n + \cdots \end{aligned}$$

称上式右端的幂级数为 $f(x)$ 在点 $x = x_0$ 处的泰勒级数。当 $x_0 = 0$ 时，上式可以写成

$$f(x) = f(0) + f'(0)x + \frac{1}{2!}f''(0)x^2 + \cdots + \frac{1}{n!}f^{(n)}(0)x^n + \cdots$$

此时上式右端的幂级数又称为 $f(x)$ 的麦克劳林级数。

函数展开成幂级数的充分条件： 若 $f(x)$ 在点 $x = x_0$ 的邻域内具有 $n + 1$ 阶导数，则有‘

$$f(x) = \sum_{k = 0}^n \frac{f^{(k)}(x_0)}{k!}(x - x_0)^k + R_n(x)$$

其中 $R_n(x)$ 为余项。

假设存在 $R > 0$，使得 $f(x)$ 在 $|x - x_0| < R$ 内具有任意阶导数。当 $|x - x_0| < R$ 时，若有

$$\lim_{n \to \infty} R_n(x) = \lim\limits_{n \to \infty}\left[ f(x) - \sum_{k = 0}^n \frac{f^{(k)}(x_0)}{k!}(x - x_0)^k \right] = 0$$

则 $f(x)$ 可展开成泰勒级数。

结论： 设 $f(x)$ 在点 $x_0$ 处的一邻域内具有任意阶导数，并且存在 $R > 0$，使得当 $|x - x_0| < R$ 时，有 $\lim\limits_{n \to \infty} R_n(x) = 0$，则在 $|x - x_0| < R$ 内，$f(x)$ 可展开成泰勒级数。

初等函数的幂级数展开式： （大部分和对应的麦克劳林展开式相同）

（1）$\mathrm{e}^x = 1 + x + \dfrac{1}{2!}x^2 + \cdots + \dfrac{1}{n!}x^n + \cdots$

直接法：因为 $f^{(n)}(0) = 1, f^{(n)}(x) = \mathrm{e}^x\ (n = 0, 1, 2, \cdots)$，所以当 $x \in (-\infty, +\infty)$ 时，有

$$\mathrm{e}^x = 1 + x + \dfrac{1}{2!}x^2 + \cdots + \dfrac{1}{n!}x^n + R_n(x)\\ R_n(x) = \frac{\mathrm{e}^{\theta x}}{(n + 1)!}x^{n + 1} \quad (0 < \theta < 1)$$

对每个固定的 $x \in (-\infty, +\infty)$，有

$$\lim_{n \to \infty} R_n(x) = \lim_{n \to \infty} \frac{\mathrm{e}^{\theta x}}{(n + 1)!}x^{n + 1} = 0$$

（2）$\sin{x} = x - \dfrac{1}{3!}x^3 + \dfrac{1}{5!}x^5 - \cdots + (-1)^{n-1}\dfrac{1}{(2n - 1)!}x^{2n - 1} + \cdots$

直接法：当 $x \in (-\infty, +\infty)$ 时，有

$$\sin{x} = x - \dfrac{1}{3!}x^3 + \dfrac{1}{5!}x^5 - \cdots + (-1)^{n-1}\dfrac{1}{(2n - 1)!}x^{2n - 1} + R_{2n}(x)\\ R_{2n} = \frac{\sin(\theta x + \frac{\pi}{2}(2n + 1))}{(2n + 1)!}x^{2n + 1} \quad (0 < \theta < 1)$$

对每个固定的 $x \in (-\infty, +\infty)$，有

$$\lim_{n \to \infty} R_{2n}(x) = \lim_{n \to \infty} \frac{\sin(\theta x + \frac{\pi}{2}(2n + 1))}{(2n + 1)!}x^{2n + 1} = 0$$

（3）$\cos{x} = 1 - \dfrac{1}{2!}x^2 + \dfrac{1}{4!}x^4 - \cdots + (-1)^n\dfrac{1}{(2n)!}x^{2n} + \cdots$

间接法：

$$\begin{aligned} \cos x &= (\sin x)' = \left[ \sum_{n = 1}^\infty(-1)^{n - 1}\frac{x^{2n - 1}}{(2n - 1)!} \right]'\\ &= \sum_{n = 1}^\infty\left[ \frac{(-1)^{n - 1}}{(2n - 1)!}x^{2n - 1} \right]'\\ &= \sum_{n = 1}^\infty\frac{(-1)^n}{(2n)!}x^{2n} \end{aligned}$$

（4）$\ln(1 + x) = x - \dfrac{1}{2}x^2 + \dfrac{1}{3}x^3 - \cdots + (-1)^n\dfrac{1}{n + 1}x^{n + 1} + \cdots, \quad (-1 < x \leq 1)$

间接法：

$$\begin{aligned} \ln(1 + x) &= \int_0^x \sum_{n = 0}^\infty (-1)^n t^n \mathrm{d}t = \sum_{n = 0}^\infty \int_0^x (-1)^n t^n \mathrm{d}t\\ &= \sum_{n = 0}^\infty (-1)^n\frac{x^{n + 1}}{n + 1} \end{aligned}$$

（5）$\arctan{x} = \sum\limits_{n = 0}^\infty (-1)^n\dfrac{x^{2n + 1}}{2n + 1}, \quad (|x| \leq 1)$

间接法：

$$\begin{aligned} \arctan x &= \int_0^x \sum_{n = 0}^\infty (-1)^n t^{2n} \mathrm{d}t = \sum_{n = 0}^\infty \int_0^x (-1)^n t^{2n} \mathrm{d}t\\ &= \sum_{n = 0}^\infty (-1)^n \frac{x^{2n + 1}}{2n + 1} \end{aligned}$$

（6）$(1 + x)^\alpha = 1 + \alpha x + \dfrac{\alpha(\alpha - 1)}{2!}x^2 + \cdots + \dfrac{\alpha(\alpha - 1) \cdots (\alpha - n + 1)}{n!}x^n + \cdots, \quad (|x| < 1)$

上式右端级数称为二项式级数，当 $\alpha$ 是正整数时，就是通常的二项式公式。

幂级数的应用

1. 利用幂函数展开式进行近似计算：

例：计算 $\sqrt[9]{522}$ 的近似值，要求精确到 $10^{-4}$.

解：因为

$$\sqrt[9]{522} = 2\left( 1 + \frac{10}{2^9} \right)^{\frac{1}{9}}$$

所以在二项式级数中取 $\alpha = \dfrac{1}{9}, x = \dfrac{10}{2^9}$，则有

$$2\left( 1 + \frac{10}{2^9} \right)^{\frac{1}{9}} = 2\left[ 1 + \frac{1}{9} \cdot \frac{10}{2^9} + \frac{\frac{1}{9}\left( \frac{1}{9} - 1 \right)}{2!} \cdot \frac{10^2}{2^{18}} + \cdots \right]$$

由于

$$\frac{\frac{1}{9} \cdot \frac{8}{9}}{2!} \cdot \frac{10^2}{2^{18}} = 0.000019 < 10^{-4}$$

而上述级数为交错级数 $\sum (-1)^{n - 1}u_n$，故有估计式

$$|S - S_n| \leq u_{n + 1}$$

由此可知，取级数的前两项和作为近似值即可达到要求，所以

$$\sqrt[9]{522} \approx 2(1 + 0.00217) \approx 2.0043$$

2. 欧拉公式的形式推导： 在 $\mathrm{e}^x$ 的展开式中将 $x$ 换成 $\mathrm{i}x$，可得

$$\begin{aligned} \mathrm{e}^{\mathrm{i}x} &= 1 + \mathrm{i}x + \frac{(\mathrm{i}x)^2}{2!} + \frac{(\mathrm{i}x)^3}{3!} + \frac{(\mathrm{i}x)^4}{4!} + \frac{(\mathrm{i}x)^5}{5!} + \cdots\\ &= 1 + \mathrm{i}x - \frac{x^2}{2!} - \frac{\mathrm{i}x^3}{3!} + \frac{x^4}{4!} + \frac{\mathrm{i}x^5}{5!} + \cdots\\ &= \left( 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \cdots \right) + \mathrm{i}\left( x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots \right)\\ &= \cos x + \mathrm{i}\sin x \end{aligned}$$

同理可得

$$\mathrm{e}^{-\mathrm{i}x} = \cos x - \mathrm{i}\sin x$$

将此二式相加，可得

$$\cos x = \frac{1}{2}\left( \mathrm{e}^{\mathrm{i}x} + \mathrm{e}^{-\mathrm{i}x} \right)$$

同理可得

$$\sin x = \frac{1}{2\mathrm{i}}\left( \mathrm{e}^{\mathrm{i}x} - \mathrm{e}^{-\mathrm{i}x} \right)$$

3. 求解积分方程： 许多积分方程的解都可以表示成级数的形式，对于形如

$$y(x) = \lambda \int_a^x k(x, t)y(t)\mathrm{d}t + f(x)$$

的积分方程，其中 $\lambda$ 为已知参数，$f(x)$ 为 $[a, b]$ 上的连续函数，$k(x, t)$ 为 $[a, b]^2$ 上的连续函数，$y(x)$ 为未知函数。可以证明其解为

$$y^*(x) = f(x) + \sum_{n = 1}^\infty \lambda^n\varPhi_n(x)$$

其中 $\displaystyle\varPhi_0(x) = f(x), \varPhi_n(x) = \int_a^x k(x, t)\varPhi_{n - 1}(t)\mathrm{d}t, n = 1, 2, \cdots$.

傅里叶级数

三角函数系的正交性与三角级数

三角函数系中每个函数的周期都是 $2\pi$，我们通常选取 $[-\pi, \pi]$，并在该区间上讨论三角函数。对任意正整数 $m, n\ (m \neq n)$，有

$$\begin{aligned} \int_{-\pi}^\pi \cos{n}x\mathrm{d}x &= \int_{-\pi}^\pi \sin{n}x\mathrm{d}x = 0\\ \int_{-\pi}^\pi \cos{m}x \cdot \cos{n}x\mathrm{d}x &= \frac{1}{2}\int_{-\pi}^{\pi} [\cos(m + n)x + \cos(m - n)x]\mathrm{d}x\\ &= 0\\ \int_{-\pi}^\pi \sin{m}x \cdot \sin{n}x\mathrm{d}x &= -\frac{1}{2}\int_{-\pi}^{\pi} [\cos(m + n)x - \cos(m - n)x]\mathrm{d}x\\ &= 0\\ \int_{-\pi}^\pi \sin{m}x \cdot \cos{n}x\mathrm{d}x &= 0\\ \end{aligned}$$

由此可见，三较函数系中任意两个相异函数的乘积在区间 $[-\pi, \pi]$ 上的积分为零，这个性质称为三角函数系在区间 $[-\pi, \pi]$ 上的正交性。

三角函数的积分等式：

$$\begin{aligned} \int_{-\pi}^\pi \mathrm{d}x &= 2\pi\\ \int_{-\pi}^\pi \cos^2{nx}\mathrm{d}x &= \int_{-\pi}^\pi \frac{1 + \cos{2nx}}{2}\mathrm{d}x = \pi\\ \int_{-\pi}^\pi \sin^2{nx}\mathrm{d}x &= \int_{-\pi}^\pi \frac{1 - \cos{2nx}}{2}\mathrm{d}x = \pi \end{aligned}$$

三角级数： 形如

$$\frac{a_0}{2} + \sum_{n = 1}^\infty(a_n \cos{nx} + b_n \sin{nx})$$

的函数项级数称为三角级数。

以 2π 为周期的函数展开成傅里叶级数

定理： 假设以 $2\pi$ 为周期的可积函数 $f(x)$ 能展开成三角级数，且

$$f(x) = \frac{a_0}{2} + \sum_{n = 1}^\infty(a_n \cos{nx} + b_n \sin{nx})$$

的右端级数可以逐项积分，则三角级数中的系数和 $f(x)$ 必然满足如下关系：

$$\begin{cases} \displaystyle a_k = \frac{1}{\pi}\int_{-\pi}^\pi f(x)\cos{kx}\mathrm{d}x, & k = 0, 1, 2, \cdots\\ \displaystyle b_k = \frac{1}{\pi}\int_{-\pi}^\pi f(x)\sin{kx}\mathrm{d}x, & k = 1, 2, \cdots \end{cases}$$

按上式计算出的系数 $a_k, b_k$ 称为函数 $f(x)$ 的傅里叶系数，以该系数作成的三角级数称为 $f(x)$ 的傅里叶级数，记作：

$$f(x) \sim \frac{a_0}{2} + \sum_{n = 1}^\infty(a_n \cos{nx} + b_n \sin{nx})$$

证明：对原式两端逐项积分，可得

$$\int_{-\pi}^\pi f(x)\mathrm{d}x = \frac{a_0}{2}\int_{-\pi}^\pi \mathrm{d}x + \sum_{n = 1}^\infty \left( a_n\int_{-\pi}^\pi\cos{nx}\mathrm{d}x + b_n\int_{-\pi}^\pi\sin{nx}\mathrm{d}x \right) = a_0\pi$$

从而

$$a_0 =\frac{1}{\pi}\int_{-\pi}^\pi f(x)\mathrm{d}x$$

若在两端同时乘上 $\cos{kx}$，再进行逐项积分，由三角函数系的正交性可得

$$\begin{aligned} & \int_{-\pi}^\pi f(x)\cos{kx}\mathrm{d}x\\ = & \frac{a_0}{2} \int_{-\pi}^\pi \cos{kx}\mathrm{d}x + \sum_{n = 1}^\infty\left( a_n\int_{-\pi}^\pi \cos{kx} \cdot \cos{nx}\mathrm{d}x + b_n\int_{-\pi}^\pi \cos{kx} \cdot \sin{nx}\mathrm{d}x \right)\\ = & a_k \int_{-\pi}^\pi \cos^2{kx}\mathrm{d}x = a_k \pi \end{aligned}$$

从而有

$$a_k = \frac{1}{\pi}\int_{-\pi}^\pi f(x)\cos{kx}\mathrm{d}x$$

同理可得

$$b_k = \frac{1}{\pi}\int_{-\pi}^\pi f(x)\sin{kx}\mathrm{d}x$$

例：设 $f(x) = \mathrm{e}^x, \ x \in (-\pi, \pi)$，求其傅里叶级数。

解：

$$a_0 = \frac{1}{\pi}\int_{-\pi}^\pi \mathrm{e}^x\mathrm{d}x = \frac{1}{\pi}(\mathrm{e}^\pi - \mathrm{e}^{-\pi})$$

$$\begin{aligned} a_n &= \frac{1}{\pi}\int_{-\pi}^\pi \mathrm{e}^x\cos{nx}\mathrm{d}x = \frac{1}{\pi}\int_{-\pi}^\pi \cos{nx}\mathrm{de}^x\\ &= \frac{1}{\pi}\left( \cos{nx}\mathrm{e}^x \bigg|_{-\pi}^\pi + \int_{-\pi}^\pi n\mathrm{e}^x\sin{nx}\mathrm{d}x \right)\\ &= \frac{1}{\pi}\left( \cos{n \pi \mathrm{e}^\pi} - \cos{n \pi \mathrm{e}^{-\pi}} + n\int_{-\pi}^\pi \sin{nx}\mathrm{de}^x \right)\\ &= \frac{1}{\pi}(-1)^n(\mathrm{e}^\pi - \mathrm{e}^{-\pi}) - \frac{n^2}{\pi}\int_{-\pi}^\pi \mathrm{e}^x \cos{nx}\mathrm{d}x\\ &= \frac{(-1)^n}{(n^2 + 1)\pi}(\mathrm{e}^\pi - \mathrm{e}^{-\pi}) \end{aligned}$$

$$\begin{aligned} b_n &= \frac{1}{\pi} \int_{-\pi}^\pi \mathrm{e}^x \sin{nx} \mathrm{d}x = \frac{1}{\pi} \int_{-\pi}^\pi \sin{nx} \mathrm{de}^x\\ &= \frac{1}{\pi} \left( \mathrm{e}^x \sin{nx} \bigg|_{-\pi}^\pi - \int_{-\pi}^\pi \mathrm{e}^x n\cos{nx} \mathrm{d}x \right) = -\frac{n}{\pi} \int_{-\pi}^\pi \cos{nx} \mathrm{de}^x\\ &= -\frac{n}{\pi} \left( \mathrm{e}^x \cos{nx}\bigg|_{-\pi}^\pi + \int_{-\pi}^\pi n\mathrm{e}^x \sin{nx} \mathrm{d}x \right)\\ &= \frac{(-1)^{n + 1}n}{(n^2 + 1)\pi}(\mathrm{e}^\pi - \mathrm{e}^{-\pi}) \end{aligned}$$

综上所述，所求傅里叶级数为

$$\mathrm{e}^x \sim \frac{\mathrm{e}^\pi - \mathrm{e}^{-\pi}}{\pi} \left\{ \frac{1}{2} + \sum_{n = 1}^\infty \left[ \frac{(-1)^n}{n^2 + 1} \cos{nx} + \frac{(-1)^{n + 1}n}{(n^2 + 1)\pi} \sin{nx} \right] \right\}, \quad -\pi < x < \pi$$

狄利克雷（Dirichlet）收敛定理： 若以 $2\pi$ 为周期的函数 $f(x)$ 在 $[-\pi, \pi]$ 上满足狄利克雷条件：

1. 连续或只有有限个第一类间断点；
2. 至多只有有限个极值点。

则 $f(x)$ 的傅里叶级数收敛，并且

• 当 $x$ 是 $f(x)$ 的连续点时，级数收敛于 $f(x)$；
• 当 $x$ 是 $f(x)$ 的间断点时，级数收敛于 $\dfrac{1}{2}[f(x - 0) + f(x + 0)]$；
• 当 $x = \pm\pi$ 时，级数收敛于 $\dfrac{1}{2}[f(-\pi + 0) + f(\pi - 0)]$.

傅里叶级数中的各项都以 $2\pi$ 为周期，因此若它在 $[-\pi, \pi]$ 上收敛，则它在任意 $x$ 处都收敛。
在具体讨论函数的傅里叶级数时，常只给出函数 $f(x)$ 在 $(-\pi, \pi]$（或 $[-\pi, \pi)$）上的解析表达式，但应理解为它是定义在整个数轴上以 $2\pi$ 为周期的函数，可在给出区间以外部分按对应关系作周期延拓。

例：设

$$f(x) = \begin{cases} -1, & -\pi < x \leq 0 \\ 1 + x^2, & 0 < x < \pi \\ \end{cases}$$

则 $f(x)$ 的以 $2\pi$ 为周期的傅里叶级数在 $x = \pi$ 处收敛于 $\dfrac{\pi^2}{2}$.

函数展开成正弦级数或余弦级数

奇、偶函数的展开：

当 $f(x)$ 为奇函数时，$f(x)\cos{nx}$ 是奇函数，$f(x)\sin{nx}$ 是偶函数，于是 $f(x)$ 的傅里叶系数为

$$\begin{aligned} a_n &= \frac{1}{\pi}\int_{-\pi}^\pi f(x)\cos{nx}\mathrm{d}x = 0, \quad n = 0, 1, 2, \cdots\\ b_n &= \frac{1}{\pi}\int_{-\pi}^\pi f(x)\sin{nx}\mathrm{d}x = \frac{2}{\pi}\int_0^\pi f(x)\sin{nx}\mathrm{d}x, \quad n = 1, 2, \cdots \end{aligned}$$

此时奇函数 $f(x)$ 的傅里叶级数只含正弦项，称为正弦级数，即

$$f(x) \sim \sum_{n = 1}^\infty b_n \sin{nx}$$

同样地，当 $f(x)$ 为偶函数时，$f(x)\cos{nx}$ 是偶函数，$f(x)\sin{nx}$ 是奇函数，于是 $f(x)$ 的傅里叶级数为

$$\begin{aligned} a_n &= \frac{2}{\pi}\int_0^\pi f(x)\cos{nx}\mathrm{d}x, \quad n = 0, 1, 2, \cdots\\ b_n &= 0, \quad n = 1, 2, \cdots \end{aligned}$$

此时偶函数 $f(x)$ 的傅里叶级数只含常数项和余弦项，称为余弦级数，即

$$f(x) \sim \frac{a_0}{2} + \sum_{n = 1}^\infty a_n \cos{nx}$$

函数展开成正弦级数或余弦级数：

设函数定义在闭区间 $[0, \pi]$ 或 $[-\pi, 0]$ 上，并且满足收敛定理的条件，若想将其展开成正弦级数或余弦级数，则需要在开区间 $(-\pi, 0)$ 或 $(0, \pi)$ 内补充定义，得到 $(-\pi, \pi)$ 上的奇函数（偶函数），按这种方法拓广函数定义域的过程称为奇延拓（偶延拓）。

将延拓后的函数展开成傅里叶级数，则这个级数必定是正弦级数或余弦级数，这样便可以得到 $f(x)$ 的正弦级数或余弦级数展开式。

例：将函数 $f(x) = x^2\ (0 \leq x \leq \pi)$ 分别展开成正弦级数和余弦级数。

解：先求正弦级数，对 $f(x)$ 进行奇延拓，如下图所示：

则根据奇函数的展开公式，可得

$$\begin{aligned} a_n &= 0, \quad n = 0, 1, 2, \cdots\\ b_n &= \frac{2}{\pi} \int_0^\pi f(x) \sin{nx} \mathrm{d}x = \frac{2}{\pi} \int_0^\pi x^2 \sin{nx} \mathrm{d}x\\ &= \frac{2}{\pi} \left[ -\frac{1}{n} x^2 \cos{nx}\bigg|_0^\pi + \frac{2}{\pi} \int_0^\pi x\cos{nx} \mathrm{d}x \right]\\ &= \frac{2}{\pi} \left[ \frac{(-1)^{n + 1}\pi^2}{n} + \frac{2}{n^2} x\sin{nx}\bigg|_0^\pi - \frac{2}{n^2} \int_0^\pi \sin{nx}\mathrm{d}x \right]\\ &= \frac{2}{\pi} \left[ \frac{(-1)^{n + 1}\pi^2}{n} + \frac{2}{n^3} \cos{nx}\bigg|_0^\pi \right]\\ &= \frac{2}{\pi} \left[ \frac{(-1)^{n + 1}\pi^2}{n} + \frac{2}{n^3}((-1)^n - 1) \right], \quad n = 1, 2, \cdots \end{aligned}$$

所以

$$f(x) \sim \frac{2}{\pi} \sum_{n = 1}^\infty \left[ (-1)^n \left( \frac{2}{n^3} - \frac{\pi^2}{n} \right) - \frac{2}{n^3} \right] \sin{nx}, \quad 0 \leq x < \pi$$

由狄利克雷收敛定理可得，当 $x = \pi$ 时，级数收敛于 $0$.

再求余弦级数，对 $f(x)$ 进行偶延拓，如下图所示：

则根据偶函数的展开公式，可得

$$\begin{aligned} b_n &= 0, \quad n = 1, 2, 3, \cdots\\ a_0 &= \frac{2}{\pi} \int_0^\pi x^2 \mathrm{d}x = \frac{2}{3} \pi^2\\ a_n &= \frac{2}{\pi} \int_0^\pi x^2 \cos{nx}\mathrm{d}x = \frac{2}{n\pi} \int_0^\pi x^2 \mathrm{d}\sin{nx}\\ &= \frac{2}{n\pi} \left( x^2 \sin{nx}\bigg|_0^\pi - \int_0^\pi 2x\sin{nx} \mathrm{d}x \right)\\ &= \frac{4}{n^2 \pi} \int_0^\pi x \mathrm{d}\cos{nx}\\ &= \frac{4}{n^2 \pi} \left( x\cos{nx}\bigg|_0^\pi - \int_0^\pi \cos{nx} \mathrm{d}x \right)\\ &= \frac{4}{n^2} (-1)^n, \quad n = 1, 2, \cdots \end{aligned}$$

所以

$$f(x) \sim \frac{\pi^2}{3} + 4\sum_{n = 1}^\infty \frac{(-1)^n}{n^2} \cos{nx}, \quad 0 \leq x < \pi$$

由狄利克雷收敛定理可得，当 $x = \pi$ 时，级数收敛于 $f(\pi)$，故

$$f(x) \sim \frac{\pi^2}{3} + 4\sum_{n = 1}^\infty \frac{(-1)^n}{n^2} \cos{nx}, \quad 0 \leq x \leq \pi$$

以 2l 为周期的函数展开成傅里叶级数

设 $f(x)$ 是以 $2l$ 为周期的函数，则通过变量代换 $x = \dfrac{lt}{\pi}$ 可以将 $f(x)$ 转换为以 $2\pi$ 为周期的函数 $F(t)$. 显然对任意 $t$，有

$$F(t + 2\pi) = f\left[ \frac{l(t + 2\pi)}{\pi} \right] = f\left( \frac{lt}{\pi} + 2l \right) = f\left( \frac{lt}{\pi} \right)$$

若 $f(x)$ 在 $[-l, l]$ 上可积，则 $F(t)$ 在 $[-\pi, \pi]$ 上也可积，此时 $F(t)$ 的傅里叶级数为

$$F(t) \sim \frac{a_0}{2} + \sum_{n = 1}^\infty (a_n \cos{nt} + b_n \sin{nt})$$

其中

$$\begin{cases} \displaystyle a_n = \frac{1}{l} \int_{-\pi}^\pi F(t) \cos{nt} \mathrm{d}t, & n = 0, 1, 2, \cdots \\ \displaystyle b_n = \frac{1}{l} \int_{-l}^l F(t) \sin{nt} \mathrm{d}t, & n = 1, 2, \cdots \\ \end{cases}$$

作代换 $t = \dfrac{\pi x}{l}$，则有

$$f(x) \sim \frac{a_0}{2} + \sum_{n = 1}^\infty \left( a_n \cos\frac{n \pi x}{l} + b_n \sin\frac{n \pi x}{l} \right)\\ \begin{cases} \displaystyle a_n = \frac{1}{\pi} \int_{-l}^l f(x) \cos\frac{n \pi x}{l} \mathrm{d}x, & n = 0, 1, 2, \cdots \\ \displaystyle b_n = \frac{1}{\pi} \int_{-\pi}^\pi f(x) \sin\frac{n \pi x}{l} \mathrm{d}x, & n = 1, 2, \cdots \\ \end{cases}$$

称为以 $\bm{2l}$ 为周期的函数 $f(x)$ 的傅里叶系数公式。

如果要对以 $2l$ 为周期的函数应用狄利克雷收敛定理，只需要将狄利克雷条件中的 $[-\pi, \pi]$ 换成 $[-l, l]$ 即可。

将以 $2l$ 为周期的奇函数 $f(x)$ 展开成正弦级数：

$$\begin{aligned} b_n &= \frac{1}{l}\int_{-l}^l f(x)\sin\frac{n \pi x}{l}\mathrm{d}x\\ &= \frac{2}{l}\int_0^l f(x)\sin\frac{n \pi x}{l}\mathrm{d}x, \quad n = 1, 2, \cdots \end{aligned}\\ f(x) \sim \sum_{n = 1}^\infty b_n \sin\frac{n \pi x}{l}$$

将以 $2l$ 为周期的偶函数 $f(x)$ 展开成余弦级数：

$$\begin{aligned} a_n &= \frac{1}{l}\int_{-l}^l f(x)\cos\frac{n \pi x}{l}\mathrm{d}x\\ &= \frac{2}{l}\int_0^l f(x)\cos\frac{n \pi x}{l}\mathrm{d}x, \quad n = 0, 1, 2, \cdots \end{aligned}\\ f(x) \sim \frac{a_0}{2} + \sum_{n = 1}^\infty a_n \cos\frac{n \pi x}{l}$$

若想要将以 $2l$ 为周期的函数展开成正弦级数或余弦级数的形式，也需要通过奇延拓或偶延拓的方式补充定义，再求延拓后函数的傅里叶级数。

傅里叶级数的复数形式

由欧拉公式

$$\cos\frac{n \pi x}{l} = \frac{1}{2}(\mathrm{e}^{\mathrm{i}\frac{n \pi x}{l}} + \mathrm{e}^{-\mathrm{i}\frac{n \pi x}{l}}), \quad \sin\frac{n \pi x}{l} = \frac{1}{2\mathrm{i}}(\mathrm{e}^{\mathrm{i}\frac{n \pi x}{l}} - \mathrm{e}^{-\mathrm{i}\frac{n \pi x}{l}})$$

可得周期为 $2l$ 的函数 $f(x)$ 的傅里叶级数可以写成

$$\begin{aligned} f(x) &\sim \frac{a_0}{2} + \sum_{n = 1}^\infty \left[ \frac{a_n}{2}(\mathrm{e}^{\mathrm{i}\frac{n \pi x}{l}} + \mathrm{e}^{-\mathrm{i}\frac{n \pi x}{l}}) + \frac{b_n}{2\mathrm{i}}(\mathrm{e}^{\mathrm{i}\frac{n \pi x}{l}} - \mathrm{e}^{-\mathrm{i}\frac{n \pi x}{l}}) \right]\\ &= \frac{a_0}{2} + \sum_{n = 1}^\infty \left( \frac{a_n - \mathrm{i}b_n}{2}\mathrm{e}^{\mathrm{i}\frac{n \pi x}{l}} + \frac{a_n + \mathrm{i}b_n}{2}\mathrm{e}^{-\mathrm{i}\frac{n \pi x}{l}} \right) \end{aligned}$$

若记

$$w = \frac{\pi}{l}, c_0 = \frac{a_0}{2}, c_n = \frac{a_n - \mathrm{i}b_n}{2}, c_{-n} = \frac{a_n + \mathrm{i}b_n}{2}, \ n = 1, 2, \cdots$$

则 $f(x)$ 的傅里叶级数的复数形式为

$$f(x) = c_0 + \sum_{n = 1}^\infty c_n \mathrm{e}^{\mathrm{i} n \omega x} + \sum_{n = 1}^\infty c_{-n} \mathrm{e}^{-\mathrm{i} n \omega x} = \sum_{n = -\infty}^\infty c_n \mathrm{e}^{\mathrm{i} n \omega x}$$

傅里叶系数的复数形式为

$$c_n = \frac{1}{2l} \int_{-l}^l f(x) \mathrm{e}^{-\mathrm{i} n \omega x} \mathrm{d}x \quad n = 0, \pm 1, \pm 2, \cdots$$

以 $2\pi$ 为周期的函数 $f(x)$ 的傅里叶级数可以写成

$$f(x) = \sum_{n = -\infty}^\infty c_n \mathrm{e}^{\mathrm{i} nx}$$

傅里叶系数的复数形式为

$$c_n = \frac{1}{2\pi} \int_{-\pi}^\pi f(x) \mathrm{e}^{-\mathrm{i} nx} \mathrm{d}x \quad n = 0, \pm 1, \pm 2, \cdots$$

常微分方程

常微分方程的基本概念

含有自变量、未知函数及某些导数（或微分）的方程称为微分方程，未知函数是一元函数的微分方程称为常微分方程，未知函数是多元函数的微分方程称为偏微分方程。一个微分方程中出现的未知函数导数的最阶数称为此微分方程的阶，一般地，$n$ 阶常微分方程可以表示为如下隐方程和显方程：

$$F(x, y, y', \cdots, y^{(n)}) = 0\\ y^{(n)} = f(x, y, y', \cdots, y^{(n - 1)})$$

如果一个常微分方程关于未知函数及其导数都是线性的，则称之为线性微分方程，否则称为非线性微分方程。

常微分方程的解： 设函数 $y = y(x)$ 在区间 $I$ 上有定义，且存在 $n$ 阶导数，如果将 $y = y(x)$ 及其各阶导数代入常微分方程后能使其成为区间 $I$ 上的恒等式，即

$$F[x, y(x), y'(x), \cdots, y^{(n)}(x)] \equiv 0$$

或

$$y^{(n)}(x) \equiv f[x, y(x), y'(x), \cdots, y^{(n - 1)}(x)]$$

则称函数 $y = y(x)$ 为常微分方程在区间 $I$ 上的一个解。微分方程解的图形称为积分曲线。

如果 $n$ 阶常微分方程的解 $y = \varphi(x, C_1, C_2, \cdots, C_n)$ 中含有 $n$ 个互相独立的任意常数 $C_1, C_2, \cdots, C_n$，则称其为方程的通解；如果由含 $n$ 个相互独立的任意常数 $C_1, C_2, \cdots, C_n$ 的方程 $\varPhi(x, y, C_1, C_2, \cdots, C_n) = 0$ 确定的函数 $y = y(x, C_1, C_2, \cdots, C_n)$ 是 $n$ 阶常微分方程的解，则称此函数为方程的隐式通解。通解中的任意常数确定后，所得到的确定的解称为微分方程的特解。

为了确定通解中的任意常数，需要给出微分方程所满足的定解条件，常见的定解条件是初始条件。一般地，$n$ 阶微分方程的初始条件是

$$y(x_0) = y_0, y'(x_0) = y_1, \cdots, y^{(n - 1)}(x_0) = y_{n - 1}$$

其中 $x_0, y_0, y_1, \cdots, y_{n - 1}$ 都是给定的值。

求微分满足初始条件的特解的问题称为初值问题或柯西问题。

可分离变量的微分方程

形如

$$\frac{\mathrm{d}y}{\mathrm{d}x} = f(x)g(y)$$

的方程称为可分离变量方程，其中 $f(x), g(y)$ 分别是 $x, y$ 的连续函数。

求解过程： 当 $g(y) \neq 0$ 时，可以将方程改写为变量分离的形式

$$\frac{\mathrm{d}y}{g(y)} = f(x) \mathrm{d}x$$

两端分别对 $y$ 和 $x$ 积分可得

$$\int \frac{\mathrm{d}y}{g(y)} = \int f(x) \mathrm{d}x$$

该式即为方程的隐式通解。

若存在 $y_0$ 使得 $g(y_0) = 0$，易知 $y = y_0$ 为方程的一个解，于是方程除了有上述通解以外，还可能存在一些常数解。

例：求常微分方程 $\dfrac{\mathrm{d}y}{\mathrm{d}x} = \dfrac{y}{x}$ 的通解。

解：当 $y \neq 0$ 时，分离变量可得

$$\frac{\mathrm{d}y}{y} = \frac{\mathrm{d}x}{x}$$

两端积分得

$$\ln|y| = \ln|x| + C_1$$

从而 $|y| = \mathrm{e}^{C_1}|x|$，令 $C = \pm \mathrm{e}^{C_1} \neq 0$，则 $y = Cx$.
注意到 $y = 0$ 也是方程的解。令 $C$ 为任意常数，则可得所给方程得通解为

$$y = Cx$$

可分离变量方程也可以写成关于 $x$ 和 $y$ 的对称形式：

$$M_1(x)M_2(y) \mathrm{d}x + N_1(x)N_2(y) \mathrm{d}y = 0$$

当 $M_2(y)N_1(x) \neq 0$ 时，两端同时除以 $M_2(y)N_1(x)$，可得

$$\frac{M_1(x)}{N_1(x)} \mathrm{d}x + \frac{N_2(y)}{M_2(y)} \mathrm{d}y = 0$$

等式两端积分，可得方程的通解为

$$\int \frac{M_1(x)}{N_1(x)} \mathrm{d}x + \int \frac{N_2(y)}{M_2(y)} \mathrm{d}y = C$$

其中 $C$ 为任意常数。

若存在 $x_0, y_0$ 使得 $N_1(x_0) = 0$ 或 $M_2(y_0) = 0$，则易知 $x = x_0$ 或 $y = y_0$ 也是方程的解。

齐次微分方程

形如

$$\frac{\mathrm{d}y}{\mathrm{d}x} = \varphi \left( \frac{y}{x} \right)$$

的方程称为齐次微分方程。

求解过程： 若 $\varphi$ 为连续函数，可令 $u = \dfrac{y}{x}$，即 $y = xu$，从而 $\dfrac{\mathrm{d}y}{\mathrm{d}x} = u + x\dfrac{\mathrm{d}u}{\mathrm{d}x}$，代入原方程中得 $u + x\dfrac{\mathrm{d}u}{\mathrm{d}x} = \varphi(u)$，即

$$\frac{\mathrm{d}u}{\mathrm{d}x} = \frac{\varphi(u) - u}{x}$$

当 $\varphi(u) - u \neq 0$ 时，分离变量后积分得

$$\int \frac{\mathrm{d}u}{\varphi(u) - u} = \int \frac{\mathrm{d}x}{x}$$

记 $\varPhi(u)$ 为 $\dfrac{\mathrm{d}u}{\varphi(u) - u}$ 的一个原函数，则可得

$$\varPhi(u) = \ln|x| + C$$

再将 $u = \dfrac{y}{x}$ 代入，便可得到齐次微分方程的通解

$$\varPhi \left( \frac{y}{x} \right) = \ln|x| + C$$

若存在函数 $u_0$，使得 $\varphi(u_0) - u_0 = 0$，则 $u = u_0$ 即 $y = u_0 x$ 也是齐次微分方程的解。

例：求解常微分方程

$$\frac{\mathrm{d}y}{\mathrm{d}x} = 2\sqrt{\frac{y}{x}} + \frac{y}{x}$$

解：令 $u = \dfrac{y}{x}$，代入方程得

$$u + x\frac{\mathrm{d}u}{\mathrm{d}x} = 2\sqrt{u} + u$$

即

$$x\frac{\mathrm{d}u}{\mathrm{d}x} = 2\sqrt{u}$$

当 $u \neq 0$ 时，分离变量后积分得

$$u = (\ln|x| + C)^2$$

将 $u = \dfrac{y}{x}$ 代入上式可得通解

$$y = x(\ln|x| + C)^2$$

当 $u = 0$ 时，得到 $y = 0\ (x \neq 0)$ 也是该方程的解。

形如

$$\frac{\mathrm{d}y}{\mathrm{d}x} = f\left( \frac{ax + by + c}{a_1 x + b_1 y + c_1} \right)$$

的方程称为准齐次方程，其中 $a, b, c, a_1, b_1, c_1$ 都是常数。

当 $c = c_1 = 0$ 时，该方程即为齐次方程；当 $c$ 和 $c_1$ 中至少有一个不为零时，可经过适当的变换将该方程化为齐次方程。

求解过程 1： 当 $\Delta = \begin{vmatrix} a & b \\ a_1 & b_1 \end{vmatrix} \neq 0$ 时，引入新的变量

$$x = X + \alpha, \quad y = Y + \beta$$

其中 $\alpha, \beta$ 为待定常数。

代入原方程可得

$$\frac{\mathrm{d}Y}{\mathrm{d}X} = f\left( \frac{aX + bY + a\alpha + b\beta + c}{a_1 X + b_1 Y + a_1 \alpha + b_1 \beta + c_1} \right)$$

为使该方程是齐次的，应选 $\alpha, \beta$ 满足

$$\begin{cases} a\alpha + b\beta + c = 0\\ a_1\alpha + b_1\beta + c_1 = 0 \end{cases}$$

因为 $\Delta \neq 0$，所以这样的 $\alpha, \beta$ 存在且唯一，于是有

$$\frac{\mathrm{d}Y}{\mathrm{d}X} = f\left( \frac{aX + bY}{a_1 X + b_1 Y} \right)$$

如果函数为 $Y = Y(X)$ 为上述方程的解，则函数

$$y = Y(x - \alpha) + \beta$$

就是原方程的解。

例：求解方程 $\dfrac{\mathrm{d}y}{\mathrm{d}x} = \dfrac{-x + y - 2}{x + y + 4}$.

解：令 $x = X + \alpha, y = Y + \beta$，代入方程中得

$$\frac{\mathrm{d}Y}{\mathrm{d}X} = \frac{-X + Y - \alpha + \beta - 2}{X + Y + \alpha + \beta + 4}$$

由

$$\begin{cases} -\alpha + \beta - 2 = 0\\ \alpha + \beta + 4 = 0 \end{cases}$$

解得 $\alpha = -3, \beta = -1$.

对方程 $\dfrac{\mathrm{d}Y}{\mathrm{d}X} = \dfrac{-X + Y}{X + Y}$，将分子、分母同除 $X$ 得

$$\frac{\mathrm{d}Y}{\mathrm{d}X} = \frac{-1 + \dfrac{Y}{X}}{1 + \dfrac{Y}{X}}$$

令 $u = \dfrac{Y}{X}$，得 $u + X\dfrac{\mathrm{d}u}{\mathrm{d}X} = \dfrac{-1 + u}{1 + u}$，整理得

$$\begin{aligned} X\frac{\mathrm{d}u}{\mathrm{d}X} &= -\frac{1 + u^2}{1 + u}\\ \frac{(1 + u)\mathrm{d}u}{1 + u^2} &= -\frac{\mathrm{d}X}{X} \end{aligned}$$

两端积分有

$$\begin{aligned} \arctan{u} + \frac{1}{2}\ln(1 + u^2) &= -\ln|X| + C_1\\ \frac{1}{2}\left[ \ln\left(1 + \frac{Y^2}{X^2}\right) + 2\ln|X| \right] &= C_1 - \arctan{u} \end{aligned}$$

即

$$\sqrt{X^2 + Y^2} = C\mathrm{e}^{-\arctan{\frac{Y}{X}}}$$

其中 $C = \mathrm{e}^{C_1}$ 为任意正实数。将 $x = X - 3, y = Y - 1$ 代入上式，即可得到原方程的隐式通解

$$\sqrt{(x + 3)^2 + (y + 1)^2} = C\mathrm{e}^{-\arctan{\frac{y + 1}{x + 3}}}$$

求解过程 2： 当 $\Delta = 0$ 时，亦即 $\dfrac{a_1}{a} = \dfrac{b_1}{b} = \lambda$，此时原方程可表示为

$$\frac{\mathrm{d}y}{\mathrm{d}x} = f\left( \frac{ax + by + c}{\lambda(ax + by) + c_1} \right)$$

令 $z = ax + by$，则有 $\dfrac{\mathrm{d}z}{\mathrm{d}x} = a + b\dfrac{\mathrm{d}y}{\mathrm{d}x}$，代入上述方程可得

$$\frac{\mathrm{d}z}{\mathrm{d}x} = a + bf\left( \frac{z + c}{\lambda z + c_1} \right)$$

若函数 $z = z(x)$ 是该方程的解，则函数

$$y = \frac{1}{b}[z(x) - ax]$$

就是原方程的解。

例：求解方程 $y' = \dfrac{x + 2y + 1}{2x + 4y - 1}$

解：令 $z = x + 2y$，则有

$$\frac{\mathrm{d}z}{\mathrm{d}x} = 1 + 2\frac{\mathrm{d}y}{\mathrm{d}x}$$

代入原方程可得

$$\begin{aligned} \frac{\mathrm{d}z}{\mathrm{d}x} &= 1 + \frac{2(z + 1)}{2z - 1}\\ \frac{\mathrm{d}z}{\mathrm{d}x} &= \frac{4z + 1}{2z - 1}\\ \frac{1}{2}\left( 1 - \frac{3}{4z + 1} \right)\mathrm{d}z &= \mathrm{d}x \end{aligned}$$

两端积分得

$$\begin{aligned} \frac{1}{2}\left( z - \frac{3}{4}\ln|4z + 1| \right) = x + C_1 \end{aligned}$$

整理得

$$4z - 3\ln|4z + 1| = 8x + C$$

将 $z = x + 2y$ 代入上式，可得原方程的通解为

$$8y - 4x - 3\ln|4x + 8y + 1| = C$$

一阶线性微分方程

形如

$$\frac{\mathrm{d}y}{\mathrm{d}x} = p(x)y + q(x)$$

的方程称为一阶线性微分方程。

当 $q(x) \equiv 0$ 时，原方程变为

$$\frac{\mathrm{d}y}{\mathrm{d}x} = p(x)y$$

称为一阶齐次线性微分方程，显然 $y = 0$ 是该方程的解。

当 $y \neq 0$ 时，分离变量得 $\dfrac{\mathrm{d}y}{y} = p(x)\mathrm{d}x$，再两端积分后可得

$$\ln|y| = \int p(x)\mathrm{d}x + C_1$$

从而 $y = C \mathrm{e}^{\int p(x) \mathrm{d}x}\ (C = \pm \mathrm{e}^{C_1} \neq 0)$，又因为 $y = 0$ 也是原方程的解，所以一阶齐次线性微分方程的通解为

$$y(x) = C \mathrm{e}^{\int p(x) \mathrm{d}x} \quad (C \ \text{为任意常数})$$

对于初值问题

$$\begin{cases} \dfrac{\mathrm{d}y}{\mathrm{d}x} = p(x)y, & a < x < b\\ y(x_0) = y_0, & x_0 \in (a, b) \end{cases}$$

可以证明其解为 $y(x) = y_0\mathrm{e}^{\int_{x_0}^x p(t) \mathrm{d}t}$.

当 $q(x) \not\!\equiv 0$ 时，原方程称为一阶非齐次线性微分方程，可采用常数变易法求其通解。

常数变易法：将对应的齐次微分方程的通解中的常数 $C$ 改为函数 $C(x)$，并通过适当选择 $C(x)$ 以得到非齐次微分方程的通解。

设 $y(x) = C(x) \mathrm{e}^{\int p(x) \mathrm{d}x}$ 是方程的解，则有恒等式

$$\left[ C(x)\mathrm{e}^{\int p(x) \mathrm{d}x} \right]' \equiv p(x)C(x)\mathrm{e}^{\int p(x) \mathrm{d}x} + q(x)$$

化简可得

$$C'(x) = q(x)\mathrm{e}^{-\int p(x) \mathrm{d}x}$$

两端积分得

$$C(x) = \int q(x)\mathrm{e}^{-\int p(x) \mathrm{d}x}$$

于是可得到一阶非齐次线性微分方程的通解为

$$\begin{aligned} y(x) &= \mathrm{e}^{\int p(x) \mathrm{d}x}\left( \int q(x)\mathrm{e}^{-\int p(x) \mathrm{d}x} \mathrm{d}x + C \right)\\ &= \mathrm{e}^{\int p(x) \mathrm{d}x}\int q(x)\mathrm{e}^{-\int p(x) \mathrm{d}x} \mathrm{d}x + C\mathrm{e}^{\int p(x) \mathrm{d}x} \end{aligned}$$

当 $C = 0$ 时，可以得到一个特解为

$$y^*(x) = \mathrm{e}^{\int p(x) \mathrm{d}x}\int q(x)\mathrm{e}^{-\int p(x) \mathrm{d}x} \mathrm{d}x$$

例：求解方程 $\dfrac{\mathrm{d}y}{\mathrm{d}x} = \dfrac{2}{x}y + \dfrac{1}{2}x$.

解：令 $p(x) = \dfrac{2}{x}, q(x) = \dfrac{1}{2}x$，则

$$\begin{aligned} y &= \mathrm{e}^{\int \frac{2}{x} \mathrm{d}x}\left( \int \frac{1}{2}x \mathrm{e}^{-\int \frac{2}{x} \mathrm{d}x} \mathrm{d}x + C \right)\\ &= x^2 \left( \int \frac{1}{2}x \frac{1}{x^2} \mathrm{d}x + C \right)\\ &= x^2 \left( \frac{1}{2}\ln|x| + C \right) \end{aligned}$$

形如

$$\frac{\mathrm{d}y}{\mathrm{d}x} = p(x)y + q(x)y^n \quad (n \neq 0, 1)$$

的方程称为伯努利（Bernoulli）微分方程。

求解过程： 将方程两端除以 $y^n$，得到

$$y^{-n} \frac{\mathrm{d}y}{\mathrm{d}x} = p(x)y^{1 - n} + q(x)$$

令 $z = y^{1 - n}$，则有

$$(1 - y)y^{-n} \frac{\mathrm{d}y}{\mathrm{d}x} = \frac{\mathrm{d}z}{\mathrm{d}x}$$

代入方程，可得

$$\frac{1}{1 - n} \frac{\mathrm{d}z}{\mathrm{d}x} = p(x)z + q(x)$$

即

$$\frac{\mathrm{d}z}{\mathrm{d}x} = (1 - n)p(x)z + (1 - n)q(x)$$

得到一阶线性微分方程，求出 $z$ 后再用 $y$ 代回，即可得到伯努利方程的解。

当 $n > 0$ 时，方程显然有解 $y = 0$，在求解时应该加上。

例：求解方程 $\dfrac{\mathrm{d}y}{\mathrm{d}x} + \dfrac{y}{x} = (\ln{x})y^2$.

解：这是一个 $n = 2$ 的伯努利方程，显然 $y = 0$ 是该方程的解。当 $y \neq 0$ 时，方程两端同时除以 $y^2$ 得

$$y^{-2}\frac{\mathrm{d}y}{\mathrm{d}x} + \frac{1}{x}y^{-1} = \ln{x}$$

令 $z = y^{-1}$，则有 $\dfrac{\mathrm{d}z}{\mathrm{d}x} = -y^{-2}\dfrac{\mathrm{d}y}{\mathrm{d}x}$.

于是原方程化为一阶线性微分方程

$$\dfrac{\mathrm{d}z}{\mathrm{d}x} = \dfrac{z}{x} -\ln{x}$$

令 $p(x) = \dfrac{1}{x}, q(x) = \ln{x}$，则通解为

$$\begin{aligned} z(x) &= \mathrm{e}^{\int \frac{1}{x} \mathrm{d}x} \left( \int \ln{x} \mathrm{e}^{-\int \frac{1}{x} \mathrm{d}x} \mathrm{d}x + C \right)\\ &= -\frac{1}{2} x \ln^2{x} + C_1 x \end{aligned}$$

将 $z = y^{-1}$ 代入上式，得到原方程的解为

$$y(x) = \frac{1}{x \left[ C - \dfrac{1}{2}(\ln{x})^2 \right]}$$

其中 $C$ 为任意常数。此外方程还有解 $y = 0$.

全微分方程和积分因子

形如

$$P(x, y)\mathrm{d}x + Q(x, y)\mathrm{d}y = 0$$

的一阶微分方程称为对称式微分方程，其中 $P(x, y), Q(x, y)$ 在单连通区域 $D$ 内有连续的一阶偏导数。如果方程的左端恰为一个二元函数 $u(x, y)$ 的全微分，即

$$\mathrm{d}u(x, y) = P(x, y)\mathrm{d}x + Q(x, y)\mathrm{d}y$$

则称该方程为全微分方程或恰当方程，而函数 $u(x, y)$ 称为微分式的原函数。

$$u(x, y) = C$$

就是全微分方程的隐式通解。

定理： 设函数 $P(x, y), Q(x, y)$ 在单连通区域 $D$ 内有连续的一阶偏导数，则 $P(x, y)\mathrm{d}x + Q(x, y)\mathrm{d}y = 0$ 为全微分方程的充要条件是

$$\frac{\partial P}{\partial y} \equiv \frac{\partial Q}{\partial x}$$

在 $D$ 内处处成立，对应的原函数为

$$u(x, y) = \int_{(x_0, y_0)}^{(x, y)} P(x, y)\mathrm{d}x + Q(x, y)\mathrm{d}y$$

其中 $(x_0, y_0)$ 为 $D$ 中任意一点。

此时，由方程

$$u(x, y) = \int_{(x_0, y_0)}^{(x, y)} P(x, y)\mathrm{d}x + Q(x, y)\mathrm{d}y = C$$

所确定的函数，就是全微分方程的隐式通解。

例：求解方程 $(x^3 + x^2 y^3)\mathrm{d}x + (x^3 + x^2 + y^3)\mathrm{d}y = 0$.

解：令 $P(x, y) = x^3 + x^2 y^3, Q(x, y) = x^3 + x^2 + y^3$，由于它们在 $Oxy$ 面上拥有连续的一阶偏导数，并且

$$\frac{\partial P}{\partial y} = \frac{\partial Q}{\partial x} = 3x^2 y^2$$

因此原方程为全微分方程。取 $x_0 = 0, y_0 = 0$，有

$$u(x, y) = \int_0^x x^3 \mathrm{d}x + \int_0^y (x^3 + x^2 + y^3) \mathrm{d}y = \frac{1}{4} x^4 + \frac{1}{3} x^3 y^3 + \frac{1}{4} y^4$$

从而

$$\frac{1}{4} x^4 + \frac{1}{3} x^3 y^3 + \frac{1}{4} y^4 = C$$

为原方程的隐式通解，其中 $C$ 为任意常数。

全微分初值问题

$$\begin{cases} P(x, y) \mathrm{d}x + Q(x, y) \mathrm{d}y = 0\\ y(x_0) = y_0 \end{cases}$$

的解为

$$u(x, y) = \int_{x_0}^x P(x, y_0) \mathrm{d}x + \int_{y_0}^y Q(x, y) \mathrm{d}y = 0$$

或

$$u(x, y) = \int_{x_0}^x P(x, y) \mathrm{d}x + \int_{y_0}^y Q(x_0, y) \mathrm{d}y = 0$$

积分因子： 设方程 $P(x, y)\mathrm{d}x + Q(x, y)\mathrm{d}y = 0$ 不是全微分方程，如果存在连续可微函数 $\mu(x, y) \neq 0$，使方程

$$\mu(x, y)P(x, y)\mathrm{d}x + \mu(x, y)Q(x, y)\mathrm{d}y = 0$$

成为全微分方程，则称 $\mu(x, y)$ 为原方程的积分因子。

方程有 $\mu = \mu(x)$ 型的积分因子的充要条件是函数

$$\frac{\dfrac{\partial P}{\partial y} - \dfrac{\partial Q}{\partial x}}{Q}$$

只是变量 $x$ 的函数，此时积分因子为

$$\mu(x) = \exp \left\{ \int \frac{1}{Q} \left( \dfrac{\partial P}{\partial y} - \dfrac{\partial Q}{\partial x} \right) \mathrm{d}x \right\}$$

方程有 $\mu = \mu(y)$ 型的积分因子的充要条件是函数

$$-\frac{\dfrac{\partial P}{\partial y} - \dfrac{\partial Q}{\partial x}}{P}$$

只是变量 $y$ 的函数，此时积分因子为

$$\mu(x) = \exp \left\{ -\int \frac{1}{P} \left( \dfrac{\partial P}{\partial y} - \dfrac{\partial Q}{\partial x} \right) \mathrm{d}x \right\}$$

一阶隐式方程

一阶隐式方程的一般形式为

$$F(x, y, y') = 0$$

情况 1： 在区间 $(\alpha, \beta)$ 上可微的函数 $x = \varphi(t), y = \psi(t)$，如果能使

$$F\left[ \varphi(t), \psi(t), \ \right] \equiv 0 \quad (\alpha < t < \beta)$$

则称函数 $x = \varphi(t), y = \psi(t)$ 是方程在 $(\alpha, \beta)$ 上的参数形式的解。

情况 2： 设方程已就 $y$ 解出

$$y = f(x, y')$$

并设函数 $f(x, y')$ 有连续的偏导数。

引入未知函数 $p = p(x) = y'$，则 $y= f(x, p)$. 两端关于 $x$ 求导得

$$p = f_x'(x, p) + f_p'(x, p)\frac{\mathrm{d}p}{\mathrm{d}x}$$

或写成对称形式

$$[p - f_x'(x, p)]\mathrm{d}x - f_p'(x, p)\mathrm{d}p = 0$$

若从上述方程中解出 $p = p(x, C)$，则代入 $y = f(x, p)$，可得原方程的通解为

$$y = f[x, p(x, C)]$$

若从上述方程中解出 $x = x(p, C)$，则得原方程的参数形式通解为

$$\begin{cases} x = x(p, C) \\ y = f[x(p, C), p] \end{cases}$$

若从上述方程中解出隐式通解 $\varPhi(x, p, C) = 0$，则得原方程的参数形式隐式通解为

$$\begin{cases} y = f(x, p) \\ \varPhi(x, p, C) = 0 \end{cases}$$

高阶微分方程

可降阶的高阶微分方程

1. 方程 $y^{(n)} = f(x)$

常微分方程

$$y^{(n)} = f(x)$$

的右端项 $f(x)$ 仅含有自变量 $x$. 两端积分，可得一个 $n - 1$ 阶的微分方程

$$y^{(n - 1)} = \int f(x) \mathrm{d}x + C_1$$

同理可得

$$y^{(n - 2)} = \int \left[ \int f(x) \mathrm{d}x + C_1 \right]\mathrm{d}x + C_2 = \iint f(x)(\mathrm{d}x)^2 + C_1x + C_2$$

所以通过 $n$ 次积分可求得方程的通解为

$$y = \underbrace{\int \cdots \int}_n f(x)(\mathrm{d}x)^n + \frac{C_1}{(n - 1)!} x^{n - 1} + \frac{C_2}{(n - 2)!} x^{n - 2} + \cdots + C_{n - 1}x + C_n$$

其中 $C_1, C_2, \cdots, C_n$ 为任意常数。

例：求微分方程 $y''' = x\mathrm{e}^x$ 的通解。

解：对所给方程两端依次积分三次，可得

$$\begin{aligned} y'' &= \int x\mathrm{e}^x \mathrm{d}x = \int x \mathrm{d}\mathrm{e}^x = x\mathrm{e}^x - \int \mathrm{e}^x \mathrm{d}x = (x - 1)\mathrm{e}^x + C\\ y' &= \int (x - 1)\mathrm{e}^x \mathrm{d}x + Cx + C_2 = (x - 2)\mathrm{e}^x + Cx + C_2\\ y &= \int (x - 2)\mathrm{e}^x \mathrm{d}x + \frac{C}{2}x^2 + C_2 x + C_3\\ &= (x - 3)\mathrm{e}^x + C_1x^2 + C_2x + C_3 \quad (C_1 = \frac{C}{2}) \end{aligned}$$

其中 $C_1, C_2, C_3$ 为任意常数。

2. 方程 $y'' = f(x, y')$

常微分方程

$$y'' = f(x, y')$$

不显式地含有 $y$. 令 $y' = p$，则 $y'' = \dfrac{\mathrm{d}p}{\mathrm{d}x} = p'$，于是原方程化为

$$p' = f(x, p)$$

设其通解为 $p = \varphi(x, C_1)$，即 $y' = \varphi(x, C_1)$. 两端积分可得原方程的通解为

$$y = \int \varphi(x, C_1) \mathrm{d}x + C_2$$

其中 $C_1, C_2$ 为任意常数。

例：求微分方程 $xy'' + y' - x^2$ 的通解。

解：令 $y' = p$，则原方程化为 $xp' + p - x^2 = 0$，即 $p' = -\dfrac{p}{x} + x$.

先解 $p' = -\dfrac{p}{x}$，其通解为 $p = \dfrac{C}{x}$.

令 $p = \dfrac{C(x)}{x}$ 为方程 $p' = -\dfrac{p}{x} + x$ 的解，则 $\dfrac{C'(x)}{x} = x$，从而 $C'(x) = x^2$，于是 $C(x) = \dfrac{1}{3}x^3 + C$，因此

$$y' = \frac{\dfrac{1}{3}x^3 + C}{x} = \frac{1}{3}x^2 + \frac{C_1}{x}$$

则原方程的通解为

$$y = \frac{1}{9}x^3 + C_1 \ln|x| + C_2$$

其中 $C_1, C_2$ 为任意常数。

3. 方程 $y'' = f(y, y')$

常微分方程

$$y'' = f(x, y')$$

不显式地含有 $x$. 令 $y' = p$，则 $y'' = \dfrac{\mathrm{d}p}{\mathrm{d}x} = \dfrac{\mathrm{d}p}{\mathrm{d}y} \cdot \dfrac{\mathrm{d}y}{\mathrm{d}x} = p\dfrac{\mathrm{d}p}{\mathrm{d}y}$，于是原方程化为

$$p\frac{\mathrm{d}p}{\mathrm{d}y} = f(y, p)$$

设其通解为 $p = \varphi(y, C_1)$，即 $y' = \varphi(y, C_1)$，则分离变量后积分得

$$\int \frac{\mathrm{d}y}{\varphi(y, C_1)} = x + C_2$$

即为原方程的通解，其中 $C_1, C_2$ 为任意常数。

例：求微分方程 $y y'' - (y')^2 = 0$ 的通解。

解：令 $y' = p$，将它及 $y'' = p\dfrac{\mathrm{d}p}{\mathrm{d}y}$ 代入所给方程中得

$$yp\frac{\mathrm{d}p}{\mathrm{d}y} - p^2 = 0$$

当 $y \neq 0, p \neq 0$ 时，约去 $p$ 并分离变量得

$$\frac{\mathrm{d}p}{p} = \frac{\mathrm{d}y}{y}$$

两端积分得 $\ln|p| = \ln|y| + C$，即 $p = C_1 y$，也就是

$$y' = C_1 y \quad (C_1 = \pm \mathrm{e}^C)$$

分离变量后两端再积分得

$$\ln|y| = C_1 x + C_2'$$

则

$$y = C_2 \mathrm{e}^{C_1 x} \quad (C_2 = \pm \mathrm{e}^{C_2'})$$

当 $p = 0$ 时，即 $y' = 0$ 时，$y = C$（$C$ 为任意常数）为所给方程的解，而 $y = 0$ 也为所给方程的解，从而所给方程的通解为

$$y = C_2 \mathrm{e}^{C_1 x}$$

其中 $C_1, C_2$ 为任意常数。

高阶齐次线性微分方程

$n$ 阶线性微分方程的一般形式为

$$y^{(n)} + p_1(x) y^{(n - 1)} + \cdots + p_{n - 1}(x)y' + p_n(x)y = f(x)$$

其中 $p_1(x), \cdots, p_{n - 1}(x),p_n(x), f(x)$ 为关于 $x$ 的已知函数。当 $f(x) \equiv 0$ 时，称此方程为 $\bm{n}$ 阶齐次线性微分方程；当 $f(x) \not\!\equiv 0$ 时，称此方程为 $\bm{n}$ 阶非齐次线性微分方程。

通解的结构：

定义： 设 $y_1(x), y_2(x), \cdots, y_n(x)$ 是定义在区间 $I$ 上的 $n$ 个函数，若存在 $n$ 个不全为零的常数 $k_1, k_2, \cdots, k_n$，使得当 $x \in I$ 时有恒等式

$$k_1 y_1(x) + k_2 y_2(x) + \cdots + k_n y_n(x) \equiv 0$$

成立，则称这 $n$ 个函数在区间 $I$ 上线性相关，否则称为线性无关。

如果两个函数的比是常数，则它们就是线性相关的；否则，就是线性无关的。

定理： 若函数 $y_1(x)$ 和 $y_2(x)$ 是二阶齐次线性微分方程 $y'' + p_1(x)y' + p_2(x)y = 0$ 的两个线性无关的解，则它们的线性组合

$$y(x) = C_1 y_1(x) + C_2 y_2(x)$$

是该方程的通解，其中 $C_1, C_2$ 为任意常数。

推论： 若函数 $y_1(x), y_2(x), \cdots, y_n(x)$ 是 $n$ 阶齐次线性微分方程

$$y^{(n)} + p_1(x)y^{(n - 1)} + \cdots + p_{n - 1}(x)y' + p_n(x)y = 0$$

的 $n$ 个线性无关的解，则它们的线性组合

$$y(x) = C_1 y_1(x) + C_2 y_2(x) + \cdots + C_n y_n(x)$$

是该方程的通解，其中 $C_1, C_2, \cdots, C_n$ 为任意常数。

通解的求法：

（1）置换法

例：已知函数 $y_1(x) = \mathrm{e}^{2x}$ 是方程

$$(x + 2)y'' - (2x + 5)y' + 2y = 0$$

的解，求此方程的通解。

解：令 $y_2(x) = u(x)\mathrm{e}^{2x}$ 为所给方程的另一个解，将其代入方程中得

$$(x + 2)[u''(x)\mathrm{e}^{2x} + 4u'(x)\mathrm{e}^{2x} + 4u(x)\mathrm{e}^{2x}] - (2x + 5)[u'(x)\mathrm{e}^{2x} + 2u(x)\mathrm{e}^{2x}] + 2u(x)\mathrm{e}^{2x} = 0$$

整理得

$$(x + 2)u'' + (2x + 3)u' = 0$$

令 $v(x) = u'(x)$，则 $v(x)$ 满足方程 $(x + 2)v' + (2x + 3)v = 0$，分离变量得

$$\frac{\mathrm{d}v}{v} = -\frac{2x + 3}{x + 2}\mathrm{d}x$$

两端积分得

$$\ln|v| = -2x + \ln(x + 2) + C_1$$

即

$$v(x) = C(x + 2)\mathrm{e}^{-2x}$$

取 $C = 1$，$v(x) = (x + 2)\mathrm{e}^{-2x}$，从而

$$u'(x) = (x + 2)\mathrm{e}^{-2x}$$

积分得

$$\begin{aligned} u(x) &= \int (x + 2)\mathrm{e}^{-2x}\mathrm{d}x = -\frac{1}{2}\int(x + 2)\mathrm{d}\mathrm{e}^{-2x}\\ &= -\frac{1}{2} \left[ (x + 2)\mathrm{e}^{-2x} - \int \mathrm{e}^{-2x}\mathrm{d}x \right]\\ &= -\frac{1}{2}(x + 2)\mathrm{e}^{-2x} - \frac{1}{4}\mathrm{e}^{-2x} = -\frac{1}{4}(2x + 5)\mathrm{e}^{-2x} \end{aligned}$$

故 $y_2(x) = u(x)\mathrm{e}^{2x} = -\dfrac{1}{4}(2x + 5)$，

于是所求通解为 $y(x) = C_1 \mathrm{e}^{2x} + \dfrac{C_2}{4}(2x + 5)$，其中 $C_1, C_2$ 为任意常数。

（2）幂级数解法

定理： 若方程 $y'' + p_1(x)y' + p_2(x)y = 0$ 的系数 $p_1(x), p_2(x)$ 在点 $x = 0$ 处于区间 $(-R, R)$ 内可展成幂级数，则该方程在 $(-R, R)$ 内有幂级数解

$$y(x) = a_0 + a_1 x + a_2 x^2 + \cdots + a_n x^n + \cdots, -R < x < R$$

常系数齐次线性微分方程：

在二阶齐次线性方程 $y'' + p_1(x)y' + p_2(x)y = 0$ 中，如果 $y', y$ 的系数 $p_1(x)$ 和 $p_2(x)$ 均为常数，即

$$y'' + p_1 y' + p_2 y = 0$$

其中 $p_1, p_2$ 为常数，则称该方程为二阶常系数齐次线性微分方程；否则，称其为二阶变系数齐次线性微分方程。

因为该方程关于 $y, y', y''$ 是齐次式，可设 $y = \mathrm{e}^{\alpha x}$ 为方程的解，其中 $\alpha$ 为待定常数。

将上式代入原方程中得

$$\mathrm{e}^{\alpha x}(\alpha^2 + p_1 \alpha + p_2) \equiv 0$$

因为 $\mathrm{e}^{\alpha x} \neq 0$，所以

$$\alpha^2 + p_1 \alpha + p_2 = 0$$

称 $\alpha^2 + p_1 \alpha + p_2 = 0$ 为常系数齐次线性微分方程的特征方程，该方程的根为特征根。

特征方程的特征根分为以下情况：

1. 若特征方程有两个互异实根 $\alpha_1, \alpha_2$，即 $p_1^2 - 4p_2 > 0$，则原方程的通解为

$$y(x) = C_1 \mathrm{e}^{\alpha_1 x} + C_2 \mathrm{e}^{\alpha_2 x}$$

2. 若特征方程有一对共轭复数根 $\alpha \pm \mathrm{i}\beta$，即 $p_1^2 - 4p_2 < 0$，则原方程的通解为

$$y(x) = C_1 \mathrm{e}^{\alpha x} \cos\beta x + C_2 \mathrm{e}^{\alpha x} \sin\beta x = \mathrm{e}^{\alpha x}(C_1 \cos\beta x + C_2 \sin\beta x)$$

3. 若特征方程有重根 $\alpha_1 = \alpha_2 = \alpha$，即 $p_1^2 - 4p_2 = 0$，则原方程的通解为

$$y(x) = C_1 \mathrm{e}^{\alpha x} + C_2 x\mathrm{e}^{\alpha x} = (C_1 + C_2 x)\mathrm{e}^{\alpha x}$$

上述二阶常系数齐次线性微分方程的求解方法也适用于 $n\ (n > 2)$ 阶常系数齐次线性微分方程

$$y^{(n)} + p_1 y^{(n - 1)} + \cdots + p_{n - 1} y' + p_n y = 0$$

其中 $p_1, p_2, \cdots, p_n$ 为常数。对应的特征方程

$$\alpha^n + p_1 \alpha^{n - 1} + \cdots + p_{n - 1} \alpha + p_n = 0$$

的特征根 $\alpha_1, \alpha_2, \cdots, \alpha_n$ 分为以下情况：

1. 特征根都是单根，且都是实数，则方程的通解为

$$y(x) = C_1 \mathrm{e}^{\alpha_1 x} + C_2 \mathrm{e}^{\alpha_2 x} + \cdots + C_n \mathrm{e}^{\alpha_n x}$$

2. 特征根都是单根，但其中有复根，则复根应成对出现。不妨设 $\alpha_1 = \alpha + \mathrm{i}\beta, \alpha_2 = \alpha - \mathrm{i}\beta$ 是共轭复根，其余的 $\alpha_3, \alpha_4, \cdots, \alpha_n$ 为实根，则方程的通解为

$$y(x) = C_1 \mathrm{e}^{\alpha x}\cos{\beta x} + C_2 \mathrm{e}^{\alpha x}\sin{\beta x} + C_3 \mathrm{e}^{\alpha_3 x} + \cdots + C_n \mathrm{e}^{\alpha_n x}$$

3. 特征根中有重根，设 $\alpha_1 = \alpha_2 = \cdots = \alpha_k$ 是 $k$ 重根，$\alpha_{k + 1}, \cdots, \alpha_n$ 是单根，则方程的通解为

$$y(x) = (C_1 + C_2 x + \cdots + C_k x^{k - 1})\mathrm{e}^{\alpha_1 x} + C_{k + 1} \mathrm{e}^{\alpha_{k + 1} x} + \cdots + C_n \mathrm{e}^{\alpha_n x}$$

高阶非齐次线性微分方程

通解的结构：

定理： 若函数 $y^*(x)$ 是二阶非齐次线性微分方程 $y'' + p_1(x)y' + p_2(x)y = f(x)$ 的一个特解，函数 $Y(x)$ 是该方程对应的齐次方程 $y'' + p_1(x)y' + p_2(x)y = 0$ 的通解，则函数

$$y(x) = Y(x) + y^*(x)$$

是该方程的通解。

此定理说明二阶非齐次线性微分方程的通解等于其对应的齐次方程的通解与其一个特解之和。

此结论也可以推广到 $n\ (n > 2)$ 阶非齐次线性微分方程。

叠加原理： 设二阶非齐次线性微分方程的右端项 $f(x)$ 是两个函数之和，即

$$y'' + p_1(x)y' + p_2(x)y = f_1(x) + f_2(x)$$

而函数 $y_1^*(x)$ 与 $y_2^*(x)$ 分别是方程

$$y'' + p_1(x)y' + p_2(x)y = f_1(x), \quad y'' + p_1(x)y' + p_2(x)y = f_2(x)$$

的特解，则函数 $y_1^*(x) + y_2^*(x)$ 是原方程的特解。

通解的求法：

设二阶非齐次线性微分方程 $y'' + p_1(x)y' + p_2(x)y = f(x)$ 对应的齐次方程 $y'' + p_1(x)y' + p_2(x)y = 0$ 的通解为

$$Y(x) = C_1 y_1(x) + C_2 y_2(x)$$

利用常数变易法，设二阶非齐次线性微分方程有解

$$y(x) = C_1(x) y_1(x) + C_2(x) y_2(x)$$

选择 $C_1(x), C_2(x)$ 使得

$$C_1'(x) y_1(x) + C_2'(x) y_2(x) = 0$$

此时有

$$C_1'(x) y_1'(x) + C_2'(x) y_2'(x) = f(x)$$

则二阶非齐次线性微分方程的通解为

$$y(x) = C_1 y_1(x) + C_2 y_2(x) - y_1(x) \int\frac{y_2(x)f(x)}{W(x)}\mathrm{d}x + y_2(x) \int\frac{y_1(x)f(x)}{W(x)}\mathrm{d}x$$

其中 $W(x)$ 为系数行列式

$$W(x) = \begin{vmatrix} y_1(x) & y_2(x) \\ y_1'(x) & y_2'(x) \end{vmatrix} \neq 0$$

对于一般的 $n\ (n > 2)$ 阶非齐次线性微分方程，有相同的求解方法。若

$$Y(x) = C_1 y_1(x) + C_2 y_2(x) + \cdots + C_n y_n(x)$$

为方程所对应的齐次方程的通解，其中 $C_1, C_2, \cdots, C_n$ 是任意常数。利用常数变易法，设原方程有解

$$y(x) = C_1(x) y_1(x) + C_2(x) y_2(x) + \cdots + C_n y_n(x)$$

可确定 $C_1(x), C_2(x), \cdots, C_n(x)$ 应满足下列 $n$ 个方程

$$\begin{cases} C_1'(x) y_1(x) + C_2'(x) y_2(x) + \cdots + C_n'(x) y_n(x) = 0, \\ C_1'(x) y_1'(x) + C_2'(x) y_2'(x) + \cdots + C_n'(x) y_n'(x) = 0, \\ \cdots \\ C_1'(x) y_1^{(n - 2)}(x) + C_2'(x) y_2^{(n - 2)}(x) + \cdots + C_n'(x) y_n^{(n - 2)}(x) = 0, \\ C_1'(x) y_1^{(n - 1)}(x) + C_2'(x) y_2^{(n - 1)}(x) + \cdots + C_n'(x) y_n^{(n - 1)}(x) = 0, \\ \end{cases}$$

它是关于变量 $C_i'(x)\ (i = 1, 2, \cdots, n)$ 的线性方程组，解出 $C_i'(x)$ 后再积分便得 $C_i(x)$，代入 $y(x) = C_1(x) y_1(x) + C_2(x) y_2(x) + \cdots + C_n y_n(x)$ 即可得到非齐次线性微分方程的通解。

常系数非齐次线性微分方程：

1. $f(x) = R_m(x)\mathrm{e}^{\lambda x}$ 型： 方程

$$y'' +p_1 y' + p_2 y = R_m(x)\mathrm{e}^{\lambda x}$$

具有形如

$$y^*(x) = x^k Q_m(x)\mathrm{e}^{\lambda x}$$

的特解，其中 $Q_m(x)$ 是与 $R_m(x)$ 同次的多项式，且

$$Q_m''(x) + (2\lambda + p_1)Q_m'(x) + (\lambda^2 + p_1\lambda + p_2)Q_m(x) \equiv R_m(x)$$

而 $k$ 按 $\lambda$ 不是特征方程 $\alpha^2 + p_1\alpha + p_2 = 0$ 的根、是单根和是二重根依次取为 $0, 1, 2$.

2. $f(x) = \mathrm{e}^{\lambda x}[R_l(x)\cos{\omega x} + R_n(x)\sin{\omega x}]$ 型： 方程

$$y'' + p_1 y' + p_2 y = \mathrm{e}^{\lambda x}[R_l(x)\cos{\omega x} + R_n(x)\sin{\omega x}]$$

具有形如

$$y^*(x) = x^k \mathrm{e}^{\lambda x}[Q_m'(x)\cos{\omega x} + Q_m''(x)\sin{\omega x}]$$

的特解，其中 $Q_m'(x), Q_m''(x)$ 是 $m$ 次多项式，$m = \max{l, n}$，而 $k$ 按 $\lambda \pm \mathrm{i}\omega$ 不是特征方程 $\alpha^2 + p_1\alpha + p_2 = 0$ 的根、是单根和是二重根依次取为 $0, 1, 2$.

欧拉方程

欧拉方程是一种特殊的变系数线性微分方程，其形式如下

$$x^n y^{(n)} + p_1 x^{n - 1} y^{(n - 1)} + \cdots + p_{n - 1} xy' + p_n y = f(x)$$

其中 $p_1, p_2, \cdots, p_n$ 为常数，$f(x)$ 为已知函数。该方程可经变换化成常系数线性微分方程，因而容易求解。

转化方式： 令 $x = \mathrm{e}^t$，即 $t = \ln{x}$，注意到

$$\begin{aligned} \frac{\mathrm{d}y}{\mathrm{d}x} &= \frac{1}{x}\frac{\mathrm{d}y}{\mathrm{d}t}\\ \frac{\mathrm{d}^2 y}{\mathrm{d}x^2} &= \frac{1}{x^2}\left( \frac{\mathrm{d}^2 y}{\mathrm{d}t^2} - \frac{\mathrm{d}y}{\mathrm{d}t} \right),\\ \frac{\mathrm{d}^3 y}{\mathrm{d}x^3} &= \frac{1}{x^3}\left( \frac{\mathrm{d}^3 y}{\mathrm{d}t^3} - 3\frac{\mathrm{d}^2 y}{\mathrm{d}t^2} + 2\frac{\mathrm{d}y}{\mathrm{d}t} \right) \end{aligned}$$

如果用 $D$ 表示对 $t$ 的求导运算符号，即 $D = \dfrac{\mathrm{d}}{\mathrm{d}t}$，则有

$$\begin{aligned} xy' &= Dy,\\ x^2 y'' &= (D^2 - D)y,\\ x^3 y''' &= (D^3 - 3D^2 + 2D)y = D(D - 1)(D - 2)y \end{aligned}$$

一般地，有

$$x^n y^{(n)} = D(D - 1)(D - 2) \cdots (D - (n - 1))y$$

因此，欧拉方程可化为

$$D(D - 1)(D - 2) \cdots (D - (n - 1))y + p_1 D(D - 1)(D - 2)\\ \cdots (D - (n - 2))y + \cdots + p_{n - 1} Dy + p_n y = f(\mathrm{e}^t)$$

例：将微分方程 $x^3 y''' + x^2 y'' - 4xy' = x^3$ 转换为常系数线性微分方程。

解：令 $x = \mathrm{e}^t$，原方程可以化为

$$\begin{aligned} D(D - 1)(D - 2)y + D(D - 1)y - 4Dy &= \mathrm{e}^{3t}\\ (D^3 - 2D^2 - 3D)y &= \mathrm{e}^{3t} \end{aligned}$$

即

$$\frac{\mathrm{d}^3 y}{\mathrm{d}t^3} - 2\frac{\mathrm{d}^2 y}{\mathrm{d}t^2} - 3\frac{\mathrm{d}y}{\mathrm{d}t} = \mathrm{e}^{3t}$$