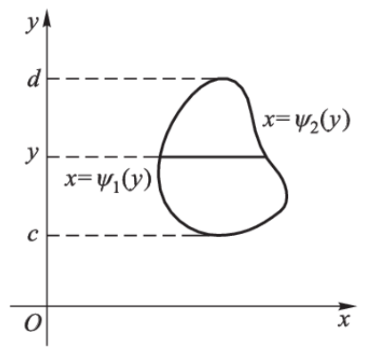二重积分
设 f ( x , y ) f(x,y) f ( x , y ) D D D D D D n n n
T = { Δ σ 1 . Δ σ 2 , ⋯ , Δ σ n } T=\{\Delta\sigma_1.\Delta\sigma_2,\cdots,\Delta\sigma_n\}
T = { Δ σ 1 .Δ σ 2 , ⋯ , Δ σ n }
其中 Δ σ i \Delta\sigma_i Δ σ i i i i Δ σ i \Delta\sigma_i Δ σ i Δ σ j \Delta\sigma_j Δ σ j ( ξ i , η i ) ∈ Δ σ i (\xi_i,\eta_i)\in\Delta\sigma_i ( ξ i , η i ) ∈ Δ σ i
∑ i = 1 n f ( ξ i , η i ) Δ σ i \sum_{i=1}^nf(\xi_i,\eta_i)\Delta\sigma_i
i = 1 ∑ n f ( ξ i , η i ) Δ σ i
以 d i d_i d i Δ σ i \Delta\sigma_i Δ σ i
∣ ∣ T ∣ ∣ = max 1 ≤ i ≤ n { d i } ||T||=\max\limits_{1\leq i\leq n}\{d_i\}
∣∣ T ∣∣ = 1 ≤ i ≤ n max { d i }
如果当 ∣ ∣ T ∣ ∣ → 0 ||T||\to 0 ∣∣ T ∣∣ → 0
lim ∣ ∣ T ∣ ∣ → 0 ∑ i = 1 n f ( ξ i , η i ) Δ σ i \lim_{||T||\to 0}\sum_{i=1}^nf(\xi_i,\eta_i)\Delta\sigma_i
∣∣ T ∣∣ → 0 lim i = 1 ∑ n f ( ξ i , η i ) Δ σ i
存在,并且这个极限与区域的分割方法及点 ( ξ i , η i ) (\xi_i,\eta_i) ( ξ i , η i ) f ( x , y ) f(x,y) f ( x , y ) D D D 可积的 ,并称此极限为函数 f ( x , y ) f(x,y) f ( x , y ) D D D 二重积分(double integral) ,记作
∬ D f ( x , y ) d σ = lim ∣ ∣ T ∣ ∣ → 0 ∑ i = 1 n f ( ξ i , η i ) Δ σ i \iint\limits_D f(x,y)\mathrm{d}\sigma=\lim_{||T||\to 0}\sum_{i=1}^nf(\xi_i,\eta_i)\Delta\sigma_i
D ∬ f ( x , y ) d σ = ∣∣ T ∣∣ → 0 lim i = 1 ∑ n f ( ξ i , η i ) Δ σ i
在直角坐标系中,面积元素 d σ = d x d y \mathrm{d}\sigma=\mathrm{d}x\mathrm{d}y d σ = d x d y
∬ D f ( x , y ) d x d y \iint\limits_D f(x,y)\mathrm{d}x\mathrm{d}y
D ∬ f ( x , y ) d x d y
若函数 f ( x , y ) f(x,y) f ( x , y ) D D D D D D
二重积分的几何意义:
如果被积函数 f ( x , y ) ≥ 0 f(x,y)\geq 0 f ( x , y ) ≥ 0 D D D ∬ D f ( x , y ) d σ \displaystyle\iint\limits_D f(x,y)\mathrm{d}\sigma D ∬ f ( x , y ) d σ z = f ( x , y ) z=f(x,y) z = f ( x , y ) D D D
二重积分的性质
性质 1: 如果 f ( x , y ) f(x,y) f ( x , y ) D D D k k k k f ( x , y ) kf(x,y) k f ( x , y ) D D D
∬ D k f ( x , y ) d σ = k ∬ D f ( x , y ) d σ \iint\limits_D kf(x,y)\mathrm{d}\sigma=k\iint\limits_D f(x,y)\mathrm{d}\sigma
D ∬ k f ( x , y ) d σ = k D ∬ f ( x , y ) d σ
即被积函数中的常数因子可以提到积分号外面。
性质 2: 如果 f ( x , y ) f(x,y) f ( x , y ) g ( x , y ) g(x,y) g ( x , y ) D D D f ( x , y ) ± g ( x , y ) f(x,y)\pm g(x,y) f ( x , y ) ± g ( x , y ) D D D
∬ D [ f ( x , y ) ± g ( x , y ) ] d σ = ∬ D f ( x , y ) d σ ± ∬ D g ( x , y ) d σ \iint\limits_D [f(x,y)\pm g(x,y)]\mathrm{d}\sigma=\iint\limits_D f(x,y)\mathrm{d}\sigma\pm\iint\limits_D g(x,y)\mathrm{d}\sigma
D ∬ [ f ( x , y ) ± g ( x , y )] d σ = D ∬ f ( x , y ) d σ ± D ∬ g ( x , y ) d σ
即函数代数和的二重积分等于每个函数的二重积分的代数和。
性质 3: 设有界闭区域 D = D 1 ∪ D 2 D=D_1\cup D_2 D = D 1 ∪ D 2 D 1 D_1 D 1 D 2 D_2 D 2 f ( x , y ) f(x,y) f ( x , y ) D 1 , D 2 D_1,D_2 D 1 , D 2 f ( x , y ) f(x,y) f ( x , y ) D D D
∬ D f ( x , y ) d σ = ∬ D 1 f ( x , y ) d σ + ∬ D 2 f ( x , y ) d σ \iint\limits_D f(x,y)\mathrm{d}\sigma=\iint\limits_{D_1} f(x,y)\mathrm{d}\sigma+\iint\limits_{D_2} f(x,y)\mathrm{d}\sigma
D ∬ f ( x , y ) d σ = D 1 ∬ f ( x , y ) d σ + D 2 ∬ f ( x , y ) d σ
即二重积分对于积分区域具有可加性。
性质 4: 若 σ \sigma σ D D D
∬ D d σ = σ \iint\limits_D\mathrm{d}\sigma=\sigma
D ∬ d σ = σ
性质 5: 如果 f ( x , y ) f(x,y) f ( x , y ) g ( x , y ) g(x,y) g ( x , y ) D D D f ( x , y ) ≤ g ( x , y ) f(x,y)\leq g(x,y) f ( x , y ) ≤ g ( x , y )
∬ D f ( x , y ) d σ ≤ ∬ D g ( x , y ) d σ \iint\limits_D f(x,y)\mathrm{d}\sigma\leq\iint\limits_D g(x,y)\mathrm{d}\sigma
D ∬ f ( x , y ) d σ ≤ D ∬ g ( x , y ) d σ
并且
∣ ∬ D f ( x , y ) d σ ∣ ≤ ∬ D ∣ f ( x , y ) ∣ d σ \left|\iint\limits_D f(x,y)\mathrm{d}\sigma\right|\leq\iint\limits_D|f(x,y)|\mathrm{d}\sigma
D ∬ f ( x , y ) d σ ≤ D ∬ ∣ f ( x , y ) ∣ d σ
估值定理: 设 f ( x , y ) f(x,y) f ( x , y ) D D D M , m M,m M , m f ( x , y ) f(x,y) f ( x , y ) D D D σ \sigma σ D D D
m σ ≤ ∬ D f ( x , y ) d σ ≤ M σ m\sigma\leq\iint\limits_D f(x,y)\mathrm{d}\sigma\leq M\sigma
mσ ≤ D ∬ f ( x , y ) d σ ≤ M σ
二重积分的中值定理: 设函数 f ( x , y ) f(x,y) f ( x , y ) D D D σ \sigma σ D D D ∃ ( ξ , η ) ∈ D \exists(\xi,\eta)\in D ∃ ( ξ , η ) ∈ D
∬ D f ( x , y ) d σ = f ( ξ , η ) σ \iint\limits_D f(x,y)\mathrm{d}\sigma=f(\xi,\eta)\sigma
D ∬ f ( x , y ) d σ = f ( ξ , η ) σ
证明:
由于 f ( x , y ) f(x,y) f ( x , y ) D D D m m m M M M
m σ ≤ ∬ D f ( x , y ) d σ ≤ M σ m\sigma\leq\iint\limits_D f(x,y)\mathrm{d}\sigma\leq M\sigma
mσ ≤ D ∬ f ( x , y ) d σ ≤ M σ
同时除以 σ \sigma σ
m ≤ 1 σ ∬ D f ( x , y ) d σ ≤ M m\leq\frac 1 \sigma\iint\limits_D f(x,y)\mathrm{d}\sigma\leq M
m ≤ σ 1 D ∬ f ( x , y ) d σ ≤ M
由介值定理得,在 D D D ( ξ , η ) (\xi,\eta) ( ξ , η )
f ( ξ , η ) = 1 σ ∬ D f ( x , y ) d σ f(\xi,\eta)=\frac 1 \sigma\iint\limits_D f(x,y)\mathrm{d}\sigma
f ( ξ , η ) = σ 1 D ∬ f ( x , y ) d σ
于是
∬ D f ( x , y ) d σ = f ( ξ , η ) σ \iint\limits_D f(x,y)\mathrm{d}\sigma=f(\xi,\eta)\sigma
D ∬ f ( x , y ) d σ = f ( ξ , η ) σ
二重积分中值定理的几何意义:当 f ( x , y ) ≥ 0 f(x,y)\geq 0 f ( x , y ) ≥ 0 f ( x , y ) f(x,y) f ( x , y ) D D D D D D ( ξ , η ) (\xi,\eta) ( ξ , η ) f ( ξ , η ) f(\xi,\eta) f ( ξ , η ) D D D
直角坐标系下的二重积分
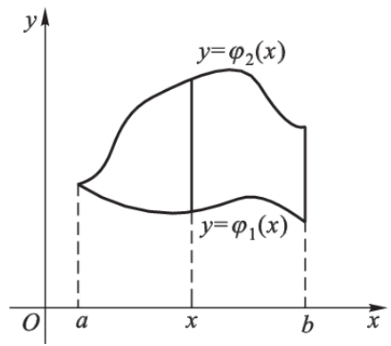
我们称形如
D = { ( x , y ) ∣ φ 1 ( x ) ≤ y ≤ φ 2 ( x ) , a ≤ x ≤ b } D=\{(x,y)\mid \varphi_1(x)\leq y\leq\varphi_2(x),a\leq x\leq b\}
D = {( x , y ) ∣ φ 1 ( x ) ≤ y ≤ φ 2 ( x ) , a ≤ x ≤ b }
的闭区域为 x \bm x x 型区域 ,其中 φ 1 ( x ) , φ 2 ( x ) \varphi_1(x),\varphi_2(x) φ 1 ( x ) , φ 2 ( x ) [ a , b ] [a,b] [ a , b ]
我们称形如
D = { ( x , y ) ∣ ψ 1 ( x ) ≤ y ≤ ψ 2 ( x ) , c ≤ y ≤ d } D=\{(x,y)\mid \psi_1(x)\leq y\leq\psi_2(x),c\leq y\leq d\}
D = {( x , y ) ∣ ψ 1 ( x ) ≤ y ≤ ψ 2 ( x ) , c ≤ y ≤ d }
的闭区域为 y \bm y y 型区域 ,其中 ψ 1 ( x ) , ψ 2 ( x ) \psi_1(x),\psi_2(x) ψ 1 ( x ) , ψ 2 ( x ) [ c , d ] [c,d] [ c , d ]
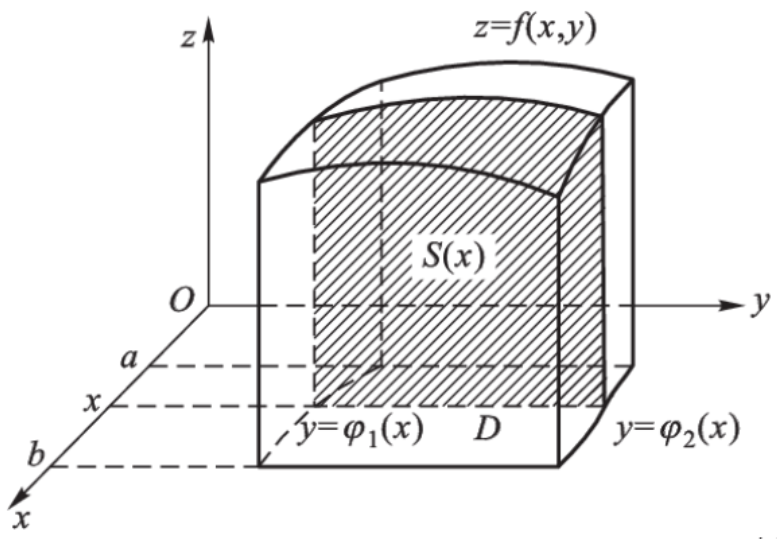
现有一以 D D D z = f ( x , y ) z=f(x,y) z = f ( x , y ) ∬ D f ( x , y ) d σ \displaystyle\iint\limits_D f(x,y)\mathrm{d}\sigma D ∬ f ( x , y ) d σ
设 D D D x x x [ a , b ] [a,b] [ a , b ] x 0 x_0 x 0 ( x 0 , 0 , 0 ) (x_0,0,0) ( x 0 , 0 , 0 ) O y z Oyz O yz x = x 0 x=x_0 x = x 0 S ( x 0 ) S(x_0) S ( x 0 ) [ φ 1 ( x 0 ) , φ 2 ( x 0 ) ] [\varphi_1(x_0),\varphi_2(x_0)] [ φ 1 ( x 0 ) , φ 2 ( x 0 )] z = f ( x 0 , y ) z=f(x_0,y) z = f ( x 0 , y )
S ( x 0 ) = ∫ φ 1 ( x 0 ) φ 2 ( x 0 ) f ( x 0 , y ) d y S(x_0)=\int_{\varphi_1(x_0)}^{\varphi_2(x_0)}f(x_0,y)\mathrm{d}y
S ( x 0 ) = ∫ φ 1 ( x 0 ) φ 2 ( x 0 ) f ( x 0 , y ) d y
体积可以表示为
V = ∫ a b S ( x ) d x = ∫ a b [ ∫ φ 1 ( x 0 ) φ 2 ( x 0 ) f ( x 0 , y ) d y ] d x V=\int_a^bS(x)\mathrm{d}x=\int_a^b\left[\int_{\varphi_1(x_0)}^{\varphi_2(x_0)}f(x_0,y)\mathrm{d}y\right]\mathrm{d}x
V = ∫ a b S ( x ) d x = ∫ a b [ ∫ φ 1 ( x 0 ) φ 2 ( x 0 ) f ( x 0 , y ) d y ] d x
所以
∬ D f ( x , y ) d x d y = ∫ a b [ ∫ φ 1 ( x 0 ) φ 2 ( x 0 ) f ( x 0 , y ) d y ] d x = ∫ a b d x ∫ φ 1 ( x ) φ 2 ( x ) f ( x , y ) d y \begin{aligned}
\iint\limits_D f(x,y)\mathrm{d}x\mathrm{d}y&=\int_a^b\left[\int_{\varphi_1(x_0)}^{\varphi_2(x_0)}f(x_0,y)\mathrm{d}y\right]\mathrm{d}x\\
&=\int_a^b\mathrm{d}x\int_{\varphi_1(x)}^{\varphi_2(x)}f(x,y)\mathrm{d}y
\end{aligned} D ∬ f ( x , y ) d x d y = ∫ a b [ ∫ φ 1 ( x 0 ) φ 2 ( x 0 ) f ( x 0 , y ) d y ] d x = ∫ a b d x ∫ φ 1 ( x ) φ 2 ( x ) f ( x , y ) d y
这个公式成功将二重积分转化为了先对 y y y x x x 累次积分(iterated integral) 。
同理可得,当 D D D y y y x x x y y y
∬ D f ( x , y ) d x d y = ∫ c d d y ∫ ψ 1 ( y ) ψ 2 ( y ) f ( x , y ) d x \iint\limits_D f(x,y)\mathrm{d}x\mathrm{d}y=\int_c^d\mathrm{d}y\int_{\psi_1(y)}^{\psi_2(y)}f(x,y)\mathrm{d}x
D ∬ f ( x , y ) d x d y = ∫ c d d y ∫ ψ 1 ( y ) ψ 2 ( y ) f ( x , y ) d x
当 D D D x x x y y y D D D x x x y y y
当 D D D x x x y y y
∫ a b d x ∫ φ 1 ( x ) φ 2 ( x ) f ( x , y ) d y = ∫ c d d y ∫ ψ 1 ( y ) ψ 2 ( y ) f ( x , y ) d x \int_a^b\mathrm{d}x\int_{\varphi_1(x)}^{\varphi_2(x)}f(x,y)\mathrm{d}y=\int_c^d\mathrm{d}y\int_{\psi_1(y)}^{\psi_2(y)}f(x,y)\mathrm{d}x
∫ a b d x ∫ φ 1 ( x ) φ 2 ( x ) f ( x , y ) d y = ∫ c d d y ∫ ψ 1 ( y ) ψ 2 ( y ) f ( x , y ) d x
例:计算 ∬ D x 2 y 2 d x d y \displaystyle\iint\limits_D\frac{x^2}{y^2}\mathrm{d}x\mathrm{d}y D ∬ y 2 x 2 d x d y D D D x y = 1 xy=1 x y = 1 y = x y=x y = x x = 2 x=2 x = 2
解:将 D D D y y y y = 1 y=1 y = 1 D D D D 1 , D 2 D_1,D_2 D 1 , D 2
D 1 : 1 y ≤ x ≤ 2 , 1 2 ≤ y ≤ 1 D 2 : y ≤ x ≤ 2 , 1 ≤ y ≤ 2 D_1:\quad\frac 1 y\leq x\leq 2,\quad \frac 1 2\leq y\leq 1\\
D_2:\quad y\leq x\leq 2,\quad 1\leq y\leq 2 D 1 : y 1 ≤ x ≤ 2 , 2 1 ≤ y ≤ 1 D 2 : y ≤ x ≤ 2 , 1 ≤ y ≤ 2
则
∬ D x 2 y 2 d x d y = ∬ D 1 x 2 y 2 d x d y + ∬ D 2 x 2 y 2 d x d y = ∫ 1 2 1 1 y 2 d y ∫ 1 y 2 x 2 d x + ∫ 1 2 1 y 2 d y ∫ y 2 x 2 d x = 9 4 \begin{aligned}
\iint\limits_D\frac{x^2}{y^2}\mathrm{d}x\mathrm{d}y&=\iint\limits_{D_1}\frac{x^2}{y^2}\mathrm{d}x\mathrm{d}y+\iint\limits_{D_2}\frac{x^2}{y^2}\mathrm{d}x\mathrm{d}y\\
&=\int_{\frac 1 2}^1\frac 1 {y^2}\mathrm{d}y\int_{\frac 1 y}^2x^2\mathrm{d}x+\int_1^2\frac 1 {y^2}\mathrm{d}y\int_y^2x^2\mathrm{d}x\\
&=\frac 9 4
\end{aligned} D ∬ y 2 x 2 d x d y = D 1 ∬ y 2 x 2 d x d y + D 2 ∬ y 2 x 2 d x d y = ∫ 2 1 1 y 2 1 d y ∫ y 1 2 x 2 d x + ∫ 1 2 y 2 1 d y ∫ y 2 x 2 d x = 4 9
直角坐标系下二重积分的应用
变换累次积分的积分次序:
当原始累次积分难以求解时,可以考虑改变积分次序(即改变重积分的积分区域类型),转换为易于求解的累次积分。
例:计算 ∫ 0 1 d x ∫ x x sin y y d y \displaystyle\int_0^1\mathrm{d}x\int_x^{\sqrt x}\frac{\sin y}{y}\mathrm{d}y ∫ 0 1 d x ∫ x x y sin y d y
解:积分区域为
D : x ≤ y ≤ x , 0 ≤ x ≤ 1 D:\quad x\leq y\leq\sqrt x,\quad 0\leq x\leq 1
D : x ≤ y ≤ x , 0 ≤ x ≤ 1
∫ 0 1 d x ∫ x x sin y y d y = ∬ D sin y y d x d y = ∫ 0 1 d y ∫ y 2 y sin y y d x = ∫ 0 1 ( 1 − y ) sin y d y = 1 − sin 1 \begin{aligned}
\int_0^1\mathrm{d}x\int_x^{\sqrt x}\frac{\sin y}{y}\mathrm{d}y&=\iint\limits_D\frac{\sin y}{y}\mathrm{d}x\mathrm{d}y\\
&=\int_0^1\mathrm{d}y\int_{y^2}^y\frac{\sin y}{y}\mathrm{d}x\\
&=\int_0^1(1-y)\sin y\mathrm{d}y\\
&=1-\sin 1
\end{aligned} ∫ 0 1 d x ∫ x x y sin y d y = D ∬ y sin y d x d y = ∫ 0 1 d y ∫ y 2 y y sin y d x = ∫ 0 1 ( 1 − y ) sin y d y = 1 − sin 1
将多个累次积分合为一个二重积分:
被积函数相同的累次积分可以通过转化为一个二重积分,并改变积分次序来简化计算。
例:计算 ∫ 1 2 d x ∫ x x sin π x 2 y d y + ∫ 2 4 d x ∫ x 2 sin π x 2 y d y \displaystyle\int_1^2\mathrm{d}x\int_{\sqrt x}^x\sin\frac{\pi x}{2y}\mathrm{d}y+\int_2^4\mathrm{d}x\int_{\sqrt x}^2\sin\frac{\pi x}{2y}\mathrm{d}y ∫ 1 2 d x ∫ x x sin 2 y π x d y + ∫ 2 4 d x ∫ x 2 sin 2 y π x d y
解:令
D 1 = { ( x , y ) ∣ x ≤ y ≤ x , 1 ≤ x ≤ 2 } , D 2 = { ( x , y ) ∣ x ≤ y ≤ 2 , 2 ≤ x ≤ 4 } , D = D 1 + D 2 = { ( x , y ) ∣ y ≤ x ≤ y 2 , 1 ≤ y ≤ 2 } D_1=\{(x,y)\mid\sqrt x\leq y\leq x,1\leq x\leq 2\},\\
D_2=\{(x,y)\mid\sqrt x\leq y\leq 2,2\leq x\leq 4\},\\
D=D_1+D_2=\{(x,y)\mid y\leq x\leq y^2,1\leq y\leq 2\} D 1 = {( x , y ) ∣ x ≤ y ≤ x , 1 ≤ x ≤ 2 } , D 2 = {( x , y ) ∣ x ≤ y ≤ 2 , 2 ≤ x ≤ 4 } , D = D 1 + D 2 = {( x , y ) ∣ y ≤ x ≤ y 2 , 1 ≤ y ≤ 2 }
于是,原式可以转化为
∬ D sin π x 2 y d y = ∫ 1 2 d y ∫ y y 2 sin π x 2 y d x = ∫ 1 2 2 y π d y ∫ y y 2 sin π x 2 y d π x 2 y = ∫ 1 2 2 y π ( − cos π x 2 y ) ∣ y y 2 d y = − 2 π ∫ 1 2 y cos π y 2 d y = − 4 π 2 ∫ 1 2 y d sin π y 2 = − 4 π 2 ( y sin π y 2 ∣ 1 2 − ∫ 1 2 sin π y 2 d y ) = − 4 π 2 ( − 1 + 2 π cos π y 2 ∣ 1 2 ) = 4 π 3 ( 2 + π ) \begin{aligned}
\iint\limits_D\sin\frac{\pi x}{2y}\mathrm{d}y&=\int_1^2\mathrm{d}y\int_y^{y^2}\sin\frac{\pi x}{2y}\mathrm{d}x\\
&=\int_1^2\frac{2y}{\pi}\mathrm{d}y\int_y^{y^2}\sin\frac{\pi x}{2y}\mathrm{d}\frac{\pi x}{2y}\\
&=\int_1^2\frac{2y}{\pi}\left(-\cos\frac{\pi x}{2y}\right)\bigg|_y^{y^2}\mathrm{d}y\\
&=-\frac 2 \pi\int_1^2y\cos\frac{\pi y}{2}\mathrm{d}y\\
&=-\frac 4 {\pi^2}\int_1^2y\mathrm{d}\sin\frac{\pi y}{2}\\
&=-\frac 4 {\pi^2}\left(y\sin\frac{\pi y}{2}\bigg|_1^2-\int_1^2\sin\frac{\pi y}{2}\mathrm{d}y\right)\\
&=-\frac 4 {\pi^2}\left(-1+\frac 2 \pi\cos\frac{\pi y}{2}\bigg|_1^2\right)\\
&=\frac 4 {\pi^3}(2+\pi)
\end{aligned} D ∬ sin 2 y π x d y = ∫ 1 2 d y ∫ y y 2 sin 2 y π x d x = ∫ 1 2 π 2 y d y ∫ y y 2 sin 2 y π x d 2 y π x = ∫ 1 2 π 2 y ( − cos 2 y π x ) y y 2 d y = − π 2 ∫ 1 2 y cos 2 π y d y = − π 2 4 ∫ 1 2 y d sin 2 π y = − π 2 4 ( y sin 2 π y 1 2 − ∫ 1 2 sin 2 π y d y ) = − π 2 4 ( − 1 + π 2 cos 2 π y 1 2 ) = π 3 4 ( 2 + π )
利用对称性求解二重积分:
若积分区域 D D D y y y
若 f ( x , y ) f(x,y) f ( x , y ) x x x ∬ D f ( x , y ) d σ = 0 \displaystyle\iint\limits_D f(x,y)\mathrm{d}\sigma=0 D ∬ f ( x , y ) d σ = 0
若 f ( x , y ) f(x,y) f ( x , y ) x x x ∬ D f ( x , y ) d σ = 2 ∬ D 1 f ( x , y ) d σ \displaystyle\iint\limits_D f(x,y)\mathrm{d}\sigma=2\iint\limits_{D_1} f(x,y)\mathrm{d}\sigma D ∬ f ( x , y ) d σ = 2 D 1 ∬ f ( x , y ) d σ D 1 = D ∩ { x ≥ 0 } D_1=D\cap\{x\geq 0\} D 1 = D ∩ { x ≥ 0 }
同理,若积分区域 D D D x x x
若 f ( x , y ) f(x,y) f ( x , y ) y y y ∬ D f ( x , y ) d σ = 0 \displaystyle\iint\limits_D f(x,y)\mathrm{d}\sigma=0 D ∬ f ( x , y ) d σ = 0
若 f ( x , y ) f(x,y) f ( x , y ) y y y ∬ D f ( x , y ) d σ = 2 ∬ D 2 f ( x , y ) d σ \displaystyle\iint\limits_D f(x,y)\mathrm{d}\sigma=2\iint\limits_{D_2} f(x,y)\mathrm{d}\sigma D ∬ f ( x , y ) d σ = 2 D 2 ∬ f ( x , y ) d σ D 2 = D ∩ { y ≥ 0 } D_2=D\cap\{y\geq 0\} D 2 = D ∩ { y ≥ 0 }
二重积分的轮换对称性:
若把 x x x y y y D D D D D D y = x y=x y = x
∬ D f ( x , y ) d σ = ∬ D f ( y , x ) d σ \iint\limits_Df(x,y)\mathrm{d}\sigma=\iint\limits_Df(y,x)\mathrm{d}\sigma
D ∬ f ( x , y ) d σ = D ∬ f ( y , x ) d σ
例:设 D D D x = 0 , y = 0 , x + y = 1 x=0,y=0,x+y=1 x = 0 , y = 0 , x + y = 1 ∬ D a f ( x ) + b f ( y ) f ( x ) + f ( y ) d σ \displaystyle\iint\limits_D\frac{af(x)+bf(y)}{f(x)+f(y)}\mathrm{d}\sigma D ∬ f ( x ) + f ( y ) a f ( x ) + b f ( y ) d σ
解:设
I = ∬ D a f ( x ) + b f ( y ) f ( x ) + f ( y ) d σ = ∬ D a f ( y ) + b f ( x ) f ( x ) + f ( y ) d σ I=\iint\limits_D\frac{af(x)+bf(y)}{f(x)+f(y)}\mathrm{d}\sigma=\iint\limits_D\frac{af(y)+bf(x)}{f(x)+f(y)}\mathrm{d}\sigma
I = D ∬ f ( x ) + f ( y ) a f ( x ) + b f ( y ) d σ = D ∬ f ( x ) + f ( y ) a f ( y ) + b f ( x ) d σ
故
2 I = ∬ D a f ( x ) + b f ( y ) f ( x ) + f ( y ) d σ + ∬ D a f ( y ) + b f ( x ) f ( x ) + f ( y ) d σ = ∬ D ( a + b ) d σ = 1 2 ( a + b ) \begin{aligned}
2I&=\iint\limits_D\frac{af(x)+bf(y)}{f(x)+f(y)}\mathrm{d}\sigma+\iint\limits_D\frac{af(y)+bf(x)}{f(x)+f(y)}\mathrm{d}\sigma\\
&=\iint\limits_D(a+b)\mathrm{d}\sigma=\frac 1 2(a+b)
\end{aligned} 2 I = D ∬ f ( x ) + f ( y ) a f ( x ) + b f ( y ) d σ + D ∬ f ( x ) + f ( y ) a f ( y ) + b f ( x ) d σ = D ∬ ( a + b ) d σ = 2 1 ( a + b )
所以
∬ D a f ( x ) + b f ( y ) f ( x ) + f ( y ) d σ = 1 4 ( a + b ) \iint\limits_D\frac{af(x)+bf(y)}{f(x)+f(y)}\mathrm{d}\sigma=\frac 1 4(a+b)
D ∬ f ( x ) + f ( y ) a f ( x ) + b f ( y ) d σ = 4 1 ( a + b )
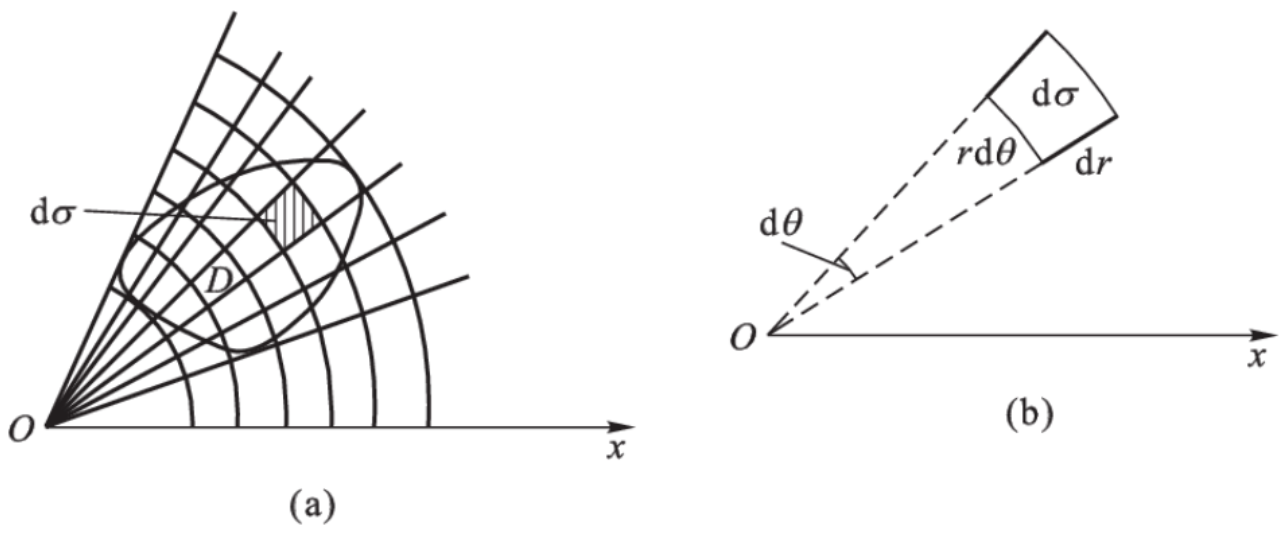
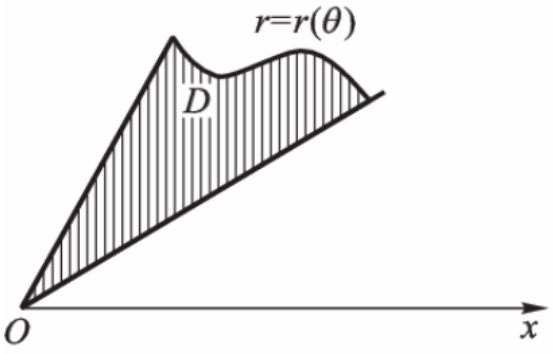
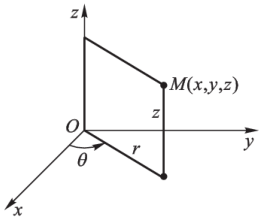
极坐标系下的二重积分
设 D D D O x y Oxy O x y
d σ = d r ⋅ ( r d θ ) = r d r d θ \mathrm{d}\sigma=\mathrm{d}r\cdot(r\mathrm{d}\theta)=r\mathrm{d}r\mathrm{d}\theta
d σ = d r ⋅ ( r d θ ) = r d r d θ
根据直角坐标与极坐标的关系,有
{ x = r cos θ y = r sin θ \begin{cases}
x=r\cos\theta\\
y=r\sin\theta
\end{cases} { x = r cos θ y = r sin θ
设 f ( x , y ) f(x,y) f ( x , y ) D D D
∬ D f ( x , y ) d σ = ∬ D f ( r cos θ , r sin θ ) r d r d θ \iint\limits_Df(x,y)\mathrm{d}\sigma=\iint\limits_Df(r\cos\theta,r\sin\theta)r\mathrm{d}r\mathrm{d}\theta
D ∬ f ( x , y ) d σ = D ∬ f ( r cos θ , r sin θ ) r d r d θ
设积分区域 D D D
D = { ( r , θ ) ∣ r 1 ( θ ) ≤ r ≤ r 2 ( θ ) , α ≤ θ ≤ β } D=\{(r,\theta)\mid r_1(\theta)\leq r\leq r_2(\theta),\alpha\leq\theta\leq\beta\}
D = {( r , θ ) ∣ r 1 ( θ ) ≤ r ≤ r 2 ( θ ) , α ≤ θ ≤ β }
其中 r 1 ( θ ) , r 2 ( θ ) r_1(\theta),r_2(\theta) r 1 ( θ ) , r 2 ( θ ) [ α , β ] [\alpha,\beta] [ α , β ]
这种区域的特点是发自极点的任意一条射线 θ = θ 0 ( θ 0 ∈ ( α , θ ) ) \theta=\theta_0\ (\theta_0\in(\alpha,\theta)) θ = θ 0 ( θ 0 ∈ ( α , θ ))
可将极坐标系下的二重积分化为先对 r r r θ \theta θ
∬ D f ( r cos θ , r sin θ ) r d r d θ = ∫ α β d θ ∫ r 1 ( θ ) r 2 ( θ ) f ( r cos θ , r sin θ ) r d r \iint\limits_Df(r\cos\theta,r\sin\theta)r\mathrm{d}r\mathrm{d}\theta=\int_\alpha^\beta\mathrm{d}\theta\int_{r_1(\theta)}^{r_2(\theta)}f(r\cos\theta,r\sin\theta)r\mathrm{d}r
D ∬ f ( r cos θ , r sin θ ) r d r d θ = ∫ α β d θ ∫ r 1 ( θ ) r 2 ( θ ) f ( r cos θ , r sin θ ) r d r
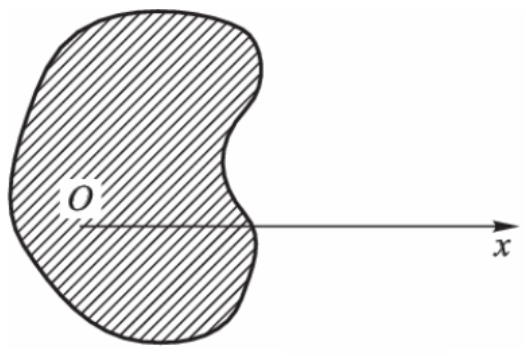
当 r 1 ( θ ) = 0 r_1(\theta)=0 r 1 ( θ ) = 0 r = r 1 ( θ ) r=r_1(\theta) r = r 1 ( θ ) O O O r 1 ( θ ) r_1(\theta) r 1 ( θ )
此时,若极点为 D D D
则累次积分可写为:
∬ D f ( r cos θ , r sin θ ) r d r d θ = ∫ 0 2 π d θ ∫ 0 r ( θ ) f ( r cos θ , r sin θ ) r d r \iint\limits_Df(r\cos\theta,r\sin\theta)r\mathrm{d}r\mathrm{d}\theta=\int_0^{2\pi}\mathrm{d}\theta\int_0^{r(\theta)}f(r\cos\theta,r\sin\theta)r\mathrm{d}r
D ∬ f ( r cos θ , r sin θ ) r d r d θ = ∫ 0 2 π d θ ∫ 0 r ( θ ) f ( r cos θ , r sin θ ) r d r
其中,r ( θ ) r(\theta) r ( θ ) D D D
极坐标系下二重积分的应用
将直角坐标转换为极坐标:
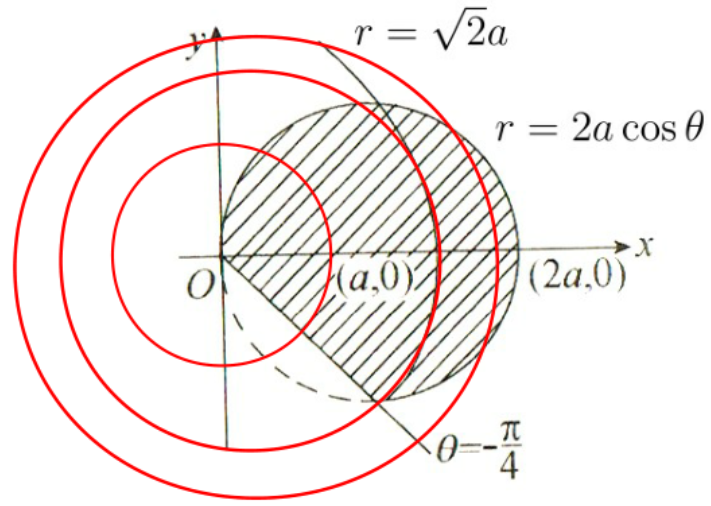
例:将直角坐标系下的二次积分化为极坐标形式下的二次积分,并计算积分值
I = ∫ 0 1 d x ∫ 1 − x 1 − x 2 ( x 2 + y 2 ) − 3 2 d y I=\int_0^1\mathrm{d}x\int_{1-x}^{\sqrt{1-x^2}}(x^2+y^2)^{-\frac 3 2}\mathrm{d}y
I = ∫ 0 1 d x ∫ 1 − x 1 − x 2 ( x 2 + y 2 ) − 2 3 d y
解:在直角坐标系中,I I I
D = { ( x , y ) ∣ 1 − x ≤ y ≤ 1 − x 2 , 0 ≤ x ≤ 1 } D=\{(x,y)\mid 1-x\leq y\leq \sqrt{1-x^2},0\leq x\leq 1\}
D = {( x , y ) ∣ 1 − x ≤ y ≤ 1 − x 2 , 0 ≤ x ≤ 1 }
用极坐标表示为
D = { ( r , θ ) ∣ 1 sin θ + cos θ ≤ r ≤ 1 , 0 ≤ θ ≤ π 2 } D=\left\{(r,\theta)\bigg|\frac 1 {\sin\theta+\cos\theta}\leq r\leq 1,0\leq\theta\leq\frac \pi 2\right\}
D = { ( r , θ ) sin θ + cos θ 1 ≤ r ≤ 1 , 0 ≤ θ ≤ 2 π }
则
I = ∬ D d x d y ( x 2 + y 2 ) 3 2 = ∫ 0 π 2 d θ ∫ 1 sin θ + cos θ 1 r d r r 3 = ∫ 0 π 2 ( − 1 r ) 1 sin θ + cos θ d θ = ∫ 0 π 2 ( sin θ + cos θ − 1 ) d θ = 2 − π 2 \begin{aligned}
I=\iint\limits_D\frac{\mathrm{d}x\mathrm{d}y}{(x^2+y^2)^{\frac 3 2}}&=\int_0^\frac\pi 2\mathrm{d}\theta\int_{\frac 1 {\sin\theta+\cos\theta}}^1\frac{r\mathrm{d}r}{r^3}\\
&=\int_0^{\frac \pi 2}\left(-\frac 1 r\right)_{\frac 1 {\sin\theta+\cos\theta}}\mathrm{d}\theta\\
&=\int_0^{\frac \pi 2}(\sin\theta+\cos\theta-1)\mathrm{d}\theta\\
&=2-\frac \pi 2
\end{aligned} I = D ∬ ( x 2 + y 2 ) 2 3 d x d y = ∫ 0 2 π d θ ∫ s i n θ + c o s θ 1 1 r 3 r d r = ∫ 0 2 π ( − r 1 ) s i n θ + c o s θ 1 d θ = ∫ 0 2 π ( sin θ + cos θ − 1 ) d θ = 2 − 2 π
变换累次积分的积分次序:
例:交换积分次序 I = ∫ − π 4 π 2 d θ ∫ 0 2 a cos θ f ( r , θ ) d r \displaystyle I=\int_{-\frac \pi 4}^{\frac \pi 2}\mathrm{d}\theta\int_0^{2a\cos\theta}f(r,\theta)\mathrm{d}r I = ∫ − 4 π 2 π d θ ∫ 0 2 a c o s θ f ( r , θ ) d r
解:
I = ∫ 0 2 a d r ∫ − π 4 arccos r 2 a f ( r , θ ) d θ + ∫ 2 a 2 a d r ∫ − arccos r 2 a arccos r 2 a f ( r , θ ) d θ I=\int_0^{\sqrt 2 a}\mathrm{d}r\int_{-\frac \pi 4}^{\arccos\frac r {2a}}f(r,\theta)\mathrm{d}\theta+\int_{\sqrt 2 a}^{2a}\mathrm{d}r\int_{-\arccos\frac r {2a}}^{\arccos\frac r {2a}}f(r,\theta)\mathrm{d}\theta
I = ∫ 0 2 a d r ∫ − 4 π a r c c o s 2 a r f ( r , θ ) d θ + ∫ 2 a 2 a d r ∫ − a r c c o s 2 a r a r c c o s 2 a r f ( r , θ ) d θ
概率积分(高斯积分):
∫ 0 + ∞ e − x 2 d x = π 2 \int_0^{+\infty}e^{-x^2}\mathrm{d}x=\frac{\sqrt\pi} 2
∫ 0 + ∞ e − x 2 d x = 2 π
解:因为 lim x → + ∞ x 2 e − x 2 = 0 \lim\limits_{x\to+\infty}x^2e^{-x^2}=0 x → + ∞ lim x 2 e − x 2 = 0
记
I ( a ) = ∬ D a e − ( x 2 + y 2 ) d x d y = ∫ 0 π 2 d θ ∫ 0 a e − r 2 r d r = π 4 ( 1 − e − a 2 ) ( a > 0 ) I(a)=\iint\limits_{D_a}e^{-(x^2+y^2)}\mathrm{d}x\mathrm{d}y=\int_0^\frac\pi 2\mathrm{d}\theta\int_0^ae^{-r^2}r\mathrm{d}r=\frac\pi 4\left(1-e^{-a^2}\right)\quad (a>0)
I ( a ) = D a ∬ e − ( x 2 + y 2 ) d x d y = ∫ 0 2 π d θ ∫ 0 a e − r 2 r d r = 4 π ( 1 − e − a 2 ) ( a > 0 )
其中
D a = { ( x , y ) ∣ x 2 + y 2 ≤ a 2 , x ≥ 0 , y ≥ 0 } K a = { ( x , y ) ∣ 0 ≤ x ≤ a , 0 ≤ y ≤ a } D_a=\{(x,y)\mid x^2+y^2\leq a^2,x\geq 0, y\geq 0\}\\
K_a=\{(x,y)\mid 0\leq x\leq a,0\leq y\leq a\} D a = {( x , y ) ∣ x 2 + y 2 ≤ a 2 , x ≥ 0 , y ≥ 0 } K a = {( x , y ) ∣ 0 ≤ x ≤ a , 0 ≤ y ≤ a }
显然有 D a ⊂ K a ⊂ D 2 a D_a\subset K_a\subset D_{\sqrt 2 a} D a ⊂ K a ⊂ D 2 a
I ( a ) < ∬ K a e − ( x 2 + y 2 ) d x d y < I ( 2 a ) I(a)<\iint\limits_{K_a}e^{-(x^2+y^2)}\mathrm{d}x\mathrm{d}y<I(\sqrt 2 a)
I ( a ) < K a ∬ e − ( x 2 + y 2 ) d x d y < I ( 2 a )
而
∬ K a e − x 2 − y 2 d x d y = ∫ 0 a e − x 2 d x ∫ 0 a e − y 2 d y = ( ∫ 0 a e − x 2 d x ) 2 \iint\limits_{K_a}e^{-x^2-y^2}\mathrm{d}x\mathrm{d}y=\int_0^ae^{-x^2}\mathrm{d}x\int_0^ae^{-y^2}\mathrm{d}y=\left(\int_0^ae^{-x^2}\mathrm{d}x\right)^2
K a ∬ e − x 2 − y 2 d x d y = ∫ 0 a e − x 2 d x ∫ 0 a e − y 2 d y = ( ∫ 0 a e − x 2 d x ) 2
因此,有
π 4 ( 1 − e − a 2 ) < ( ∫ 0 a e − x 2 d x ) 2 < π 4 ( 1 − e − 2 a 2 ) \frac\pi 4\left(1-e^{-a^2}\right)<\left(\int_0^ae^{-x^2}\mathrm{d}x\right)^2<\frac\pi 4\left(1-e^{-2a^2}\right)
4 π ( 1 − e − a 2 ) < ( ∫ 0 a e − x 2 d x ) 2 < 4 π ( 1 − e − 2 a 2 )
令 a → + ∞ a\to+\infty a → + ∞ π 4 \dfrac\pi 4 4 π
( ∫ 0 + ∞ e − x 2 d x ) 2 = π 4 \left(\int_0^{+\infty}e^{-x^2}\mathrm{d}x\right)^2=\frac\pi 4
( ∫ 0 + ∞ e − x 2 d x ) 2 = 4 π
可得概率积分的值为 π 2 \dfrac{\sqrt\pi} 2 2 π
二重积分的换元法
设 f ( x , y ) f(x,y) f ( x , y ) O x y Oxy O x y D D D
{ x = x ( u , v ) , y = y ( u , v ) , ( u , v ) ∈ D ′ \begin{cases}
x=x(u,v),\\
y=y(u,v),
\end{cases}\quad(u,v)\in D' { x = x ( u , v ) , y = y ( u , v ) , ( u , v ) ∈ D ′
其中 D ′ D' D ′ O ′ u v O'uv O ′ uv x ( u , v ) , y ( u , v ) x(u,v),y(u,v) x ( u , v ) , y ( u , v ) D ′ D' D ′ D ′ D' D ′
J = ∂ ( x , y ) ∂ ( u , v ) = ∣ ∂ x ∂ u ∂ x ∂ v ∂ y ∂ u ∂ y ∂ v ∣ ≠ 0 J=\frac{\partial(x,y)}{\partial(u,v)}=\begin{vmatrix}\dfrac{\partial x}{\partial u}&\dfrac{\partial x}{\partial v}\\\dfrac{\partial y}{\partial u}&\dfrac{\partial y}{\partial v}\end{vmatrix}\neq 0
J = ∂ ( u , v ) ∂ ( x , y ) = ∂ u ∂ x ∂ u ∂ y ∂ v ∂ x ∂ v ∂ y = 0
则有二重积分的换元公式 :
∬ D f ( x , y ) d x d y = ∬ D ′ f ( x ( u , v ) , y ( u , v ) ) ∣ J ∣ d u d v \iint\limits_D f(x,y)\mathrm{d}x\mathrm{d}y=\iint\limits_{D'}f(x(u,v),y(u,v))|J|\mathrm{d}u\mathrm{d}v
D ∬ f ( x , y ) d x d y = D ′ ∬ f ( x ( u , v ) , y ( u , v )) ∣ J ∣ d u d v
如果雅可比行列式 J J J D ′ D' D ′
例:求椭球面 x 2 a 2 + y 2 b 2 + z 2 c 2 = 1 \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}+\dfrac{z^2}{c^2}=1 a 2 x 2 + b 2 y 2 + c 2 z 2 = 1
解:设所求体积为 V V V V 1 V_1 V 1 V = 8 V 1 V=8V_1 V = 8 V 1 z = c 1 − x 2 a 2 − y 2 b 2 z=c\sqrt{1-\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}} z = c 1 − a 2 x 2 − b 2 y 2
V = 8 V 1 = 8 ∬ D c 1 − x 2 a 2 − y 2 b 2 d x d y V=8V_1=8\iint\limits_Dc\sqrt{1-\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}}\mathrm{d}x\mathrm{d}y
V = 8 V 1 = 8 D ∬ c 1 − a 2 x 2 − b 2 y 2 d x d y
积分区域 D = { ( x , y ) ∣ x 2 a 2 + y 2 b 2 ≤ 1 , x ≥ 0 , y ≥ 0 } D=\{(x,y)\mid\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}\leq 1,x\geq 0,y\geq 0\} D = {( x , y ) ∣ a 2 x 2 + b 2 y 2 ≤ 1 , x ≥ 0 , y ≥ 0 }
作如下坐标变换
{ x = a r cos θ , y = b r sin θ \begin{cases}
x=ar\cos\theta,\\
y=br\sin\theta
\end{cases} { x = a r cos θ , y = b r sin θ
在此变换下 D D D D ′ D' D ′
D ′ = { ( r , θ ) ∣ 0 ≤ r ≤ 1 , 0 ≤ θ ≤ π 2 } D'=\{(r,\theta)\mid 0\leq r\leq 1,0\leq\theta\leq\frac\pi 2\}
D ′ = {( r , θ ) ∣ 0 ≤ r ≤ 1 , 0 ≤ θ ≤ 2 π }
计算雅可比行列式
∣ J ∣ = ∣ ∂ ( x , y ) ∂ ( r , θ ) ∣ = a b r |J|=\left|\frac{\partial(x,y)}{\partial(r,\theta)}\right|=abr
∣ J ∣ = ∂ ( r , θ ) ∂ ( x , y ) = ab r
于是
V = 8 ∬ D ′ c 1 − r 2 a b r d r d θ = 8 ∫ 0 π 2 d θ ∫ 0 1 a b c 1 − r 2 r d r = 4 3 π a b c V=8\iint\limits_{D'}c\sqrt{1-r^2}abr\mathrm{d}r\mathrm{d}\theta=8\int_0^{\frac\pi 2}\mathrm{d}\theta\int_0^1abc\sqrt{1-r^2}r\mathrm{d}r=\frac 4 3 \pi abc
V = 8 D ′ ∬ c 1 − r 2 ab r d r d θ = 8 ∫ 0 2 π d θ ∫ 0 1 ab c 1 − r 2 r d r = 3 4 πab c
三重积分
将积分区域从面积拓展至体积后,我们就从二重积分拓展到了三重积分。
设 f ( x , y , z ) f(x,y,z) f ( x , y , z ) Ω ⊂ R 3 \varOmega\subset\R^3 Ω ⊂ R 3 Ω \varOmega Ω n n n
T = { Δ V 1 . Δ V 2 , ⋯ , Δ V n } T=\{\Delta V_1.\Delta V_2,\cdots,\Delta V_n\}
T = { Δ V 1 .Δ V 2 , ⋯ , Δ V n }
其中 Δ V i \Delta V_i Δ V i i i i Δ V i \Delta V_i Δ V i Δ V j \Delta V_j Δ V j ( ξ i , η i , ζ i ) ∈ Δ V i (\xi_i,\eta_i,\zeta_i)\in\Delta V_i ( ξ i , η i , ζ i ) ∈ Δ V i
∑ i = 1 n f ( ξ i , η i , ζ i ) Δ V i \sum_{i=1}^nf(\xi_i,\eta_i,\zeta_i)\Delta V_i
i = 1 ∑ n f ( ξ i , η i , ζ i ) Δ V i
以 d i d_i d i Δ V i \Delta V_i Δ V i
∣ ∣ T ∣ ∣ = max 1 ≤ i ≤ n { d i } ||T||=\max\limits_{1\leq i\leq n}\{d_i\}
∣∣ T ∣∣ = 1 ≤ i ≤ n max { d i }
如果当 ∣ ∣ T ∣ ∣ → 0 ||T||\to 0 ∣∣ T ∣∣ → 0
lim ∣ ∣ T ∣ ∣ → 0 ∑ i = 1 n f ( ξ i , η i , ζ i ) Δ V i \lim_{||T||\to 0}\sum_{i=1}^nf(\xi_i,\eta_i,\zeta_i)\Delta V_i
∣∣ T ∣∣ → 0 lim i = 1 ∑ n f ( ξ i , η i , ζ i ) Δ V i
存在,并且这个极限与区域的分割方法及点 ( ξ i , η i , ζ i ) (\xi_i,\eta_i,\zeta_i) ( ξ i , η i , ζ i ) f ( x , y , z ) f(x,y,z) f ( x , y , z ) Ω \varOmega Ω 三重积分(triple integral) ,记作
∭ Ω f ( x , y , z ) d V = lim ∣ ∣ T ∣ ∣ → 0 ∑ i = 1 n f ( ξ i , η i , ζ i ) Δ V i \iiint\limits_\varOmega f(x,y,z)\mathrm{d}V=\lim_{||T||\to 0}\sum_{i=1}^nf(\xi_i,\eta_i,\zeta_i)\Delta V_i
Ω ∭ f ( x , y , z ) d V = ∣∣ T ∣∣ → 0 lim i = 1 ∑ n f ( ξ i , η i , ζ i ) Δ V i
在直角坐标系中,体积元素 d σ = d x d y d z \mathrm{d}\sigma=\mathrm{d}x\mathrm{d}y\mathrm{d}z d σ = d x d y d z
∭ Ω f ( x , y , z ) d x d y d z \iiint\limits_\varOmega f(x,y,z)\mathrm{d}x\mathrm{d}y\mathrm{d}z
Ω ∭ f ( x , y , z ) d x d y d z
若函数 f ( x , y , z ) f(x,y,z) f ( x , y , z ) Ω \varOmega Ω Ω \varOmega Ω
三重积分有和二重积分类似的性质,并且满足
∭ Ω d V = V ( Ω ) \iiint\limits_\varOmega\mathrm{d}V=V(\varOmega)
Ω ∭ d V = V ( Ω )
三重积分的几何意义: 可以将三重积分理解为空间物体的质量,此时积分函数就能被看作是物体的密度函数。
三重积分的中值定理: 设函数 f ( x , y , z ) f(x,y,z) f ( x , y , z ) Ω \varOmega Ω V V V Ω \varOmega Ω ∃ ( ξ , η , ζ ) ∈ Ω \exists(\xi,\eta,\zeta)\in\varOmega ∃ ( ξ , η , ζ ) ∈ Ω
∭ Ω f ( x , y , z ) d V = f ( ξ , η , ζ ) V \iiint\limits_\varOmega f(x,y,z)\mathrm{d}V=f(\xi,\eta,\zeta)V
Ω ∭ f ( x , y , z ) d V = f ( ξ , η , ζ ) V
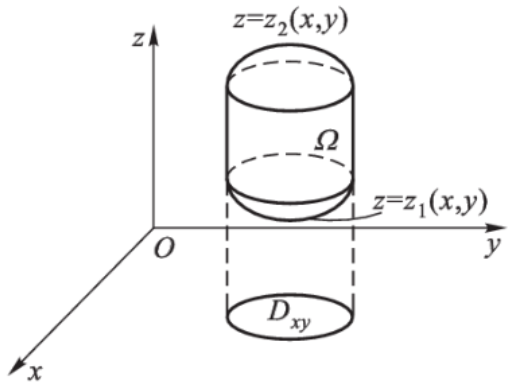
直角坐标系下的三重积分
对于积分区域 Ω \varOmega Ω
Ω = { ( x , y , z ) ∣ z 1 ( x , y ) ≤ z ≤ z 2 ( x , y ) , ( x , y ) ∈ D x y } \varOmega=\{(x,y,z)\mid z_1(x,y)\leq z\leq z_2(x,y),(x,y)\in D_{xy}\}
Ω = {( x , y , z ) ∣ z 1 ( x , y ) ≤ z ≤ z 2 ( x , y ) , ( x , y ) ∈ D x y }
则称 Ω \varOmega Ω x y \bm{xy} xy 型区域 ,其中 D x y D_{xy} D x y Ω \varOmega Ω O x y Oxy O x y z 1 ( x , y ) , z 2 ( x , y ) z_1(x,y),z_2(x,y) z 1 ( x , y ) , z 2 ( x , y ) D x y D_{xy} D x y
类似地,可以定义 x z \bm{xz} xz 型区域 和 y z \bm{yz} yz 型区域 。
法一:将三重积分化为先定积分后二重积分(投影法)
假设被积函数 f ( x , y , z ) f(x,y,z) f ( x , y , z ) x y xy x y Ω \varOmega Ω [ z 1 ( x , y ) , z 2 ( x , y ) ] [z_1(x,y),z_2(x,y)] [ z 1 ( x , y ) , z 2 ( x , y )] f ( x , y , z ) f(x,y,z) f ( x , y , z ) x , y x,y x , y F ( x , y ) F(x,y) F ( x , y )
F ( x , y ) = ∫ z 1 ( x , y ) z 2 ( x , y ) f ( x , y , z ) d z F(x,y)=\int_{z_1(x,y)}^{z_2(x,y)}f(x,y,z)\mathrm{d}z
F ( x , y ) = ∫ z 1 ( x , y ) z 2 ( x , y ) f ( x , y , z ) d z
可以证明 F ( x , y ) F(x,y) F ( x , y ) D x y D_{xy} D x y
∭ Ω f ( x , y , z ) d V = ∬ D x y F ( x , y ) d σ \iiint\limits_\varOmega f(x,y,z)\mathrm{d}V=\iint\limits_{D_{xy}}F(x,y)\mathrm{d}\sigma
Ω ∭ f ( x , y , z ) d V = D x y ∬ F ( x , y ) d σ
这样就将三重积分降为了二重积分,即
∭ Ω f ( x , y , z ) d V = ∬ D x y ( ∫ z 1 ( x , y ) z 2 ( x , y ) f ( x , y , z ) d z ) d σ \iiint\limits_\varOmega f(x,y,z)\mathrm{d}V=\iint\limits_{D_{xy}}\left(\int_{z_1(x,y)}^{z_2(x,y)}f(x,y,z)\mathrm{d}z\right)\mathrm{d}\sigma
Ω ∭ f ( x , y , z ) d V = D x y ∬ ( ∫ z 1 ( x , y ) z 2 ( x , y ) f ( x , y , z ) d z ) d σ
同理可得 x z xz x z y z yz yz
∭ Ω f ( x , y , z ) d V = ∬ D x z ( ∫ z 1 ( x , z ) z 2 ( x , z ) f ( x , y , z ) d y ) d σ ∭ Ω f ( x , y , z ) d V = ∬ D y z ( ∫ z 1 ( y , z ) z 2 ( y , z ) f ( x , y , z ) d x ) d σ \iiint\limits_\varOmega f(x,y,z)\mathrm{d}V=\iint\limits_{D_{xz}}\left(\int_{z_1(x,z)}^{z_2(x,z)}f(x,y,z)\mathrm{d}y\right)\mathrm{d}\sigma\\
\iiint\limits_\varOmega f(x,y,z)\mathrm{d}V=\iint\limits_{D_{yz}}\left(\int_{z_1(y,z)}^{z_2(y,z)}f(x,y,z)\mathrm{d}x\right)\mathrm{d}\sigma Ω ∭ f ( x , y , z ) d V = D x z ∬ ( ∫ z 1 ( x , z ) z 2 ( x , z ) f ( x , y , z ) d y ) d σ Ω ∭ f ( x , y , z ) d V = D yz ∬ ( ∫ z 1 ( y , z ) z 2 ( y , z ) f ( x , y , z ) d x ) d σ
法二:将三重积分化为累次积分
假设积分区域 Ω \varOmega Ω x y xy x y
Ω = { ( x , y , z ) ∣ z 1 ( x , y ) ≤ z ≤ z 2 ( x , y ) , ( x , y ) ∈ D } \varOmega=\{(x,y,z)\mid z_1(x,y)\leq z\leq z_2(x,y),(x,y)\in D\}
Ω = {( x , y , z ) ∣ z 1 ( x , y ) ≤ z ≤ z 2 ( x , y ) , ( x , y ) ∈ D }
当 D D D O x y Oxy O x y x x x
D = { ( x , y ) ∣ y 1 ( x ) ≤ y ≤ y 2 ( x ) , a ≤ x ≤ b } D=\{(x,y)\mid y_1(x)\leq y\leq y_2(x),a\leq x\leq b\}
D = {( x , y ) ∣ y 1 ( x ) ≤ y ≤ y 2 ( x ) , a ≤ x ≤ b }
时,有
∭ Ω f ( x , y , z ) d x d y d z = ∫ a b d x ∫ y 1 ( x ) y 2 ( x ) d y ∫ z 1 ( x , y ) z 2 ( x , y ) f ( x , y , z ) d z \iiint\limits_\varOmega f(x,y,z)\mathrm{d}x\mathrm{d}y\mathrm{d}z=\int_a^b\mathrm{d}x\int_{y_1(x)}^{y_2(x)}\mathrm{d}y\int_{z_1(x,y)}^{z_2(x,y)}f(x,y,z)\mathrm{d}z
Ω ∭ f ( x , y , z ) d x d y d z = ∫ a b d x ∫ y 1 ( x ) y 2 ( x ) d y ∫ z 1 ( x , y ) z 2 ( x , y ) f ( x , y , z ) d z
当 D D D O x y Oxy O x y y y y
D = { ( x , y ) ∣ x 1 ( x ) ≤ x ≤ x 2 ( x ) , c ≤ y ≤ d } D=\{(x,y)\mid x_1(x)\leq x\leq x_2(x),c\leq y\leq d\}
D = {( x , y ) ∣ x 1 ( x ) ≤ x ≤ x 2 ( x ) , c ≤ y ≤ d }
时,有
∭ Ω f ( x , y , z ) d x d y d z = ∫ c d d y ∫ x 1 ( y ) x 2 ( y ) d x ∫ z 1 ( x , y ) z 2 ( x , y ) f ( x , y , z ) d z \iiint\limits_\varOmega f(x,y,z)\mathrm{d}x\mathrm{d}y\mathrm{d}z=\int_c^d\mathrm{d}y\int_{x_1(y)}^{x_2(y)}\mathrm{d}x\int_{z_1(x,y)}^{z_2(x,y)}f(x,y,z)\mathrm{d}z
Ω ∭ f ( x , y , z ) d x d y d z = ∫ c d d y ∫ x 1 ( y ) x 2 ( y ) d x ∫ z 1 ( x , y ) z 2 ( x , y ) f ( x , y , z ) d z
法三:将三重积分化为先二重积分后定积分(切片法)
设 D z D_z D z O x y Oxy O x y Ω \varOmega Ω Ω \varOmega Ω
Ω = { ( x , y , z ) ∣ ( x , y ) ∈ D z , p ≤ z ≤ q } \varOmega=\{(x,y,z)\mid (x,y)\in D_z,p\leq z\leq q\}
Ω = {( x , y , z ) ∣ ( x , y ) ∈ D z , p ≤ z ≤ q }
并且当二重积分 ∬ D z f ( x , y , z ) d x d y \displaystyle\iint\limits_{D_z}f(x,y,z)\mathrm{d}x\mathrm{d}y D z ∬ f ( x , y , z ) d x d y
∭ Ω f ( x , y , z ) d x d y d z = ∫ p q d z ∬ D z f ( x , y , z ) d x d y \iiint\limits_\varOmega f(x,y,z)\mathrm{d}x\mathrm{d}y\mathrm{d}z=\int_p^q\mathrm{d}z\iint\limits_{D_z}f(x,y,z)\mathrm{d}x\mathrm{d}y
Ω ∭ f ( x , y , z ) d x d y d z = ∫ p q d z D z ∬ f ( x , y , z ) d x d y
三重积分的换元法
设 f ( x , y , z ) f(x,y,z) f ( x , y , z ) O x y z Oxyz O x yz Ω \varOmega Ω
{ x = x ( u , v , w ) , y = y ( u , v , w ) , z = z ( u , v , w ) ( u , v , w ) ∈ Ω ′ \begin{cases}
x=x(u,v,w),\\
y=y(u,v,w),\\
z=z(u,v,w)
\end{cases}\quad(u,v,w)\in \varOmega' ⎩ ⎨ ⎧ x = x ( u , v , w ) , y = y ( u , v , w ) , z = z ( u , v , w ) ( u , v , w ) ∈ Ω ′
其中 Ω ′ \varOmega' Ω ′ O ′ u v w O'uvw O ′ uv w x ( u , v , w ) , y ( u , v , w ) , z ( u , v , w ) x(u,v,w),y(u,v,w),z(u,v,w) x ( u , v , w ) , y ( u , v , w ) , z ( u , v , w ) Ω ′ \varOmega' Ω ′ Ω ′ \varOmega' Ω ′
J = ∂ ( x , y , z ) ∂ ( u , v , w ) = ∣ ∂ x ∂ u ∂ x ∂ v ∂ x ∂ w ∂ y ∂ u ∂ y ∂ v ∂ y ∂ w ∂ z ∂ u ∂ z ∂ v ∂ z ∂ w ∣ ≠ 0 J=\frac{\partial(x,y,z)}{\partial(u,v,w)}=\begin{vmatrix}\dfrac{\partial x}{\partial u}&\dfrac{\partial x}{\partial v}&\dfrac{\partial x}{\partial w}\\\dfrac{\partial y}{\partial u}&\dfrac{\partial y}{\partial v}&\dfrac{\partial y}{\partial w}\\\dfrac{\partial z}{\partial u}&\dfrac{\partial z}{\partial v}&\dfrac{\partial z}{\partial w}\end{vmatrix}\neq 0
J = ∂ ( u , v , w ) ∂ ( x , y , z ) = ∂ u ∂ x ∂ u ∂ y ∂ u ∂ z ∂ v ∂ x ∂ v ∂ y ∂ v ∂ z ∂ w ∂ x ∂ w ∂ y ∂ w ∂ z = 0
则有三重积分的换元公式 :
∭ D f ( x , y , z ) d x d y d z = ∭ D ′ f ( x ( u , v , w ) , y ( u , v , w ) , z ( u , v , w ) ) ∣ J ∣ d u d v d w \iiint\limits_D f(x,y,z)\mathrm{d}x\mathrm{d}y\mathrm{d}z=\iiint\limits_{D'}f(x(u,v,w),y(u,v,w),z(u,v,w))|J|\mathrm{d}u\mathrm{d}v\mathrm{d}w
D ∭ f ( x , y , z ) d x d y d z = D ′ ∭ f ( x ( u , v , w ) , y ( u , v , w ) , z ( u , v , w )) ∣ J ∣ d u d v d w
柱面坐标系下的三重积分
柱面坐标变换:
{ x = r cos θ , 0 ≤ r < + ∞ y = r sin θ , 0 ≤ θ ≤ 2 π z = z , − ∞ < z < + ∞ \begin{cases}
x=r\cos\theta,&0\leq r<+\infty\\
y=r\sin\theta,&0\leq\theta\leq 2\pi\\
z=z,&-\infty<z<+\infty
\end{cases} ⎩ ⎨ ⎧ x = r cos θ , y = r sin θ , z = z , 0 ≤ r < + ∞ 0 ≤ θ ≤ 2 π − ∞ < z < + ∞
直角坐标系中的点 M ( x , y , z ) M(x,y,z) M ( x , y , z ) ( r , θ , z ) (r,\theta,z) ( r , θ , z ) ( r , θ , z ) (r,\theta,z) ( r , θ , z ) M M M 柱面坐标 。
在柱面坐标变换下,雅可比行列式为
J = ∂ ( x , y , z ) ∂ ( r , θ , z ) = ∣ cos θ − r sin θ 0 sin θ r cos θ 0 0 0 1 ∣ = r J=\frac{\partial(x,y,z)}{\partial(r,\theta,z)}=\begin{vmatrix}\cos\theta&-r\sin\theta&0\\\sin\theta&r\cos\theta&0\\0&0&1\end{vmatrix}=r
J = ∂ ( r , θ , z ) ∂ ( x , y , z ) = cos θ sin θ 0 − r sin θ r cos θ 0 0 0 1 = r
若 f ( x , y , z ) f(x,y,z) f ( x , y , z ) Ω \varOmega Ω Ω ′ \varOmega' Ω ′
∭ Ω f ( x , y , z ) d x d y d z = ∭ Ω ′ f ( r cos θ , r sin θ , z ) r d r d θ d z \iiint\limits_\varOmega f(x,y,z)\mathrm dx\mathrm dy\mathrm dz=\iiint\limits_{\varOmega'}f(r\cos\theta,r\sin\theta,z)r\mathrm dr\mathrm d\theta\mathrm dz
Ω ∭ f ( x , y , z ) d x d y d z = Ω ′ ∭ f ( r cos θ , r sin θ , z ) r d r d θ d z
例:计算 ∭ Ω ( 1 + x 2 + y z ) z d V \displaystyle\iiint\limits_\varOmega\left(1+x^2+y^z\right)z\mathrm dV Ω ∭ ( 1 + x 2 + y z ) z d V Ω \varOmega Ω z = x 2 + y 2 z=\sqrt{x^2+y^2} z = x 2 + y 2 z = 1 z=1 z = 1
解:在柱面坐标系下 Ω \varOmega Ω
Ω = { ( r , θ , z ) ∣ 0 ≤ r ≤ 1 , 0 ≤ θ ≤ 2 π , r ≤ z ≤ 1 } \varOmega=\{(r,\theta,z)\mid 0\leq r\leq 1,0\leq\theta\leq 2\pi,r\leq z\leq 1\}
Ω = {( r , θ , z ) ∣ 0 ≤ r ≤ 1 , 0 ≤ θ ≤ 2 π , r ≤ z ≤ 1 }
于是
∭ Ω ( 1 + x 2 + y 2 ) z d V = ∭ Ω ( 1 + r 2 ) z r d r d θ d z = ∫ 0 2 π d θ ∫ 0 1 r ( 1 + r 2 ) d r ∫ r 1 z d z = ∫ 0 2 π d θ ∫ 0 1 1 2 r ( 1 + r 2 ) ( 1 − r 2 ) d r = 2 π ⋅ 1 2 ( 1 2 r 2 − 1 6 r 6 ) ∣ 0 1 = π 3 \begin{aligned}
\iiint\limits_\varOmega\left(1+x^2+y^2\right)z\mathrm dV&=\iiint\limits_\varOmega\left(1+r^2\right)zr\mathrm dr\mathrm d\theta\mathrm dz\\
&=\int_0^{2\pi}\mathrm d\theta\int_0^1r\left(1+r^2\right)\mathrm dr\int_r^1z\mathrm dz\\
&=\int_0^{2\pi}\mathrm d\theta\int_0^1\frac 1 2r\left(1+r^2\right)\left(1-r^2\right)\mathrm dr\\
&=2\pi\cdot\frac 1 2\left(\frac 1 2r^2-\frac 1 6r^6\right)\bigg|_0^1\\
&=\frac\pi 3
\end{aligned} Ω ∭ ( 1 + x 2 + y 2 ) z d V = Ω ∭ ( 1 + r 2 ) zr d r d θ d z = ∫ 0 2 π d θ ∫ 0 1 r ( 1 + r 2 ) d r ∫ r 1 z d z = ∫ 0 2 π d θ ∫ 0 1 2 1 r ( 1 + r 2 ) ( 1 − r 2 ) d r = 2 π ⋅ 2 1 ( 2 1 r 2 − 6 1 r 6 ) 0 1 = 3 π
球面坐标系下的三重积分
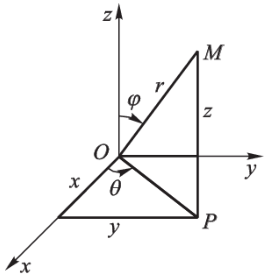
球面坐标变换:
{ x = r sin φ cos θ , 0 ≤ r < + ∞ y = r sin φ sin θ , 0 ≤ θ ≤ 2 π z = r cos φ , 0 ≤ φ ≤ π \begin{cases}
x=r\sin\varphi\cos\theta,&0\leq r<+\infty\\
y=r\sin\varphi\sin\theta,&0\leq\theta\leq 2\pi\\
z=r\cos\varphi,&0\leq\varphi\leq\pi
\end{cases} ⎩ ⎨ ⎧ x = r sin φ cos θ , y = r sin φ sin θ , z = r cos φ , 0 ≤ r < + ∞ 0 ≤ θ ≤ 2 π 0 ≤ φ ≤ π
空间中的点 M M M r , θ , φ r,\theta,\varphi r , θ , φ ( r , θ , φ ) (r,\theta,\varphi) ( r , θ , φ ) M M M 球面坐标 。
在球面坐标变换下,雅可比行列式为
J = ∂ ( x , y , z ) ∂ ( r , θ , φ ) = ∣ sin φ cos θ − r sin φ sin θ r cos φ cos θ sin φ sin θ r sin φ cos θ r cos φ sin θ cos φ 0 − r sin φ ∣ = − r 2 sin φ J=\frac{\partial(x,y,z)}{\partial(r,\theta,\varphi)}=\begin{vmatrix}\sin\varphi\cos\theta&-r\sin\varphi\sin\theta&r\cos\varphi\cos\theta\\\sin\varphi\sin\theta&r\sin\varphi\cos\theta&r\cos\varphi\sin\theta\\\cos\varphi&0&-r\sin\varphi\end{vmatrix}=-r^2\sin\varphi
J = ∂ ( r , θ , φ ) ∂ ( x , y , z ) = sin φ cos θ sin φ sin θ cos φ − r sin φ sin θ r sin φ cos θ 0 r cos φ cos θ r cos φ sin θ − r sin φ = − r 2 sin φ
若 f ( x , y , z ) f(x,y,z) f ( x , y , z ) Ω \varOmega Ω Ω ′ \varOmega' Ω ′
∭ Ω f ( x , y , z ) d x d y d z = ∭ Ω ′ F ( r , θ , φ ) r 2 sin φ d r d θ d φ \iiint\limits_\varOmega f(x,y,z)\mathrm dx\mathrm dy\mathrm dz=\iiint\limits_{\varOmega'}F(r,\theta,\varphi)r^2\sin\varphi\mathrm dr\mathrm d\theta\mathrm d\varphi
Ω ∭ f ( x , y , z ) d x d y d z = Ω ′ ∭ F ( r , θ , φ ) r 2 sin φ d r d θ d φ
其中 F ( r , θ , φ ) = f ( r sin φ cos θ , r sin φ sin θ , r cos φ ) F(r,\theta,\varphi)=f(r\sin\varphi\cos\theta,r\sin\varphi\sin\theta,r\cos\varphi) F ( r , θ , φ ) = f ( r sin φ cos θ , r sin φ sin θ , r cos φ )
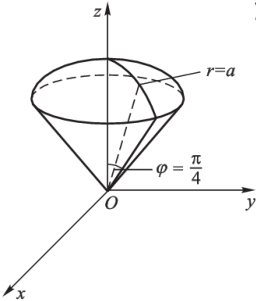
例:计算 ∭ Ω ( x 2 + x 2 + y z ) d V \displaystyle\iiint\limits_\varOmega\left(x^2+x^2+y^z\right)\mathrm dV Ω ∭ ( x 2 + x 2 + y z ) d V Ω \varOmega Ω z = x 2 + y 2 z=\sqrt{x^2+y^2} z = x 2 + y 2 z = a 2 − x 2 − y 2 z=\sqrt{a^2-x^2-y^2} z = a 2 − x 2 − y 2
解:在球面坐标系下 Ω \varOmega Ω
Ω = { ( r , θ , φ ) ∣ 0 ≤ r ≤ a , 0 ≤ θ ≤ 2 π , 0 ≤ φ ≤ π 4 } \varOmega=\{(r,\theta,\varphi)\mid 0\leq r\leq a,0\leq\theta\leq 2\pi,0\leq\varphi\leq\frac\pi 4\}
Ω = {( r , θ , φ ) ∣ 0 ≤ r ≤ a , 0 ≤ θ ≤ 2 π , 0 ≤ φ ≤ 4 π }
于是
∭ Ω ( x 2 + x 2 + y z ) d V = ∭ Ω r 2 ⋅ r 2 sin φ d r d θ d φ = ∫ 0 2 π d θ ∫ 0 π 4 sin φ d φ ∫ 0 a r 4 d r = 2 5 π a 5 ( 1 − 2 2 ) \begin{aligned}
\iiint\limits_\varOmega\left(x^2+x^2+y^z\right)\mathrm dV&=\iiint\limits_\varOmega r^2\cdot r^2\sin\varphi\mathrm dr\mathrm d\theta\mathrm d\varphi\\
&=\int_0^{2\pi}\mathrm d\theta\int_0^{\frac\pi 4}\sin\varphi\mathrm d\varphi\int_0^a r^4\mathrm dr\\
&=\frac 2 5\pi a^5\left(1-\frac{\sqrt{2}}2\right)
\end{aligned} Ω ∭ ( x 2 + x 2 + y z ) d V = Ω ∭ r 2 ⋅ r 2 sin φ d r d θ d φ = ∫ 0 2 π d θ ∫ 0 4 π sin φ d φ ∫ 0 a r 4 d r = 5 2 π a 5 ( 1 − 2 2 )
三重积分的对称性
如果 Ω \varOmega Ω O x y Oxy O x y
若 f ( x , y , z ) f(x,y,z) f ( x , y , z ) Ω \varOmega Ω z z z ∭ Ω f ( x , y , z ) d V = 0 \displaystyle\iiint\limits_\varOmega f(x,y,z)\mathrm dV=0 Ω ∭ f ( x , y , z ) d V = 0
若 f ( x , y , z ) f(x,y,z) f ( x , y , z ) Ω \varOmega Ω z z z ∭ Ω f ( x , y , z ) d V = 2 ∭ Ω 1 f ( x , y , z ) d V \displaystyle\iiint\limits_\varOmega f(x,y,z)\mathrm dV=2\iiint\limits_{\varOmega_1} f(x,y,z)\mathrm dV Ω ∭ f ( x , y , z ) d V = 2 Ω 1 ∭ f ( x , y , z ) d V Ω 1 \varOmega_1 Ω 1 Ω \varOmega Ω O x y Oxy O x y
同理可得关于 O x z , O y z Oxz,Oyz O x z , O yz
例:计算 ∭ Ω e ∣ z ∣ d V \displaystyle\iiint\limits_\varOmega e^{|z|}\mathrm dV Ω ∭ e ∣ z ∣ d V Ω \varOmega Ω x 2 + y 2 + z 2 = 1 x^2+y^2+z^2=1 x 2 + y 2 + z 2 = 1
解:设 Ω 1 \varOmega_1 Ω 1 Ω \varOmega Ω O x y Oxy O x y
D x y = { ( x , y ) ∣ x 2 + y 2 ≤ 1 − z 2 } D_{xy}=\{(x,y)\mid x^2+y^2\leq 1-z^2\}
D x y = {( x , y ) ∣ x 2 + y 2 ≤ 1 − z 2 }
则
∭ Ω e ∣ z ∣ d V = 2 ∭ Ω 1 e ∣ z ∣ d V = 2 ∫ 0 1 e z d z ∬ D x y d σ = 2 ∫ 0 1 e z π ( 1 − z 2 ) d z = 2 π ( e z ∣ 0 1 − ∫ 0 1 z 2 d e z ) = 2 π [ ( e − 1 ) − z 2 e z ∣ 0 1 + ∫ 0 1 2 z e z d z ] = 2 π [ − 1 + 2 ( z e z ∣ 0 1 − ∫ 0 1 e z d z ) ] = 2 π [ − 1 + 2 ( e − e z ∣ 0 1 ) ] = 2 π \begin{aligned}\iiint\limits_\varOmega e^{|z|}\mathrm dV&=2\iiint\limits_{\varOmega_1}e^{|z|}\mathrm dV=2\int_0^1e^z\mathrm dz\iint_{D_{xy}}\mathrm d\sigma\\
&=2\int_0^1e^z\pi\left(1-z^2\right)\mathrm dz\\
&=2\pi\left(e^z\big|_0^1-\int_0^1 z^2\mathrm de^z\right)\\
&=2\pi\left[(e-1)-z^2e^z\big|_0^1+\int_0^1 2ze^z\mathrm dz\right]\\
&=2\pi\left[-1+2\left(ze^z\big|_0^1-\int_0^1 e^z\mathrm dz\right)\right]\\
&=2\pi\left[-1+2\left(e-e^z\big|_0^1\right)\right]=2\pi
\end{aligned} Ω ∭ e ∣ z ∣ d V = 2 Ω 1 ∭ e ∣ z ∣ d V = 2 ∫ 0 1 e z d z ∬ D x y d σ = 2 ∫ 0 1 e z π ( 1 − z 2 ) d z = 2 π ( e z 0 1 − ∫ 0 1 z 2 d e z ) = 2 π [ ( e − 1 ) − z 2 e z 0 1 + ∫ 0 1 2 z e z d z ] = 2 π [ − 1 + 2 ( z e z 0 1 − ∫ 0 1 e z d z ) ] = 2 π [ − 1 + 2 ( e − e z 0 1 ) ] = 2 π
轮换对称性: 如果 Ω \varOmega Ω F ( x , y , z ) = 0 F(x,y,z)=0 F ( x , y , z ) = 0 F ( x , y , z ) = F ( y , z , x ) = F ( z , x , y ) F(x,y,z)=F(y,z,x)=F(z,x,y) F ( x , y , z ) = F ( y , z , x ) = F ( z , x , y ) Ω \varOmega Ω x , y , z x,y,z x , y , z
∭ Ω f ( x , y , z ) d V = ∭ Ω f ( y , z , x ) d V = ∭ Ω f ( z , x , y ) d V \iiint\limits_\varOmega f(x,y,z)\mathrm dV=\iiint\limits_\varOmega f(y,z,x)\mathrm dV=\iiint\limits_\varOmega f(z,x,y)\mathrm dV
Ω ∭ f ( x , y , z ) d V = Ω ∭ f ( y , z , x ) d V = Ω ∭ f ( z , x , y ) d V
例:
∭ Ω x 2 d V = 1 3 ∭ Ω ( x 2 + y 2 + z 2 ) d V = 1 3 ∫ 0 2 π d θ ∫ 0 π sin φ d φ ∫ 0 1 r 4 d r = 1 3 ⋅ 2 π ⋅ 2 ⋅ 1 5 = 4 π 15 \begin{aligned}
\iiint\limits_\varOmega x^2\mathrm dV&=\frac 1 3\iiint\limits_\varOmega\left(x^2+y^2+z^2\right)\mathrm dV\\
&=\frac 1 3\int_0^{2\pi}\mathrm d\theta\int_0^\pi\sin\varphi\mathrm d\varphi\int_0^1r^4\mathrm dr\\
&=\frac 1 3\cdot 2\pi\cdot 2\cdot\frac 1 5=\frac{4\pi}{15}
\end{aligned} Ω ∭ x 2 d V = 3 1 Ω ∭ ( x 2 + y 2 + z 2 ) d V = 3 1 ∫ 0 2 π d θ ∫ 0 π sin φ d φ ∫ 0 1 r 4 d r = 3 1 ⋅ 2 π ⋅ 2 ⋅ 5 1 = 15 4 π
含参变量的积分
积分限为常数的含参变量的积分:
记 D = { ( x , y ) ∣ a ≤ x ≤ b , c ≤ y ≤ d } D=\{(x,y)\mid a\leq x\leq b,c\leq y\leq d\} D = {( x , y ) ∣ a ≤ x ≤ b , c ≤ y ≤ d } f ( x , y ) f(x,y) f ( x , y ) D D D y ∈ [ c , d ] y\in[c,d] y ∈ [ c , d ]
I ( y ) = ∫ a b f ( x , y ) d x I(y)=\int_a^b f(x,y)\mathrm dx
I ( y ) = ∫ a b f ( x , y ) d x
确定了以 y y y I ( y ) I(y) I ( y ) 含参变量 y \bm y y 。
同理可得含参变量 x \bm x x :
I ( x ) = ∫ c d f ( x , y ) d y I(x)=\int_c^d f(x,y)\mathrm dy
I ( x ) = ∫ c d f ( x , y ) d y
定理: 若 f ( x , y ) f(x,y) f ( x , y ) D D D I ( y ) = ∫ a b f ( x , y ) d x \displaystyle I(y)=\int_a^b f(x,y)\mathrm dx I ( y ) = ∫ a b f ( x , y ) d x [ c , d ] [c,d] [ c , d ]
积分限含参变量的积分:
形如
F ( y ) = ∫ a ( y ) b ( y ) f ( x , y ) d x F(y)=\int_{a(y)}^{b(y)}f(x,y)\mathrm dx
F ( y ) = ∫ a ( y ) b ( y ) f ( x , y ) d x
的含参变量积分,其特点是不但被积函数 f ( x , y ) f(x,y) f ( x , y ) y y y
定理: 若 f ( x , y ) f(x,y) f ( x , y ) D D D a ( y ) , b ( y ) a(y),b(y) a ( y ) , b ( y ) [ c , d ] [c,d] [ c , d ] a ≤ a ( y ) ≤ b , a ≤ b ( y ) ≤ b a\leq a(y)\leq b,a\leq b(y)\leq b a ≤ a ( y ) ≤ b , a ≤ b ( y ) ≤ b F ( y ) F(y) F ( y ) [ c , d ] [c,d] [ c , d ]
曲线积分
第一类曲线积分的概念与性质
设 f ( x , y ) f(x, y) f ( x , y ) O x y Oxy O x y L L L L L L A , B A, B A , B L L L n + 1 n + 1 n + 1 A = M 0 , M 1 , ⋯ , M n = B A = M_0, M_1, \cdots, M_n = B A = M 0 , M 1 , ⋯ , M n = B L L L n n n i i i M i − 1 M i ⌢ \overset{\LARGE\frown}{M_{i - 1}M_i} M i − 1 M i ⌢ Δ s i \Delta s_i Δ s i ( ξ i , η i ) ∈ M i − 1 M i ⌢ ( i = 1 , 2 , ⋯ , n ) (\xi_i, \eta_i) \in \overset{\LARGE\frown}{M_{i - 1}M_i}\ (i = 1, 2, \cdots, n) ( ξ i , η i ) ∈ M i − 1 M i ⌢ ( i = 1 , 2 , ⋯ , n )
∑ i = 1 n f ( ξ i , η i ) Δ s i \sum_{i = 1}^n f(\xi_i, \eta_i){\Delta s_i}
i = 1 ∑ n f ( ξ i , η i ) Δ s i
记 d = max i ≤ i ≤ n { Δ s i } d = \max\limits_{i \leq i \leq n}\{ \Delta s_i \} d = i ≤ i ≤ n max { Δ s i }
lim d → 0 ∑ i = 1 n f ( ξ i , η i ) Δ s i \lim_{d \to 0} \sum_{i = 1}^n f(\xi_i, \eta_i){\Delta s_i}
d → 0 lim i = 1 ∑ n f ( ξ i , η i ) Δ s i
存在,则称此极限为函数 f ( x , y ) f(x, y) f ( x , y ) L L L 第一类曲线积分 ,记作
∫ L f ( x , y ) d s \int_L f(x, y){\mathrm ds}
∫ L f ( x , y ) d s
即
∫ L f ( x , y ) d s = lim d → 0 ∑ i = 1 n f ( ξ i , η i ) Δ s i \int_L f(x, y){\mathrm ds} = \lim_{d \to 0} \sum_{i = 1}^n f(\xi_i, \eta_i){\Delta s_i}
∫ L f ( x , y ) d s = d → 0 lim i = 1 ∑ n f ( ξ i , η i ) Δ s i
称 f ( x , y ) f(x, y) f ( x , y ) L L L d s \mathrm ds d s
若 L L L ∫ L f ( x , y ) d s \displaystyle\int_L f(x, y){\mathrm ds} ∫ L f ( x , y ) d s ∮ L f ( x , y ) d s \displaystyle\oint_L f(x, y){\mathrm ds} ∮ L f ( x , y ) d s
第一类曲线积分的性质: 和定积分的性质类似
∫ L [ k 1 f 1 ( x , y ) + k 2 f 2 ( x , y ) ] d s = k 1 ∫ L f 1 ( x , y ) d s + k 2 ∫ L f 2 ( x , y ) d s \int_L[k_1 f_1(x, y) + k_2 f_2(x, y)]\mathrm{d}s = k_1 \int_L f_1(x, y)\mathrm{d}s + k_2 \int_L f_2(x, y)\mathrm{d}s
∫ L [ k 1 f 1 ( x , y ) + k 2 f 2 ( x , y )] d s = k 1 ∫ L f 1 ( x , y ) d s + k 2 ∫ L f 2 ( x , y ) d s
对积分曲线的可加性质(L L L L 1 L_1 L 1 L 2 L_2 L 2
∫ L f ( x , y ) d s = ∫ L 1 f ( x , y ) d s + ∫ L 2 f ( x , y ) d s \int_L f(x, y)\mathrm{d}s = \int_{L_1} f(x, y)\mathrm{d}s + \int_{L_2} f(x, y)\mathrm{d}s
∫ L f ( x , y ) d s = ∫ L 1 f ( x , y ) d s + ∫ L 2 f ( x , y ) d s
当 f ( x , y ) ≡ 1 f(x, y) \equiv 1 f ( x , y ) ≡ 1 ∫ L d s \displaystyle\int_L{\mathrm ds} ∫ L d s L L L
设在 L L L f ( x , y ) ≤ g ( x , y ) f(x, y) \leq g(x, y) f ( x , y ) ≤ g ( x , y )
∫ L f ( x , y ) d s ≤ ∫ L g ( x , y ) d s \int_L f(x, y)\mathrm{d}s \leq \int_L g(x, y)\mathrm{d}s
∫ L f ( x , y ) d s ≤ ∫ L g ( x , y ) d s
∣ ∫ L f ( x , y ) d s ∣ ≤ ∫ L ∣ f ( x , y ) ∣ d s \left| \int_L f(x, y)\mathrm{d}s \right| \leq \int_L |f(x, y)|\mathrm{d}s
∫ L f ( x , y ) d s ≤ ∫ L ∣ f ( x , y ) ∣ d s
第一类曲线积分的应用: 计算旋转体侧面积:
S = ∫ L 2 π f ( x ) d s S = \int_L 2\pi f(x)\mathrm{d}s
S = ∫ L 2 π f ( x ) d s
第一类曲线积分的计算
基本方法: 将积分弧段参数化后把曲线积分化为定积分。
1. 曲线由参数方程表示: L L L { x = φ ( t ) y = ψ ( t ) ( α ≤ t ≤ β ) \begin{cases} x = \varphi(t)\\ y = \psi(t) \end{cases} (\alpha \leq t \leq \beta) { x = φ ( t ) y = ψ ( t ) ( α ≤ t ≤ β ) φ ( t ) \varphi(t) φ ( t ) ψ ( t ) \psi(t) ψ ( t ) [ α , β ] [\alpha, \beta] [ α , β ] 一阶连续导数 ,且 [ φ ′ ( t ) ] 2 + [ ψ ′ ( t ) ] 2 ≠ 0 [\varphi'(t)]^2 + [\psi'(t)]^2 \neq 0 [ φ ′ ( t ) ] 2 + [ ψ ′ ( t ) ] 2 = 0 ∫ L f ( x , y ) d s \int_L f(x, y)\mathrm{d}s ∫ L f ( x , y ) d s
∫ L f ( x , y ) d s = ∫ α β f ( φ ( t ) , ψ ( t ) ) [ φ ′ ( t ) ] 2 + [ ψ ′ ( t ) ] 2 d t \int_L f(x, y)\mathrm{d}s = \int_\alpha^\beta f(\varphi(t), \psi(t))\sqrt{[\varphi'(t)]^2 + [\psi'(t)]^2}\mathrm{d}t
∫ L f ( x , y ) d s = ∫ α β f ( φ ( t ) , ψ ( t )) [ φ ′ ( t ) ] 2 + [ ψ ′ ( t ) ] 2 d t
特殊的参数方程:当 { x = x y = ψ ( x ) ( x 0 ≤ x ≤ x 1 ) \begin{cases} x = x\\ y = \psi(x) \end{cases} (x_0 \leq x \leq x_1) { x = x y = ψ ( x ) ( x 0 ≤ x ≤ x 1 )
∫ L f ( x , y ) d s = ∫ x 0 x 1 f ( x , ψ ( x ) ) 1 + [ ψ ′ ( x ) ] 2 d x \int_L f(x, y)\mathrm{d}s = \int_{x_0}^{x_1} f(x, \psi(x))\sqrt{1 + [\psi'(x)]^2}\mathrm{d}x
∫ L f ( x , y ) d s = ∫ x 0 x 1 f ( x , ψ ( x )) 1 + [ ψ ′ ( x ) ] 2 d x
当 { x = φ ( y ) y = y ( y 0 ≤ y ≤ y 1 ) \begin{cases} x = \varphi(y)\\ y = y \end{cases} (y_0 \leq y \leq y_1) { x = φ ( y ) y = y ( y 0 ≤ y ≤ y 1 )
∫ L f ( x , y ) d s = ∫ y 0 y 1 f ( φ ( y ) , y ) [ φ ′ ( y ) ] 2 + 1 d x \int_L f(x, y)\mathrm{d}s = \int_{y_0}^{y_1} f(\varphi(y), y)\sqrt{[\varphi'(y)]^2 + 1}\mathrm{d}x
∫ L f ( x , y ) d s = ∫ y 0 y 1 f ( φ ( y ) , y ) [ φ ′ ( y ) ] 2 + 1 d x
2. 曲线由极坐标方程表示: L L L r = r ( θ ) ( α ≤ θ ≤ β ) r = r(\theta)\ (\alpha \leq \theta \leq \beta) r = r ( θ ) ( α ≤ θ ≤ β )
∫ L f ( x , y ) d s = ∫ α β f ( r ( θ ) cos θ , r ( θ ) sin θ ) [ r ( θ ) ] 2 + [ r ′ ( θ ) ] 2 d θ \int_L f(x, y)\mathrm{d}s = \int_\alpha^\beta f(r(\theta)\cos\theta, r(\theta)\sin\theta)\sqrt{[r(\theta)]^2 + [r'(\theta)]^2}\mathrm{d}\theta
∫ L f ( x , y ) d s = ∫ α β f ( r ( θ ) cos θ , r ( θ ) sin θ ) [ r ( θ ) ] 2 + [ r ′ ( θ ) ] 2 d θ
3. 空间曲线的参数方程: Γ \varGamma Γ { x = x ( t ) y = y ( t ) z = z ( t ) ( α ≤ t ≤ β ) \begin{cases} x = x(t)\\ y = y(t)\\ z = z(t) \end{cases} (\alpha \leq t \leq \beta) ⎩ ⎨ ⎧ x = x ( t ) y = y ( t ) z = z ( t ) ( α ≤ t ≤ β ) x ( t ) x(t) x ( t ) y ( t ) y(t) y ( t ) z ( t ) z(t) z ( t ) [ α , β ] [\alpha, \beta] [ α , β ] 一阶连续导数 ,且 x ′ 2 ( t ) + y ′ 2 ( t ) + z ′ 2 ( t ) ≠ 0 x'^2(t) + y'^2(t) + z'^2(t) \neq 0 x ′2 ( t ) + y ′2 ( t ) + z ′2 ( t ) = 0
∫ Γ f ( x , y , z ) d s = ∫ α β f ( x ( t ) , y ( t ) , z ( t ) ) x ′ 2 ( t ) + y ′ 2 ( t ) + z ′ 2 ( t ) d t \int_\varGamma f(x, y, z)\mathrm{d}s = \int_\alpha^\beta f(x(t), y(t), z(t))\sqrt{x'^2(t) + y'^2(t) + z'^2(t)}\mathrm{d}t
∫ Γ f ( x , y , z ) d s = ∫ α β f ( x ( t ) , y ( t ) , z ( t )) x ′2 ( t ) + y ′2 ( t ) + z ′2 ( t ) d t
利用对称性简化计算: 若平面光滑曲线 L L L y y y
∫ L f ( x , y ) d s = { 2 ∫ L ( y ≥ 0 ) f ( x , y ) d s , f ( − x , y ) = f ( x , y ) , 0 , f ( − x , y ) = − f ( x , y ) . \int_L f(x, y)\mathrm{d}s = \begin{cases}
\displaystyle 2\int_{L(y \geq 0)} f(x, y)\mathrm{d}s, & f(-x, y) = f(x, y),\\
0, & f(-x, y) = -f(x, y).
\end{cases} ∫ L f ( x , y ) d s = ⎩ ⎨ ⎧ 2 ∫ L ( y ≥ 0 ) f ( x , y ) d s , 0 , f ( − x , y ) = f ( x , y ) , f ( − x , y ) = − f ( x , y ) .
若平面光滑曲线 L L L x x x
∫ L f ( x , y ) d s = { 2 ∫ L ( x ≥ 0 ) f ( x , y ) d s , f ( x , − y ) = f ( x , y ) , 0 , f ( x , − y ) = − f ( x , y ) . \int_L f(x, y)\mathrm{d}s = \begin{cases}
\displaystyle 2\int_{L(x \geq 0)} f(x, y)\mathrm{d}s, & f(x, -y) = f(x, y),\\
0, & f(x, -y) = -f(x, y).
\end{cases} ∫ L f ( x , y ) d s = ⎩ ⎨ ⎧ 2 ∫ L ( x ≥ 0 ) f ( x , y ) d s , 0 , f ( x , − y ) = f ( x , y ) , f ( x , − y ) = − f ( x , y ) .
设空间光滑曲线 Γ \varGamma Γ { F ( x , y , z ) = 0 G ( x , y , z ) = 0 \begin{cases} F(x, y, z) = 0\\ G(x, y, z) = 0 \end{cases} { F ( x , y , z ) = 0 G ( x , y , z ) = 0
F ( x , y , z ) = F ( y , z , x ) = F ( z , x , y ) , G ( x , y , z ) = G ( y , z , x ) = G ( z , x , y ) . F(x, y, z) = F(y, z, x) = F(z, x, y),\\
G(x, y, z) = G(y, z, x) = G(z, x, y). F ( x , y , z ) = F ( y , z , x ) = F ( z , x , y ) , G ( x , y , z ) = G ( y , z , x ) = G ( z , x , y ) .
则称 Γ \varGamma Γ 轮换对称性 ,此时
∫ Γ f ( x , y , z ) d s = ∫ Γ f ( y , z , x ) d s = ∫ Γ f ( z , x , y ) d s = 1 3 ∫ Γ [ f ( x , y , z ) + f ( y , z , x ) + f ( z , x , y ) ] d s \begin{aligned}
\int_\varGamma f(x, y, z)\mathrm{d}s &= \int_\varGamma f(y, z, x)\mathrm{d}s = \int_\varGamma f(z, x, y)\mathrm{d}s\\
&= \frac{1}{3}\int_\varGamma[f(x, y, z) + f(y, z, x) + f(z, x, y)]\mathrm{d}s
\end{aligned} ∫ Γ f ( x , y , z ) d s = ∫ Γ f ( y , z , x ) d s = ∫ Γ f ( z , x , y ) d s = 3 1 ∫ Γ [ f ( x , y , z ) + f ( y , z , x ) + f ( z , x , y )] d s
第二类曲线积分的概念与性质
设 L L L O x y Oxy O x y A A A B B B P ( x , y ) , Q ( x , y ) P(x, y), Q(x, y) P ( x , y ) , Q ( x , y )
A = M 0 ( x 0 , y 0 ) , M 1 ( x 1 , y 1 ) , M 2 ( x 2 , y 2 ) , ⋯ , M n ( x n , y n ) = B A = M_0(x_0, y_0), M_1(x_1, y_1), M_2(x_2, y_2), \cdots, M_n(x_n, y_n) = B
A = M 0 ( x 0 , y 0 ) , M 1 ( x 1 , y 1 ) , M 2 ( x 2 , y 2 ) , ⋯ , M n ( x n , y n ) = B
将有向曲线 L L L n n n M i − 1 M i ⌢ ( i = 1 , 2 , ⋯ , n ) \overset{\LARGE\frown}{M_{i - 1}M_i}\ (i = 1, 2, \cdots, n) M i − 1 M i ⌢ ( i = 1 , 2 , ⋯ , n ) M i − 1 M i ⌢ \overset{\LARGE\frown}{M_{i - 1}M_i} M i − 1 M i ⌢ x x x y y y Δ x i = x i − x i − 1 \Delta x_i = x_i - x_{i - 1} Δ x i = x i − x i − 1 Δ y i = y i − y i − 1 \Delta y_i = y_i - y_{i - 1} Δ y i = y i − y i − 1 M i − 1 M i ⌢ \overset{\LARGE\frown}{M_{i - 1}M_i} M i − 1 M i ⌢ ( ξ i , η i ) (\xi_i, \eta_i) ( ξ i , η i )
∑ i = 1 n [ P ( ξ i , η i ) Δ x i + Q ( ξ i , η i ) Δ y i ] \sum_{i = 1}^n [P(\xi_i, \eta_i) \Delta x_i + Q(\xi_i, \eta_i) \Delta y_i]
i = 1 ∑ n [ P ( ξ i , η i ) Δ x i + Q ( ξ i , η i ) Δ y i ]
当各弧段长度的最大值 λ → 0 \lambda \to 0 λ → 0 L L L ( ξ i , η i ) (\xi_i, \eta_i) ( ξ i , η i )
A ( x , y ) = P ( x , y ) i + Q ( x , y ) j \bm{A}(x, y) = P(x, y)\bm{i} + Q(x, y)\bm{j}
A ( x , y ) = P ( x , y ) i + Q ( x , y ) j
在有向曲线 L L L 第二类曲线积分 ,也称为对坐标的曲线积分 ,记作
∫ L P ( x , y ) d x + Q ( x , y ) d y = lim λ → 0 ∑ i = 1 n [ P ( ξ i , η i ) Δ x i + Q ( ξ i , η i ) Δ y i ] \int_L P(x, y)\mathrm{d}x + Q(x, y)\mathrm{d}y = \lim_{\lambda \to 0}\sum_{i = 1}^n [P(\xi_i, \eta_i) \Delta x_i + Q(\xi_i, \eta_i) \Delta y_i]
∫ L P ( x , y ) d x + Q ( x , y ) d y = λ → 0 lim i = 1 ∑ n [ P ( ξ i , η i ) Δ x i + Q ( ξ i , η i ) Δ y i ]
称 P ( x , y ) , Q ( x , y ) P(x, y), Q(x, y) P ( x , y ) , Q ( x , y ) L L L
∫ L P ( x , y ) d x \displaystyle\int_L P(x, y)\mathrm{d}x ∫ L P ( x , y ) d x P ( x , y ) P(x, y) P ( x , y ) L L L x x x ∫ L Q ( x , y ) d y \displaystyle\int_L Q(x, y)\mathrm{d}y ∫ L Q ( x , y ) d y Q ( x , y ) Q(x, y) Q ( x , y ) L L L y y y
当积分曲线 L L L ∫ L P ( x , y ) d x + Q ( x , y ) d y \displaystyle\int_L P(x, y)\mathrm{d}x + Q(x, y)\mathrm{d}y ∫ L P ( x , y ) d x + Q ( x , y ) d y ∮ L P ( x , y ) d x + Q ( x , y ) d y \displaystyle\oint_L P(x, y)\mathrm{d}x + Q(x, y)\mathrm{d}y ∮ L P ( x , y ) d x + Q ( x , y ) d y
第二类曲线积分的物理意义: 质点受到变力 F ( x , y ) \bm{F}(x, y) F ( x , y ) L L L A A A B B B F ( x , y ) = P ( x , y ) i + Q ( x , y ) j \bm{F}(x, y) = P(x, y)\bm{i} + Q(x, y)\bm{j} F ( x , y ) = P ( x , y ) i + Q ( x , y ) j d r = d x i + d y j \mathrm{d}\bm{r} = \mathrm{d}x\bm{i} + \mathrm{d}y\bm{j} d r = d x i + d y j F \bm{F} F
W = ∫ L F ( x , y ) ⋅ d r = ∫ L P ( x , y ) d x + Q ( x , y ) d y W = \int_L \bm{F}(x, y) \cdot \mathrm{d}\bm{r} = \int_L P(x, y)\mathrm{d}x + Q(x, y)\mathrm{d}y
W = ∫ L F ( x , y ) ⋅ d r = ∫ L P ( x , y ) d x + Q ( x , y ) d y
第二类曲线积分的性质:
设 L L L − L -L − L L L L
∫ − L P d x + Q d y = − ∫ L P d x + Q d y \int_{-L} P\mathrm{d}x + Q\mathrm{d}y = -\int_L P\mathrm{d}x + Q\mathrm{d}y
∫ − L P d x + Q d y = − ∫ L P d x + Q d y
如果有向光滑曲线 L L L L 1 L_1 L 1 L 2 L_2 L 2
∫ L P d x + Q d y = ∫ L 1 P d x + Q d y + ∫ L 2 P d x + Q d y \int_L P\mathrm{d}x + Q\mathrm{d}y = \int_{L_1} P\mathrm{d}x + Q\mathrm{d}y + \int_{L_2} P\mathrm{d}x + Q\mathrm{d}y
∫ L P d x + Q d y = ∫ L 1 P d x + Q d y + ∫ L 2 P d x + Q d y
两类曲线积分之间的关系: 设 Γ \varGamma Γ l l l s s s Γ \varGamma Γ { x = x ( s ) y = y ( s ) z = z ( s ) ( 0 ≤ s ≤ l ) \begin{cases} x = x(s)\\ y = y(s)\\ z = z(s) \end{cases} (0 \leq s \leq l) ⎩ ⎨ ⎧ x = x ( s ) y = y ( s ) z = z ( s ) ( 0 ≤ s ≤ l ) Γ \varGamma Γ M ( x , y , z ) M(x, y, z) M ( x , y , z )
s = ( d x d s , d y d s , d z d s ) \bm{s} = \left( \frac{\mathrm{d}x}{\mathrm{d}s}, \frac{\mathrm{d}y}{\mathrm{d}s}, \frac{\mathrm{d}z}{\mathrm{d}s} \right)
s = ( d s d x , d s d y , d s d z )
于是可得曲线 Γ \varGamma Γ M M M M S MS MS
{ cos α = d x d s cos β = d y d s cos γ = d z d s \begin{cases}
\cos\alpha = \dfrac{\mathrm{d}x}{\mathrm{d}s}\\
\cos\beta = \dfrac{\mathrm{d}y}{\mathrm{d}s}\\
\cos\gamma = \dfrac{\mathrm{d}z}{\mathrm{d}s}\\
\end{cases} ⎩ ⎨ ⎧ cos α = d s d x cos β = d s d y cos γ = d s d z
可以将第二类曲线积分转化为第一类曲线积分:
∫ Γ P d x + Q d y + R d z = ∫ Γ ( P cos α + Q cos β + R cos γ ) d s \int_\varGamma P\mathrm{d}x + Q\mathrm{d}y + R\mathrm{d}z = \int_\varGamma (P\cos\alpha + Q\cos\beta + R\cos\gamma)\mathrm{d}s
∫ Γ P d x + Q d y + R d z = ∫ Γ ( P cos α + Q cos β + R cos γ ) d s
其中 P , Q , R , α , β , γ P, Q, R, \alpha, \beta, \gamma P , Q , R , α , β , γ Γ \varGamma Γ ( x , y , z ) (x, y, z) ( x , y , z )
第二类曲线积分的计算
曲线由参数方程表示: 设 P ( x , y ) P(x, y) P ( x , y ) Q ( x , y ) Q(x, y) Q ( x , y ) L L L L L L { x = φ ( t ) , y = ψ ( t ) . \begin{cases} x = \varphi(t),\\ y = \psi(t). \end{cases} { x = φ ( t ) , y = ψ ( t ) . t t t α \alpha α β \beta β M ( x , y ) M(x, y) M ( x , y ) L L L A A A B B B φ ( t ) \varphi(t) φ ( t ) ψ ( t ) \psi(t) ψ ( t ) α \alpha α β \beta β [ φ ′ ( t ) ] 2 + [ ψ ′ ( t ) ] 2 ≠ 0 [\varphi'(t)]^2 + [\psi'(t)]^2 \neq 0 [ φ ′ ( t ) ] 2 + [ ψ ′ ( t ) ] 2 = 0 ∫ L P ( x , y ) d x + Q ( x , y ) d y \int_L P(x, y)\mathrm{d}x + Q(x, y)\mathrm{d}y ∫ L P ( x , y ) d x + Q ( x , y ) d y
∫ L P ( x , y ) d x + Q ( x , y ) d y = ∫ α β [ P ( φ ( t ) , ψ ( t ) ) φ ′ ( t ) + Q ( φ ( t ) , ψ ( t ) ) ψ ′ ( t ) ] d t \int_L P(x, y)\mathrm{d}x + Q(x, y)\mathrm{d}y = \int_\alpha^\beta[P(\varphi(t), \psi(t))\varphi'(t) + Q(\varphi(t), \psi(t))\psi'(t)]\mathrm{d}t
∫ L P ( x , y ) d x + Q ( x , y ) d y = ∫ α β [ P ( φ ( t ) , ψ ( t )) φ ′ ( t ) + Q ( φ ( t ) , ψ ( t )) ψ ′ ( t )] d t
需要注意的是,此处的下限 α \alpha α L L L β \beta β L L L α \alpha α 不一定小于 β \beta β
特殊的参数方程:当 { x : a → b y = ψ ( x ) \begin{cases} x : a \to b\\ y = \psi(x) \end{cases} { x : a → b y = ψ ( x )
∫ L P ( x , y ) d x + Q ( x , y ) d y = ∫ a b [ P ( x , ψ ( x ) ) + Q ( x , ψ ( x ) ) ψ ′ ( x ) ] d x \int_L P(x, y)\mathrm{d}x + Q(x, y)\mathrm{d}y = \int_a^b[P(x, \psi(x)) + Q(x, \psi(x))\psi'(x)]\mathrm{d}x
∫ L P ( x , y ) d x + Q ( x , y ) d y = ∫ a b [ P ( x , ψ ( x )) + Q ( x , ψ ( x )) ψ ′ ( x )] d x
当 { x = φ ( y ) y : c → d \begin{cases} x = \varphi(y)\\ y : c \to d \end{cases} { x = φ ( y ) y : c → d
∫ L P ( x , y ) d x + Q ( x , y ) d y = ∫ a b [ P ( φ ( y ) , y ) φ ′ ( y ) + Q ( φ ( y ) , y ) ] d y \int_L P(x, y)\mathrm{d}x + Q(x, y)\mathrm{d}y = \int_a^b[P(\varphi(y), y)\varphi'(y) + Q(\varphi(y), y)]\mathrm{d}y
∫ L P ( x , y ) d x + Q ( x , y ) d y = ∫ a b [ P ( φ ( y ) , y ) φ ′ ( y ) + Q ( φ ( y ) , y )] d y
空间曲线的参数方程:
∫ L P ( x , y , z ) d x + Q ( x , y , z ) d y + R ( x , y , z ) d z = ∫ α β [ P ( x ( t ) , y ( t ) , z ( t ) ) x ′ ( t ) + Q ( x ( t ) , y ( t ) , z ( t ) ) y ′ ( t ) + R ( x ( t ) , y ( t ) , z ( t ) ) z ′ ( t ) ] d t \begin{aligned}
& \int_L P(x, y, z)\mathrm{d}x + Q(x, y, z)\mathrm{d}y + R(x, y, z)\mathrm{d}z\\
= & \int_\alpha^\beta[P(x(t), y(t), z(t))x'(t) + Q(x(t), y(t), z(t))y'(t)\\
&+ R(x(t), y(t), z(t))z'(t)]\mathrm{d}t
\end{aligned} = ∫ L P ( x , y , z ) d x + Q ( x , y , z ) d y + R ( x , y , z ) d z ∫ α β [ P ( x ( t ) , y ( t ) , z ( t )) x ′ ( t ) + Q ( x ( t ) , y ( t ) , z ( t )) y ′ ( t ) + R ( x ( t ) , y ( t ) , z ( t )) z ′ ( t )] d t
格林公式
格林(Green)定理: 设平面闭区域 D D D L L L P ( x , y ) P(x, y) P ( x , y ) Q ( x , y ) Q(x, y) Q ( x , y ) D D D
∬ D ( ∂ Q ∂ x − ∂ P ∂ y ) d x d y = ∮ L P d x + Q d y \iint\limits_D \left( \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} \right)\mathrm{d}x\mathrm{d}y = \oint_L P\mathrm{d}x + Q\mathrm{d}y
D ∬ ( ∂ x ∂ Q − ∂ y ∂ P ) d x d y = ∮ L P d x + Q d y
其中 L L L D D D 正向 的边界曲线,计算反向边界时需要加上负号。
对于平面区域 D D D L L L L L L D D D
特别地,在格林公式中,令 P = − y , Q = x P = -y, Q = x P = − y , Q = x
D = ∬ D d x d y = 1 2 ∮ L x d y − y d x D = \iint\limits_D \mathrm{d}x\mathrm{d}y = \frac{1}{2}\oint_L x\mathrm{d}y - y\mathrm{d}x
D = D ∬ d x d y = 2 1 ∮ L x d y − y d x
无法直接使用格林公式的情形:
修补法:将一条弧补成完整的闭合曲线。
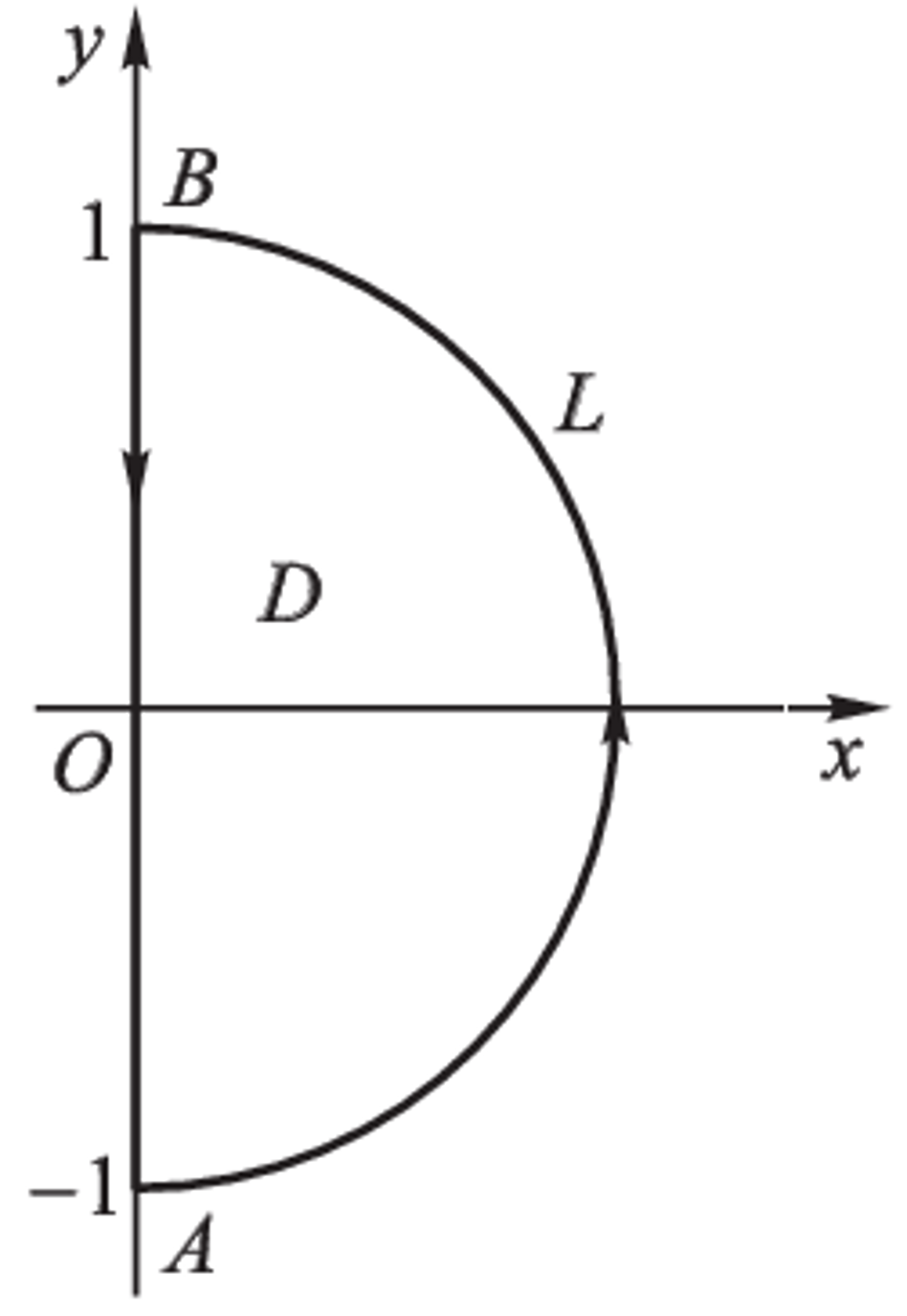
例:计算曲线积分 ∫ L ( x 2 + 1 − e y sin x ) d y − e y cos x d x \displaystyle\int_L (x^2 + 1 - e^y\sin{x})\mathrm{d}y - e^y\cos{x}\mathrm{d}x ∫ L ( x 2 + 1 − e y sin x ) d y − e y cos x d x L L L x = 1 − y 2 x = \sqrt{1 - y^2} x = 1 − y 2 A ( 0 , − 1 ) A(0, -1) A ( 0 , − 1 ) B ( 0 , 1 ) B(0, 1) B ( 0 , 1 )
解:作线段 B A BA B A C + L + B A C + L + BA C + L + B A
∫ L = ( ∫ L + ∫ B A ) − ∫ B A = ∮ C + ∫ A B \int_L = \left( \int_L + \int_{BA} \right) - \int_{BA} = \oint_C + \int_{AB}
∫ L = ( ∫ L + ∫ B A ) − ∫ B A = ∮ C + ∫ A B
令 P = − e y cos x , Q = x 2 + 1 − e y sin x P = -e^y\cos{x}, Q = x^2 + 1 - e^y\sin{x} P = − e y cos x , Q = x 2 + 1 − e y sin x
∂ Q ∂ x = 2 x − e y cos x , ∂ P ∂ y = − cos x e y \frac{\partial Q}{\partial x} = 2x - e^y\cos{x}, \quad \frac{\partial P}{\partial y} = -\cos{x}e^y
∂ x ∂ Q = 2 x − e y cos x , ∂ y ∂ P = − cos x e y
所以 ∮ C ( x 2 + 1 − e y sin x ) d y − e y cos x d x \displaystyle\oint_C (x^2 + 1 - e^y\sin{x})\mathrm{d}y - e^y\cos{x}\mathrm{d}x ∮ C ( x 2 + 1 − e y sin x ) d y − e y cos x d x
∬ D 2 x d x d y = ∫ − π 2 π 2 d θ ∫ 0 1 2 r cos θ ⋅ r d r = 4 3 \iint\limits_D 2x\mathrm{d}x\mathrm{d}y = \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\mathrm{d}\theta \int_0^1 2r\cos{\theta} \cdot r\mathrm{d}r = \frac{4}{3}
D ∬ 2 x d x d y = ∫ − 2 π 2 π d θ ∫ 0 1 2 r cos θ ⋅ r d r = 3 4
又因为
∫ A B ( x 2 + 1 − e y sin x ) d y − e y cos x d x = ∫ − 1 1 d y = 2 \int_{AB} (x^2 + 1 - e^y\sin{x})\mathrm{d}y - e^y\cos{x}\mathrm{d}x = \int_{-1}^1 \mathrm{d}y = 2
∫ A B ( x 2 + 1 − e y sin x ) d y − e y cos x d x = ∫ − 1 1 d y = 2
所以原式等于 4 3 + 2 = 10 3 \dfrac{4}{3} + 2 = \dfrac{10}{3} 3 4 + 2 = 3 10
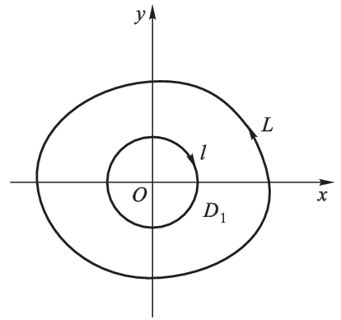
挖洞法:结合给出的条件,使挖洞后的计算尽可能简单,避免奇点带来的麻烦。
例:计算曲面积分 ∮ L x d y − y d x x 2 + y 2 \displaystyle\oint_L \frac{x\mathrm{d}y - y\mathrm{d}x}{x^2 + y^2} ∮ L x 2 + y 2 x d y − y d x L L L
解:情形 1:闭曲线 L L L D D D
令函数 P = − y x 2 + y 2 , Q = x x 2 + y 2 P = \dfrac{-y}{x^2 + y^2}, Q = \dfrac{x}{x^2 + y^2} P = x 2 + y 2 − y , Q = x 2 + y 2 x D D D
∂ P ∂ y = − x 2 + y 2 ( x 2 + y 2 ) 2 = ∂ Q ∂ x \frac{\partial P}{\partial y} = \frac{-x^2 + y^2}{(x^2 + y^2)^2} = \frac{\partial Q}{\partial x}
∂ y ∂ P = ( x 2 + y 2 ) 2 − x 2 + y 2 = ∂ x ∂ Q
所以由格林公式可得
∮ L x d y − y d x x 2 + y 2 = 0 \oint_L \frac{x\mathrm{d}y - y\mathrm{d}x}{x^2 + y^2} = 0
∮ L x 2 + y 2 x d y − y d x = 0
情形 2:闭曲线 L L L D D D
以原点为心,充分小整数 r r r l l l L L L l l l D 1 D_1 D 1 l l l
∮ L x d y − y d x x 2 + y 2 + ∮ l x d y − y d x x 2 + y 2 = 0 \oint_L \frac{x\mathrm{d}y - y\mathrm{d}x}{x^2 + y^2} + \oint_l \frac{x\mathrm{d}y - y\mathrm{d}x}{x^2 + y^2} = 0
∮ L x 2 + y 2 x d y − y d x + ∮ l x 2 + y 2 x d y − y d x = 0
所以
∮ L x d y − y d x x 2 + y 2 = − ∮ l x d y − y d x x 2 + y 2 = 1 r 2 ∮ − l x d y − y d x \oint_L \frac{x\mathrm{d}y - y\mathrm{d}x}{x^2 + y^2} = -\oint_l \frac{x\mathrm{d}y - y\mathrm{d}x}{x^2 + y^2} = \frac{1}{r^2}\oint_{-l} x\mathrm{d}y - y\mathrm{d}x
∮ L x 2 + y 2 x d y − y d x = − ∮ l x 2 + y 2 x d y − y d x = r 2 1 ∮ − l x d y − y d x
由格林公式可得
1 r 2 ∮ − l x d y − y d x = 1 r 2 ∬ D 2 d σ = 1 r 2 2 π r 2 = 2 π \frac{1}{r^2}\oint_{-l} x\mathrm{d}y - y\mathrm{d}x = \frac{1}{r^2} \iint\limits_D 2\mathrm{d}\sigma = \dfrac{1}{r^2} 2 \pi r^2 = 2\pi
r 2 1 ∮ − l x d y − y d x = r 2 1 D ∬ 2 d σ = r 2 1 2 π r 2 = 2 π
所以原式的结果为 2 π 2\pi 2 π
曲线积分基本定理
平面曲线积分与路径无关的条件:
设 L L L D D D ∫ L P d x + Q d y \displaystyle\int_L P\mathrm{d}x + Q\mathrm{d}y ∫ L P d x + Q d y L L L M 1 , M 2 M_1, M_2 M 1 , M 2 L L L M 1 M_1 M 1 M 2 M_2 M 2 L 1 , L 2 L_1, L_2 L 1 , L 2
∫ L 1 P d x + Q d y = ∫ L 2 P d x + Q d y \int_{L_1} P\mathrm{d}x + Q\mathrm{d}y = \int_{L_2} P\mathrm{d}x + Q\mathrm{d}y
∫ L 1 P d x + Q d y = ∫ L 2 P d x + Q d y
则称该曲线积分在 D D D
定理: 设 D D D 单连通域 ,如果函数 P ( x , y ) P(x, y) P ( x , y ) Q ( x , y ) Q(x, y) Q ( x , y ) D D D
沿 D D D L L L
∮ L P ( x , y ) d x + Q ( x , y ) d y = 0 \oint_L P(x, y)\mathrm{d}x + Q(x, y)\mathrm{d}y = 0
∮ L P ( x , y ) d x + Q ( x , y ) d y = 0
曲线积分 ∫ L P ( x , y ) d x + Q ( x , y ) d y \displaystyle\int_L P(x, y)\mathrm{d}x + Q(x, y)\mathrm{d}y ∫ L P ( x , y ) d x + Q ( x , y ) d y D D D
P ( x , y ) d x + Q ( x , y ) d y P(x, y)\mathrm{d}x + Q(x, y)\mathrm{d}y P ( x , y ) d x + Q ( x , y ) d y D D D u ( x , y ) u(x, y) u ( x , y ) D D D
d u ( x , y ) = P ( x , y ) d x + Q ( x , y ) d y \mathrm{d}u(x, y) = P(x, y)\mathrm{d}x + Q(x, y)\mathrm{d}y
d u ( x , y ) = P ( x , y ) d x + Q ( x , y ) d y
对于 D D D ∂ Q ∂ x = ∂ P ∂ y \dfrac{\partial Q}{\partial x} = \dfrac{\partial P}{\partial y} ∂ x ∂ Q = ∂ y ∂ P
例:若曲线积分 ∫ L x d x − a y d y x 2 + y 2 − 1 \displaystyle\int_L\frac{x\mathrm{d}x - ay\mathrm{d}y}{x^2 + y^2 - 1} ∫ L x 2 + y 2 − 1 x d x − a y d y D = { ( x , y ) ∣ x 2 + y 2 < 1 } D = \{ (x, y) \mid x^2 + y^2 < 1 \} D = {( x , y ) ∣ x 2 + y 2 < 1 } a a a
解:令 P = x x 2 + y 2 − 1 , Q = − a y x 2 + y 2 − 1 P = \dfrac{x}{x^2 + y^2 - 1}, Q = \dfrac{-ay}{x^2 + y^2 - 1} P = x 2 + y 2 − 1 x , Q = x 2 + y 2 − 1 − a y
∂ Q ∂ x = 2 a x y ( x 2 + y 2 − 1 ) 2 , ∂ P ∂ y = − 2 x y ( x 2 + y 2 − 1 ) 2 \frac{\partial Q}{\partial x} = \frac{2axy}{(x^2 + y^2 - 1)^2}, \quad \frac{\partial P}{\partial y} = \frac{-2xy}{(x^2 + y^2 - 1)^2}
∂ x ∂ Q = ( x 2 + y 2 − 1 ) 2 2 a x y , ∂ y ∂ P = ( x 2 + y 2 − 1 ) 2 − 2 x y
因为积分与路径无关,所以 ∂ Q ∂ x = ∂ P ∂ y \dfrac{\partial Q}{\partial x} = \dfrac{\partial P}{\partial y} ∂ x ∂ Q = ∂ y ∂ P
2 a x y = − 2 x y 2axy = -2xy
2 a x y = − 2 x y
所以 a = − 1 a = -1 a = − 1
梯度定理: 设 F ( x , y ) = P ( x , y ) i + Q ( x , y ) j \bm{F}(x, y) = P(x, y)\bm{i} + Q(x, y)\bm{j} F ( x , y ) = P ( x , y ) i + Q ( x , y ) j D D D P ( x , y ) P(x, y) P ( x , y ) Q ( x , y ) Q(x, y) Q ( x , y ) D D D f ( x , y ) f(x, y) f ( x , y )
F = ∇ f = ∂ f ∂ x i + ∂ f ∂ y j \bm{F} = \nabla f = \frac{\partial f}{\partial x}\bm{i} + \frac{\partial f}{\partial y}\bm{j}
F = ∇ f = ∂ x ∂ f i + ∂ y ∂ f j
则曲线积分 ∫ L F ⋅ d r \displaystyle\int_L \bm{F} \cdot \mathrm{d}\bm{r} ∫ L F ⋅ d r D D D
∫ L F ⋅ d r = f ( B ) − f ( A ) \int_L \bm{F} \cdot \mathrm{d}\bm{r} = f(B) - f(A)
∫ L F ⋅ d r = f ( B ) − f ( A )
其中 L L L D D D A A A B B B
曲面积分
第一类曲面积分
设 f ( x , y , z ) f(x, y, z) f ( x , y , z ) Σ \varSigma Σ Σ \varSigma Σ n n n Δ S 1 , Δ S 2 , ⋯ , Δ S n \Delta S_1, \Delta S_2, \cdots, \Delta S_n Δ S 1 , Δ S 2 , ⋯ , Δ S n Δ S i \Delta S_i Δ S i i i i ∀ ( ξ i , η i , ζ i ) Δ S i ( i = 1 , 2 , ⋯ , n ) \forall(\xi_i, \eta_i, \zeta_i)\Delta S_i\ (i = 1, 2, \cdots, n) ∀ ( ξ i , η i , ζ i ) Δ S i ( i = 1 , 2 , ⋯ , n )
∑ i = 1 n f ( ξ i , η i , ζ i ) Δ S i \sum_{i = 1}^n f(\xi_i, \eta_i, \zeta_i)\Delta S_i
i = 1 ∑ n f ( ξ i , η i , ζ i ) Δ S i
记 d = max i ≤ i ≤ n { d i } d = \max\limits_{i \leq i \leq n}\{ d_i \} d = i ≤ i ≤ n max { d i } d i d_i d i Δ S i \Delta S_i Δ S i
lim d → 0 ∑ i = 1 n f ( ξ i , η i , ζ i ) Δ S i \lim_{d \to 0} \sum_{i = 1}^n f(\xi_i, \eta_i, \zeta_i)\Delta S_i
d → 0 lim i = 1 ∑ n f ( ξ i , η i , ζ i ) Δ S i
存在,则称此极限为函数 f ( x , y , z ) f(x, y, z) f ( x , y , z ) Σ \varSigma Σ 第一类曲面积分 ,记作
∬ Σ f ( x , y , z ) d S \iint\limits_\varSigma f(x, y, z)\mathrm{d}S
Σ ∬ f ( x , y , z ) d S
即
∬ Σ f ( x , y , z ) d S = lim d → 0 ∑ i = 1 n f ( ξ i , η i , ζ i ) Δ S i \iint\limits_\varSigma f(x, y, z)\mathrm{d}S = \lim_{d \to 0} \sum_{i = 1}^n f(\xi_i, \eta_i, \zeta_i)\Delta S_i
Σ ∬ f ( x , y , z ) d S = d → 0 lim i = 1 ∑ n f ( ξ i , η i , ζ i ) Δ S i
称 f ( x , y , z ) f(x, y, z) f ( x , y , z ) Σ \varSigma Σ d S \mathrm{d}S d S
若 f ( x , y , z ) f(x, y, z) f ( x , y , z ) Σ \varSigma Σ ∬ Σ f ( x , y , z ) d S \displaystyle\iint_\varSigma f(x, y, z)\mathrm{d}S ∬ Σ f ( x , y , z ) d S Σ \varSigma Σ
如果 Σ \varSigma Σ 有界分片光滑闭曲面 ,即存在空间有界闭区域 Ω \varOmega Ω Σ \varSigma Σ Ω \varOmega Ω ∬ Σ f ( x , y , z ) d S \displaystyle\iint\limits_\varSigma f(x, y, z)\mathrm{d}S Σ ∬ f ( x , y , z ) d S ∯ Σ f ( x , y , z ) d S \displaystyle\oiint\limits_\varSigma f(x, y, z)\mathrm{d}S Σ ∬ f ( x , y , z ) d S
第一类曲面积分的物理意义: 物质曲面的质量可以表示为
m = ∬ Σ ρ ( x , y , z ) d S m = \iint\limits_\varSigma \rho(x, y, z)\mathrm{d}S
m = Σ ∬ ρ ( x , y , z ) d S
第一类曲面积分的计算:
若积分曲面 Σ \varSigma Σ z = z ( x , y ) z = z(x, y) z = z ( x , y ) Σ \varSigma Σ O x y Oxy O x y D x y D_{xy} D x y ( x , y ) ∈ D x y (x, y) \in D_{xy} ( x , y ) ∈ D x y z = z ( x , y ) z = z(x, y) z = z ( x , y ) D x y D_{xy} D x y f ( x , y , z ) f(x, y, z) f ( x , y , z ) Σ \varSigma Σ
∬ Σ f ( x , y , z ) d S = ∬ D x y f ( x , y , z ( x , y ) ) 1 + [ z x ′ ( x , y ) ] 2 + [ z y ′ ( x , y ) ] 2 d x d y \iint\limits_\varSigma f(x, y, z)\mathrm{d}S = \iint\limits_{D_{xy}} f(x, y, z(x, y))\sqrt{1 + [z_x'(x, y)]^2 + [z_y'(x, y)]^2}\mathrm{d}x\mathrm{d}y
Σ ∬ f ( x , y , z ) d S = D x y ∬ f ( x , y , z ( x , y )) 1 + [ z x ′ ( x , y ) ] 2 + [ z y ′ ( x , y ) ] 2 d x d y
类似地,当 Σ \varSigma Σ x = x ( y , z ) ( ( y , z ) ∈ D y z ) x = x(y, z)\ ((y, z) \in D_{yz}) x = x ( y , z ) (( y , z ) ∈ D yz ) y = y ( z , x ) ( ( z , x ) ∈ D z x ) y = y(z, x)\ ((z, x) \in D_{zx}) y = y ( z , x ) (( z , x ) ∈ D z x )
∬ Σ f ( x , y , z ) d S = ∬ D y z f ( x ( y , z ) , y , z ) 1 + [ x y ′ ( y , z ) ] 2 + [ x z ′ ( y , z ) ] 2 d y d z ∬ Σ f ( x , y , z ) d S = ∬ D x z f ( x , y ( x , z ) , z ) 1 + [ y x ′ ( x , z ) ] 2 + [ y z ′ ( x , z ) ] 2 d z d x \iint\limits_\varSigma f(x, y, z)\mathrm{d}S = \iint\limits_{D_{yz}} f(x(y, z), y, z)\sqrt{1 + [x_y'(y, z)]^2 + [x_z'(y, z)]^2}\mathrm{d}y\mathrm{d}z\\
\iint\limits_\varSigma f(x, y, z)\mathrm{d}S = \iint\limits_{D_{xz}} f(x, y(x, z), z)\sqrt{1 + [y_x'(x, z)]^2 + [y_z'(x, z)]^2}\mathrm{d}z\mathrm{d}x Σ ∬ f ( x , y , z ) d S = D yz ∬ f ( x ( y , z ) , y , z ) 1 + [ x y ′ ( y , z ) ] 2 + [ x z ′ ( y , z ) ] 2 d y d z Σ ∬ f ( x , y , z ) d S = D x z ∬ f ( x , y ( x , z ) , z ) 1 + [ y x ′ ( x , z ) ] 2 + [ y z ′ ( x , z ) ] 2 d z d x
如果积分曲面 Σ \varSigma Σ
{ x = x ( u , v ) y = y ( u , v ) z = z ( u , v ) ( u , v ) ∈ D u v \begin{cases}
x = x(u, v) \\
y = y(u, v) \\
z = z(u, v)
\end{cases} \quad (u, v) \in D_{uv} ⎩ ⎨ ⎧ x = x ( u , v ) y = y ( u , v ) z = z ( u , v ) ( u , v ) ∈ D uv
给出,其中 x ( u , v ) , y ( u , v ) , z ( u , v ) x(u, v), y(u, v), z(u, v) x ( u , v ) , y ( u , v ) , z ( u , v ) D u v D_{uv} D uv
d S = [ ∂ ( x , y ) ∂ ( u , v ) ] 2 + [ ∂ ( y , z ) ∂ ( u , v ) ] 2 + [ ∂ ( z , x ) ∂ ( u , v ) ] 2 d u d v ∬ Σ f ( x , y , z ) d S = ∬ D u v f ( x ( u , v ) , y ( u , v ) , z ( u , v ) ) ⋅ [ ∂ ( x , y ) ∂ ( u , v ) ] 2 + [ ∂ ( y , z ) ∂ ( u , v ) ] 2 + [ ∂ ( z , x ) ∂ ( u , v ) ] 2 d u d v \mathrm{d}S = \sqrt{\left[\frac{\partial(x, y)}{\partial(u, v)}\right]^2 + \left[\frac{\partial(y, z)}{\partial(u, v)}\right]^2 + \left[\frac{\partial(z, x)}{\partial(u, v)}\right]^2}\mathrm{d}u\mathrm{d}v\\
\begin{aligned}
\iint\limits_\varSigma f(x, y, z)\mathrm{d}S &= \iint\limits_{D_{uv}} f(x(u, v), y(u, v), z(u, v))\\
&\cdot \sqrt{\left[\frac{\partial(x, y)}{\partial(u, v)}\right]^2 + \left[\frac{\partial(y, z)}{\partial(u, v)}\right]^2 + \left[\frac{\partial(z, x)}{\partial(u, v)}\right]^2}\mathrm{d}u\mathrm{d}v
\end{aligned} d S = [ ∂ ( u , v ) ∂ ( x , y ) ] 2 + [ ∂ ( u , v ) ∂ ( y , z ) ] 2 + [ ∂ ( u , v ) ∂ ( z , x ) ] 2 d u d v Σ ∬ f ( x , y , z ) d S = D uv ∬ f ( x ( u , v ) , y ( u , v ) , z ( u , v )) ⋅ [ ∂ ( u , v ) ∂ ( x , y ) ] 2 + [ ∂ ( u , v ) ∂ ( y , z ) ] 2 + [ ∂ ( u , v ) ∂ ( z , x ) ] 2 d u d v
第二类曲面积分的概念与性质
曲面的侧: 设 L L L Σ \varSigma Σ M 0 M_0 M 0 Σ \varSigma Σ M M M M 0 M_0 M 0 L L L M M M L L L M 0 M_0 M 0 M M M M 0 M_0 M 0 Σ \varSigma Σ 双侧曲面 ,否则称为单侧曲面 。
取光滑曲面的法向量指向朝上的一侧为曲面的上侧 ,反之为曲面的下侧 ;取闭曲面的法向量指向朝外的一侧为曲面的外侧 ,反之为曲面的内侧 。
设函数 P ( x , y , z ) , Q ( x , y , z ) , R ( x , y , z ) P(x, y, z), Q(x, y, z), R(x, y, z) P ( x , y , z ) , Q ( x , y , z ) , R ( x , y , z ) Σ \varSigma Σ Σ \varSigma Σ n n n Δ Σ i \Delta\varSigma_i Δ Σ i Δ S i \Delta S_i Δ S i Δ Σ i \Delta\varSigma_i Δ Σ i O y z Oyz O yz O z x Ozx O z x O x y Oxy O x y ( Δ y Δ z ) i (\Delta y \Delta z)_i ( Δ y Δ z ) i ( Δ y Δ z ) i (\Delta y \Delta z)_i ( Δ y Δ z ) i ( Δ x Δ y ) i (\Delta x \Delta y)_i ( Δ x Δ y ) i Δ Σ i \Delta\varSigma_i Δ Σ i ( ξ i , η i , ζ i ) (\xi_i, \eta_i, \zeta_i) ( ξ i , η i , ζ i )
∑ i = 1 n [ P ( ξ i , η i , ζ i ) ( Δ y Δ z ) i + Q ( ξ i , η i , ζ i ) ( Δ z Δ x ) i + R ( ξ i , η i , ζ i ) ( Δ x Δ y ) i ] \sum_{i = 1}^n[P(\xi_i, \eta_i, \zeta_i)(\Delta y \Delta z)_i + Q(\xi_i, \eta_i, \zeta_i)(\Delta z \Delta x)_i + R(\xi_i, \eta_i, \zeta_i)(\Delta x \Delta y)_i]
i = 1 ∑ n [ P ( ξ i , η i , ζ i ) ( Δ y Δ z ) i + Q ( ξ i , η i , ζ i ) ( Δ z Δ x ) i + R ( ξ i , η i , ζ i ) ( Δ x Δ y ) i ]
若当各小片曲面的直径的最大值 λ → 0 \lambda \to 0 λ → 0 Σ \varSigma Σ ( ξ i , η i , ζ i ) (\xi_i, \eta_i, \zeta_i) ( ξ i , η i , ζ i )
A ( x , y , z ) = P ( x , y , z ) i + Q ( x , y , z ) j + R ( x , y , z ) k \bm{A}(x, y, z) = P(x, y, z)\bm{i} + Q(x, y, z)\bm{j} + R(x, y, z)\bm{k}
A ( x , y , z ) = P ( x , y , z ) i + Q ( x , y , z ) j + R ( x , y , z ) k
在有向曲面 Σ \varSigma Σ 第二类曲面积分 ,也称为对坐标的曲面积分 ,记作
∬ Σ P ( x , y , z ) d y d z + Q ( x , y , z ) d z d x + R ( x , y , z ) d x d y = lim λ → 0 ∑ i = 1 n [ P ( ξ i , η i , ζ i ) ( Δ y Δ z ) i + Q ( ξ i , η i , ζ i ) ( Δ z Δ x ) i + R ( ξ i , η i , ζ i ) ( Δ x Δ y ) i ] \begin{aligned}
& \iint\limits_\varSigma P(x, y, z)\mathrm{d}y\mathrm{d}z + Q(x, y, z)\mathrm{d}z\mathrm{d}x + R(x, y, z)\mathrm{d}x\mathrm{d}y\\
= & \lim_{\lambda \to 0} \sum_{i = 1}^n[P(\xi_i, \eta_i, \zeta_i)(\Delta y \Delta z)_i + Q(\xi_i, \eta_i, \zeta_i)(\Delta z \Delta x)_i + R(\xi_i, \eta_i, \zeta_i)(\Delta x \Delta y)_i]
\end{aligned} = Σ ∬ P ( x , y , z ) d y d z + Q ( x , y , z ) d z d x + R ( x , y , z ) d x d y λ → 0 lim i = 1 ∑ n [ P ( ξ i , η i , ζ i ) ( Δ y Δ z ) i + Q ( ξ i , η i , ζ i ) ( Δ z Δ x ) i + R ( ξ i , η i , ζ i ) ( Δ x Δ y ) i ]
称 P ( x , y , z ) , Q ( x , y , z ) , R ( x , y , z ) P(x, y, z), Q(x, y, z), R(x, y, z) P ( x , y , z ) , Q ( x , y , z ) , R ( x , y , z ) Σ \varSigma Σ
函数 P ( x , y , z ) , Q ( x , y , z ) , R ( x , y , z ) P(x, y, z), Q(x, y, z), R(x, y, z) P ( x , y , z ) , Q ( x , y , z ) , R ( x , y , z ) Σ \varSigma Σ y , z y, z y , z z , x z, x z , x x , y x, y x , y
∬ Σ P ( x , y , z ) d y d z , ∬ Σ Q ( x , y , z ) d z d x , ∬ Σ R ( x , y , z ) d x d y \iint\limits_\varSigma P(x, y, z)\mathrm{d}y\mathrm{d}z, \quad \iint\limits_\varSigma Q(x, y, z)\mathrm{d}z\mathrm{d}x, \quad \iint\limits_\varSigma R(x, y, z)\mathrm{d}x\mathrm{d}y
Σ ∬ P ( x , y , z ) d y d z , Σ ∬ Q ( x , y , z ) d z d x , Σ ∬ R ( x , y , z ) d x d y
如果 Σ \varSigma Σ
∯ Σ P ( x , y , z ) d y d z + Q ( x , y , z ) d z d x + R ( x , y , z ) d x d y \oiint\limits_\varSigma P(x, y, z)\mathrm{d}y\mathrm{d}z + Q(x, y, z)\mathrm{d}z\mathrm{d}x + R(x, y, z)\mathrm{d}x\mathrm{d}y
Σ ∬ P ( x , y , z ) d y d z + Q ( x , y , z ) d z d x + R ( x , y , z ) d x d y
第二类曲面积分的性质:
积分曲面的可加性:设 Σ \varSigma Σ Σ 1 \varSigma_1 Σ 1 Σ 2 \varSigma_2 Σ 2
∬ Σ P d y d z + Q d z d x + R d x d y = ∬ Σ 1 P d y d z + Q d z d x + R d x d y + ∬ Σ 2 P d y d z + Q d z d x + R d x d y \begin{aligned}
& \iint\limits_\varSigma P\mathrm{d}y\mathrm{d}z + Q\mathrm{d}z\mathrm{d}x + R\mathrm{d}x\mathrm{d}y\\
= & \iint\limits_{\varSigma_1} P\mathrm{d}y\mathrm{d}z + Q\mathrm{d}z\mathrm{d}x + R\mathrm{d}x\mathrm{d}y + \iint\limits_{\varSigma_2} P\mathrm{d}y\mathrm{d}z + Q\mathrm{d}z\mathrm{d}x + R\mathrm{d}x\mathrm{d}y
\end{aligned} = Σ ∬ P d y d z + Q d z d x + R d x d y Σ 1 ∬ P d y d z + Q d z d x + R d x d y + Σ 2 ∬ P d y d z + Q d z d x + R d x d y
设 − Σ -\varSigma − Σ Σ \varSigma Σ
∬ Σ P d y d z + Q d z d x + R d x d y = − ∬ − Σ P d y d z + Q d z d x + R d x d y \iint\limits_\varSigma P\mathrm{d}y\mathrm{d}z + Q\mathrm{d}z\mathrm{d}x + R\mathrm{d}x\mathrm{d}y = -\iint\limits_{-\varSigma} P\mathrm{d}y\mathrm{d}z + Q\mathrm{d}z\mathrm{d}x + R\mathrm{d}x\mathrm{d}y
Σ ∬ P d y d z + Q d z d x + R d x d y = − − Σ ∬ P d y d z + Q d z d x + R d x d y
两类曲面积分之间的关系: 设 cos α , cos β , cos γ \cos\alpha, \cos\beta, \cos\gamma cos α , cos β , cos γ Σ \varSigma Σ M ( x , y , z ) M(x, y, z) M ( x , y , z )
∬ Σ P d y d z + Q d z d x + R d x d y = ∬ Σ ( P cos α + Q cos β + R cos γ ) d S \iint\limits_\varSigma P\mathrm{d}y\mathrm{d}z + Q\mathrm{d}z\mathrm{d}x + R\mathrm{d}x\mathrm{d}y = \iint\limits_\varSigma (P\cos\alpha + Q\cos\beta + R\cos\gamma)\mathrm{d}S
Σ ∬ P d y d z + Q d z d x + R d x d y = Σ ∬ ( P cos α + Q cos β + R cos γ ) d S
第二类曲面积分的计算
分面投影法:
设函数 R ( x , y , z ) R(x, y, z) R ( x , y , z ) Σ \varSigma Σ z = z ( x , y ) , ( x , y ) ∈ D x y z = z(x, y),\ (x, y) \in D_{xy} z = z ( x , y ) , ( x , y ) ∈ D x y D x y D_{xy} D x y Σ \varSigma Σ O x y Oxy O x y
∬ Σ R ( x , y , z ) d x d y = ± ∬ D x y R ( x , y , z ( x , y ) ) d x d y \iint\limits_\varSigma R(x, y, z)\mathrm{d}x\mathrm{d}y = \pm\iint\limits_{D_{xy}} R(x, y, z(x, y))\mathrm{d}x\mathrm{d}y
Σ ∬ R ( x , y , z ) d x d y = ± D x y ∬ R ( x , y , z ( x , y )) d x d y
其中当 Σ \varSigma Σ cos γ > 0 \cos\gamma > 0 cos γ > 0 Σ \varSigma Σ cos γ < 0 \cos\gamma < 0 cos γ < 0
类似地,当 Σ \varSigma Σ x = x ( y , z ) ( ( y , z ) ∈ D y z ) x = x(y, z)\ ((y, z) \in D_{yz}) x = x ( y , z ) (( y , z ) ∈ D yz ) y = y ( z , x ) ( ( z , x ) ∈ D z x ) y = y(z, x)\ ((z, x) \in D_{zx}) y = y ( z , x ) (( z , x ) ∈ D z x ) D y z D_{yz} D yz D z x D_{zx} D z x Σ \varSigma Σ O y z Oyz O yz O z x Ozx O z x
∬ Σ P ( x , y , z ) d y d z = ± ∬ D y z P ( x ( y , z ) , y , z ) d y d z ∬ Σ Q ( x , y , z ) d z d x = ± ∬ D z x Q ( x , y ( z , x ) , ) d z d x \iint\limits_\varSigma P(x, y, z)\mathrm{d}y\mathrm{d}z = \pm\iint\limits_{D_{yz}} P(x(y, z), y, z)\mathrm{d}y\mathrm{d}z\\
\iint\limits_\varSigma Q(x, y, z)\mathrm{d}z\mathrm{d}x = \pm\iint\limits_{D_{zx}} Q(x, y(z, x), )\mathrm{d}z\mathrm{d}x Σ ∬ P ( x , y , z ) d y d z = ± D yz ∬ P ( x ( y , z ) , y , z ) d y d z Σ ∬ Q ( x , y , z ) d z d x = ± D z x ∬ Q ( x , y ( z , x ) , ) d z d x
第二类曲面积分为 0 的三种特殊情况:
当曲面 Σ \varSigma Σ O x y Oxy O x y ∬ Σ R ( x , y , z ) d x d y = 0 \displaystyle\iint\limits_\varSigma R(x, y, z)\mathrm{d}x\mathrm{d}y = 0 Σ ∬ R ( x , y , z ) d x d y = 0
当曲面 Σ \varSigma Σ O y z Oyz O yz ∬ Σ P ( x , y , z ) d y d z = 0 \displaystyle\iint\limits_\varSigma P(x, y, z)\mathrm{d}y\mathrm{d}z = 0 Σ ∬ P ( x , y , z ) d y d z = 0
当曲面 Σ \varSigma Σ O z x Ozx O z x ∬ Σ Q ( x , y , z ) d z d x = 0 \displaystyle\iint\limits_\varSigma Q(x, y, z)\mathrm{d}z\mathrm{d}x = 0 Σ ∬ Q ( x , y , z ) d z d x = 0
合一投影法:
如果 Σ \varSigma Σ z = z ( x , y ) , ( x , y ) ∈ D x y z = z(x, y),\ (x, y) \in D_{xy} z = z ( x , y ) , ( x , y ) ∈ D x y D x y D_{xy} D x y Σ \varSigma Σ O x y Oxy O x y P , Q , R P, Q, R P , Q , R Σ \varSigma Σ
∬ Σ P ( x , y , z ) d y d z + Q ( x , y , z ) d z d x + R ( x , y , z ) d x d y = ± ∬ D x y { P [ x , y , z ( x , y ) ] [ − z x ( x , y ) ] + Q [ x , y , z ( x , y ) ] [ − z y ( x , y ) ] + R [ x , y , z ( x , y ) ] ⋅ 1 } d x d y \begin{aligned}
& \iint\limits_\varSigma P(x, y, z)\mathrm{d}y\mathrm{d}z + Q(x, y, z)\mathrm{d}z\mathrm{d}x + R(x, y, z)\mathrm{d}x\mathrm{d}y\\
= & \pm\iint\limits_{D_{xy}} \{ P[x, y, z(x, y)][-z_x(x, y)] + Q[x, y, z(x, y)][-z_y(x, y)]\\
&+ R[x, y, z(x, y)] \cdot 1 \}\mathrm{d}x\mathrm{d}y
\end{aligned} = Σ ∬ P ( x , y , z ) d y d z + Q ( x , y , z ) d z d x + R ( x , y , z ) d x d y ± D x y ∬ { P [ x , y , z ( x , y )] [ − z x ( x , y )] + Q [ x , y , z ( x , y )] [ − z y ( x , y )] + R [ x , y , z ( x , y )] ⋅ 1 } d x d y
当 Σ \varSigma Σ Σ \varSigma Σ
高斯公式与散度
高斯(Gauss)公式: 设空间闭区域 Ω \varOmega Ω Σ \varSigma Σ P ( x , y , z ) , Q ( x , y , z ) , R ( x , y , z ) P(x, y, z), Q(x, y, z), R(x, y, z) P ( x , y , z ) , Q ( x , y , z ) , R ( x , y , z ) Ω \varOmega Ω
∭ Ω ( ∂ P ∂ x + ∂ Q ∂ y + ∂ R ∂ z ) d V = ∯ Σ P d y d z + Q d z d x + R d x d y \iiint\limits_\varOmega \left( \frac{\partial P}{\partial x} + \frac{\partial Q}{\partial y} + \frac{\partial R}{\partial z} \right)\mathrm{d}V = \oiint\limits_\varSigma P\mathrm{d}y\mathrm{d}z + Q\mathrm{d}z\mathrm{d}x + R\mathrm{d}x\mathrm{d}y
Ω ∭ ( ∂ x ∂ P + ∂ y ∂ Q + ∂ z ∂ R ) d V = Σ ∬ P d y d z + Q d z d x + R d x d y
或
∭ Ω ( ∂ P ∂ x + ∂ Q ∂ y + ∂ R ∂ z ) d V = ∯ Σ ( P cos α + Q cos β + R cos γ ) d S \iiint\limits_\varOmega \left( \frac{\partial P}{\partial x} + \frac{\partial Q}{\partial y} + \frac{\partial R}{\partial z} \right)\mathrm{d}V = \oiint\limits_\varSigma (P\cos\alpha + Q\cos\beta + R\cos\gamma)\mathrm{d}S
Ω ∭ ( ∂ x ∂ P + ∂ y ∂ Q + ∂ z ∂ R ) d V = Σ ∬ ( P cos α + Q cos β + R cos γ ) d S
其中 Σ \varSigma Σ Ω \varOmega Ω 外侧 ,cos α , cos β , cos γ \cos\alpha, \cos\beta, \cos\gamma cos α , cos β , cos γ Σ \varSigma Σ ( x , y , z ) (x, y, z) ( x , y , z )
散度(divergence): 设向量场
A ( x , y , z ) = P ( x , y , z ) i + Q ( x , y , z ) j + R ( x , y , z ) k \bm{A}(x, y, z) = \bm{P}(x, y, z)\bm{i} + \bm{Q}(x, y, z)\bm{j} + \bm{R}(x, y, z)\bm{k}
A ( x , y , z ) = P ( x , y , z ) i + Q ( x , y , z ) j + R ( x , y , z ) k
其中函数 P , Q , R P, Q, R P , Q , R Σ \varSigma Σ n \bm{n} n ∑ \sum ∑ ( x , y , z ) (x, y, z) ( x , y , z )
∬ Σ A ⋅ n d S \iint\limits_\varSigma \bm{A} \cdot \bm{n}\mathrm{d}S
Σ ∬ A ⋅ n d S
称为向量场 A \bm{A} A Σ \varSigma Σ 通量(flux) 。向量场 A \bm{A} A
∂ P ∂ x + ∂ Q ∂ y + ∂ R ∂ z \frac{\partial P}{\partial x} + \frac{\partial Q}{\partial y} + \frac{\partial R}{\partial z}
∂ x ∂ P + ∂ y ∂ Q + ∂ z ∂ R
记作 d i v A \mathrm{div}\bm{A} div A ∇ = ( ∂ ∂ x + ∂ ∂ y + ∂ ∂ z ) \nabla = (\dfrac{\partial}{\partial x} + \dfrac{\partial}{\partial y} + \dfrac{\partial}{\partial z}) ∇ = ( ∂ x ∂ + ∂ y ∂ + ∂ z ∂ ) A \bm{A} A
d i v A = ∇ ⋅ A \mathrm{div}\bm{A} = \nabla\cdot\bm{A}
div A = ∇ ⋅ A
高斯公式可以用散度来定义:
∯ Σ A ⋅ d S = ∭ Ω d i v A d V \oiint\limits_\varSigma \bm{A} \cdot \mathrm{d}\bm{S} = \iiint\limits_\varOmega \mathrm{div}\bm{A}\mathrm{d}V
Σ ∬ A ⋅ d S = Ω ∭ div A d V
斯托克斯公式与旋度
斯托克斯公式可以用于转换第二类曲线积分和第二类曲面积分。
斯托克斯(Stokes)公式: 设 Γ \varGamma Γ Σ \varSigma Σ Γ \varGamma Γ Γ \varGamma Γ Σ \varSigma Σ P ( x , y , z ) , Q ( x , y , z ) , R ( x , y , z ) P(x, y, z), Q(x, y, z), R(x, y, z) P ( x , y , z ) , Q ( x , y , z ) , R ( x , y , z ) Σ \varSigma Σ Γ \varGamma Γ
∮ Γ P d x + Q d y + R d z = ∬ Σ ( ∂ R ∂ y − ∂ Q ∂ z ) d y d z + ( ∂ P ∂ z − ∂ R ∂ x ) d z d x + ( ∂ Q ∂ x − ∂ P ∂ y ) d x d y \begin{aligned}
& \oint_\varGamma P\mathrm{d}x + Q\mathrm{d}y + R\mathrm{d}z\\
= & \iint\limits_\varSigma \left( \frac{\partial R}{\partial y} - \frac{\partial Q}{\partial z} \right)\mathrm{d}y\mathrm{d}z + \left( \frac{\partial P}{\partial z} - \frac{\partial R}{\partial x} \right)\mathrm{d}z\mathrm{d}x + \left( \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} \right)\mathrm{d}x\mathrm{d}y
\end{aligned} = ∮ Γ P d x + Q d y + R d z Σ ∬ ( ∂ y ∂ R − ∂ z ∂ Q ) d y d z + ( ∂ z ∂ P − ∂ x ∂ R ) d z d x + ( ∂ x ∂ Q − ∂ y ∂ P ) d x d y
右手法则:当右手除拇指外的四指沿 Γ \varGamma Γ Σ \varSigma Σ Γ \varGamma Γ Σ \varSigma Σ
斯托克斯公式可以被表示为行列式的形式:
∮ Γ P d x + Q d y + R d z = ∬ Σ ∣ d y d z d z d x d x d y ∂ ∂ x ∂ ∂ y ∂ ∂ z P Q R ∣ = ∬ Σ ∣ cos α cos β cos γ ∂ ∂ x ∂ ∂ y ∂ ∂ z P Q R ∣ d S \begin{aligned}
& \oint_\varGamma P\mathrm{d}x + Q\mathrm{d}y + R\mathrm{d}z\\
= & \iint\limits_\varSigma \begin{vmatrix}
\mathrm{d}y\mathrm{d}z & \mathrm{d}z\mathrm{d}x & \mathrm{d}x\mathrm{d}y \\
\dfrac{\partial}{\partial x} & \dfrac{\partial}{\partial y} & \dfrac{\partial}{\partial z} \\
P & Q & R
\end{vmatrix}\\
= & \iint\limits_\varSigma \begin{vmatrix}
\cos\alpha & \cos\beta & \cos\gamma \\
\dfrac{\partial}{\partial x} & \dfrac{\partial}{\partial y} & \dfrac{\partial}{\partial z} \\
P & Q & R
\end{vmatrix}\mathrm{d}S
\end{aligned} = = ∮ Γ P d x + Q d y + R d z Σ ∬ d y d z ∂ x ∂ P d z d x ∂ y ∂ Q d x d y ∂ z ∂ R Σ ∬ cos α ∂ x ∂ P cos β ∂ y ∂ Q cos γ ∂ z ∂ R d S
其中 n = ( cos α , cos β , cos γ ) \bm{n} = (\cos\alpha, \cos\beta, \cos\gamma) n = ( cos α , cos β , cos γ ) Σ \varSigma Σ
旋度(rotation): 设向量场
A ( x , y , z ) = P ( x , y , z ) i + Q ( x , y , z ) j + R ( x , y , z ) k \bm{A}(x, y, z) = \bm{P}(x, y, z)\bm{i} + \bm{Q}(x, y, z)\bm{j} + \bm{R}(x, y, z)\bm{k}
A ( x , y , z ) = P ( x , y , z ) i + Q ( x , y , z ) j + R ( x , y , z ) k
其中函数 P , Q , R P, Q, R P , Q , R
( ∂ R ∂ y − ∂ Q ∂ z ) i + ( ∂ P ∂ z − ∂ R ∂ x ) j + ( ∂ Q ∂ x − ∂ P ∂ y ) k \left( \frac{\partial R}{\partial y} - \frac{\partial Q}{\partial z} \right)\bm{i} + \left( \frac{\partial P}{\partial z} - \frac{\partial R}{\partial x} \right)\bm{j} + \left( \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} \right)\bm{k}
( ∂ y ∂ R − ∂ z ∂ Q ) i + ( ∂ z ∂ P − ∂ x ∂ R ) j + ( ∂ x ∂ Q − ∂ y ∂ P ) k
称为向量场 A \bm{A} A r o t A \mathrm{rot}\bm{A} rot A
r o t A = ∣ i j k ∂ ∂ x ∂ ∂ y ∂ ∂ z P Q R ∣ \mathrm{rot}\bm{A} = \begin{vmatrix}
\bm{i} & \bm{j} & \bm{k} \\
\dfrac{\partial}{\partial x} & \dfrac{\partial}{\partial y} & \dfrac{\partial}{\partial z} \\
P & Q & R
\end{vmatrix} rot A = i ∂ x ∂ P j ∂ y ∂ Q k ∂ z ∂ R
斯托克斯公式可以用旋度来定义:
∮ Γ A ⋅ d s = ∬ Σ r o t A ⋅ d S \oint_\varGamma \bm{A} \cdot \mathrm{d}\bm{s} = \iint\limits_\varSigma \mathrm{rot}\bm{A} \cdot \mathrm{d}\bm{S}
∮ Γ A ⋅ d s = Σ ∬ rot A ⋅ d S