数学分析初步（三）：一元函数积分

不定积分

对于任意一个由函数求导后得到的导函数，可以求出其原函数，原函数可以有无穷多个。假如 $F$ 是 $f$ 的一个原函数，那么 $F+C$ 也是 $f$ 的原函数， $C$ 被称为积分常数， $f$ 的任何两个原函数之间都相差一个常数。

连续函数必有原函数，如果一个函数在区间上存在间断点，则其在区间上必没有原函数。

原函数的全体被称作不定积分（Indefinite integral），它是微分的逆运算，记作：$\int f(x)\mathrm{d}x=F(x)+C$

不定积分和微分满足以下关系：

$$\frac{\mathrm{d}}{\mathrm{d}x}\int f(x)\mathrm{d}x=f(x)\\ \mathrm{d}\int f(x)\mathrm{d}x=f(x)\mathrm{d}x\\ \int F'(x)\mathrm{d}x=F(x)+C\\ \int \mathrm{d}F(x)=F(x)+C$$

不定积分具有线性运算的性质：

$$\int(k_1f_1(x)+k_2f_2(x))\mathrm{d}x=k_1\int f_1(x)\mathrm{d}x+k_2\int f_2(x)\mathrm{d}x$$

基本积分表

1. $\int k\mathrm{d}x=kx+C$

指对幂形式：

2. $\int x^\alpha\mathrm{d}x=\frac{x^{\alpha+1}}{\alpha+1}+C$
3. $\int\frac{1}{x}\mathrm{d}x$=$\ln|x|+C$
4. $\int e^x\mathrm{d}x=e^x+C$
5. $\int a^x\mathrm{d}x=\frac{a^x}{\ln x}+C$
6. $\int\ln x\mathrm{d}x=x\ln x-x+C$

三角函数形式：

7. $\int\cos ax\mathrm{d}x=\frac{1}{a}\sin ax+C$
8. $\int\sin ax\mathrm{d}x=-\frac{1}{a}\cos ax+C$
9. $\int\sec^2x=\tan x+C$
10. $\int\csc^2x\mathrm{d}x=-\cot x+C$
11. $\int\sec x\tan x\mathrm{d}x=\sec x+C$
12. $\int\csc x\cot x\mathrm{d}x=-\csc x+C$

反三角函数形式：

13. $\int\frac{\mathrm{d}x}{\sqrt{1-x^2}}=\arcsin x+C=-\arccos x+C_1$
14. $\int\frac{\mathrm{d}x}{1+x^2}=\arctan x+C=-\mathrm{arccot} x+C_1$

复合形式：

15. $\int\tan x\mathrm{d}x=-\ln|\cos x|+C$
16. $\int\cot x\mathrm{d}x=\ln|\sin x|+C$
17. $\int\sec x\mathrm{d}x=\ln|\sec x+\tan x|+C=\frac{1}{2}\ln|\frac{1+\sin x}{1-\sin x}|+C$
18. $\int\csc x\mathrm{d}x=\ln|\csc x-\cot x|+C=\ln|\tan\frac{x}{2}|+C$
19. $\int\frac{1}{a^2+x^2}\mathrm{d}x=\frac{1}{a}\arctan\frac{x}{a}+C$
20. $\int\frac{1}{x^2-a^2}\mathrm{d}x=\frac{1}{2a}\ln|\frac{x-a}{x+a}|+C$
21. $\int\frac{1}{\sqrt{a^2-x^2}}\mathrm{d}x=\arcsin\frac{x}{a}+C$
22. $\int\frac{1}{\sqrt{x^2+a^2}}\mathrm{d}x=\ln|x+\sqrt{x^2+a^2}|+C$
23. $\int\frac{1}{\sqrt{x^2-a^2}}\mathrm{d}x=\ln|x+\sqrt{x^2-a^2}|+C$
24. $\int\sqrt{a^2-x^2}\mathrm{d}x=\frac{a^2}{2}\arcsin\frac{x}{a}+\frac{1}{2}x\sqrt{a^2-x^2}+C$

常见的原函数不是初等函数的情形：

1. $\int e^{ax^2}\mathrm{d}x\quad(a\neq 0)$
2. $\int\frac{\sin x}{x}\mathrm{d}x$
3. $\int\frac{\cos x}{x}\mathrm{d}x$
4. $\int\sin x^2\mathrm{d}x$
5. $\int\cos x^2\mathrm{d}x$
6. $\int\frac{x^n}{\ln x}\mathrm{d}x\quad(n\neq-1)$
7. $\int\frac{\ln x}{x+a}\mathrm{d}x\quad(a\neq 0)$
8. $\int(\sin x)^n\mathrm{d}x\quad(n\notin\mathbb{Z})$
9. $\int\frac{1}{\sqrt{x^4+a}}\mathrm{d}x\quad(a\neq 0)$
10. $\int\sqrt{1+k(\sin x)^2}\mathrm{d}x\quad(k\neq 0,k\neq -1)$
11. $\int\frac{1}{\sqrt{1+k(\sin x)^2}}\mathrm{d}x\quad(k\neq 0,k\neq -1)$

换元积分法

第一换元积分法：

我们由复合函数求导法则 $(f(\varphi(t)))'=f'(\varphi(t))\varphi'(t)$ 可知：

$$\int f'(\varphi(t))\varphi'(t)=f(\varphi(t))+C$$

由此得到第一换元积分法的基本公式，这个不定积分也可以记作：

$$\int f(\varphi(t))\varphi'(t)\mathrm{d}t=\int f(\varphi(t))\mathrm{d}\varphi(t)$$

可以看出，由 $\varphi'(t)\mathrm{d}t$ 转化为 $\mathrm{d}\varphi(t)$ 是一个求原函数的过程，由 $\mathrm{d}\varphi(t)$ 转化为 $\varphi'(t)\mathrm{d}t$ 是一个求导的过程。

常数可以在积分号和微分号中随意移动，例如：

$$a\int f(x)\mathrm{d}x=\int af(x)\mathrm{d}x=\int f(x)\mathrm{d}ax$$

微分号后面随意加减常数不会对式子产生影响（因为常数项求导后消去）：

$$\int f(x)\mathrm{d}x=\int f(x)\mathrm{d}(x\pm a)$$

常用的配元形式：

1. $\int f(ax+b)\mathrm{d}x=\frac{1}{a}\int f(ax+b)\mathrm{d}(ax+b)$

万能凑幂法：

2. $\int f(x^n)x^{n-1}\mathrm{d}x=\frac{1}{n}\int f(x^n)\mathrm{d}x^n$
3. $\int f(x^n)\frac{1}{x}\mathrm{d}x=\frac{1}{n}\int f(x^n)\frac{1}{x^n}\mathrm{d}x^n$

含自然常数：

4. $\int f(e^x)e^x\mathrm{d}x=\int f(e^x)\mathrm{d}e^x$
5. $\int f(\ln x)\frac{1}{x}\mathrm{d}x=\int f(\ln x)\mathrm{d}\ln x$

含三角函数：

6. $\int f(\sin x)\cos x\mathrm{d}x=\int f(\sin x)\mathrm{d}\sin x$
7. $\int f(\cos x)\sin x\mathrm{d}x=-\int f(\cos x)\mathrm{d}\cos x$
8. $\int f(\tan x)\sec^2x\mathrm{d}x=\int f(\tan x)\mathrm{d}\tan x$

第二换元积分法：

第二换元积分法将非复合函数积分转化为复合函数积分的形式，公式如下：

$$\int f(x)\mathrm{d}x=\int f(\varphi(t))\mathrm{d}\varphi(t)=\int f(\varphi(t))\varphi'(t)\mathrm{d}t=F(t)+C$$

完成积分后将原变量进行回代，得到：

$$F(t)+C=F(\varphi^{-1}(x))+C$$

常见类型：

1. $\int f(x,\sqrt[n]{ax+b})\mathrm{d}x$ ，令 $t=\sqrt[n]{ax+b}$
2. $\int f(x,\sqrt[n]{\frac{ax+b}{cx+d}})\mathrm{d}x$ ，令 $t=\sqrt[n]{\frac{ax+b}{cx+d}}$
3. $\int f(x,\sqrt{a^2-x^2})\mathrm{d}x$ ，令 $x=a\sin t$ 或 $x=a\cos t$
4. $\int f(x,\sqrt{a^2+x^2})\mathrm{d}x$ ，令 $x=a\tan t$ 或 $x=a\sh t$
5. $\int f(x,\sqrt{x^2-a^2})\mathrm{d}x$ ，令 $x=a\sec t$ 或 $x=a\ch t$
6. $\int f(a^x)\mathrm{d}x$ ，令 $t=a^x$

分母中因子次数较高时，可以尝试倒代换。

分部积分法

我们由函数乘积求导法则 $(uv)'=u'v+uv'$ 可知：

$$\int u(x)v'(x)\mathrm{d}x+\int u'(x)v(x)\mathrm{d}x=u(x)v(x)$$

由此得到分部积分法的基本公式：

$$\int u(x)v'(x)\mathrm{d}x=u(x)v(x)-\int u'(x)v(x)\mathrm{d}x$$

将 $v'(x)$ 和 $u'(x)$ 拿到微分号后面，也可以记作：

$$\int u(x)\mathrm{d}v(x)=u(x)v(x)-\int v(x)\mathrm{d}u(x)$$

在分部积分时选取 $u$ 和 $v$ 的原则：$v'$ 的原函数容易求， $\int v\mathrm{d}u$ 的形式比 $\int u\mathrm{d}v$ 更简单。

选取 $v'$ 的优先级顺序（从大到小）：

1. 指数函数
2. 三角函数
3. 幂函数
4. 对数函数
5. 反三角函数

循环积分：

以下演示了一个循环积分的经典例子：

$$\begin{aligned} \int e^x\cos x\mathrm{d}x=&\int \cos x\mathrm{d}e^x\\ =&e^x\cos x-\int e^x\mathrm{d}\cos x\\ =&e^x\cos x+\int\sin x\mathrm{d}e^x\\ =&e^x\cos x+e^x\sin x-\int e^x\cos x\mathrm{d}x\\ \end{aligned}\\ 2\int e^x\cos x\mathrm{d}x=e^x\cos x+e^x\sin x\\ \int e^x\cos x\mathrm{d}x=\frac{1}{2}e^x(\cos x+\sin x)$$

当多次分部积分后出现重复的积分项时，就可以藉由重复项求出所要求积分的值。

有理函数积分

有理函数又被称作有理分式（Rational fraction），是指分子和分母都是多项式的分式，一般形式如下：

$$R(x)=\frac{P(n)}{Q(n)}=\frac{\alpha_0x^n+\alpha_1x^{n-1}+\cdots +\alpha_n}{\beta_0x^m+\beta_1x^{m-1}+\cdots +\beta_m}$$

有理分式被分为真分式和假分式两种：

真分式：分母上多项式的最高次数大于分子上多项式的最高次数，即 $m>n$ ；
假分式：分母上多项式的最高次数小于等于分子上多项式的最高次数，即 $m\leq n$ 。

所谓有理函数求积分，就是指将原来的假分式拆成真分式和多项式相加的形式，再将真分式拆成多个部分分式，以便于求解积分，有理函数的原函数都是初等函数。

多项式除法

多项式除法是代数中的一种算法，用一个同次或低次的多项式去除另一个多项式，是一个经常被用于因式分解的技巧，这里我们将它用于分解假分式。

多项式除法的基本思路：

1. 把被除式，除式按某个字母作降幂排列，缺项补零。
2. 将分子的第一项除以分母的最高次项，得到首商，写在横线之上。
3. 将分母乘以首商，乘积写在分子前两项之下（同类项对齐）。
4. 从分子的相应项中减去刚得到的乘积（消去相等项，把不相等的项结合起来），得到的余式写在下面。
5. 重复以上步骤，直到最后只剩常数，得出结果。

例： 计算 $\frac{x^3-12x^2-42}{x-3}$ 。

$$\begin{array}{ll} &\ x^2-9x-27\\ x-3 \!\!\!\!\!\!&\overline{)x^3-12x^2+0x-42} \\ &\underline{\ x^3-\ \ 3x^2}\\ &\quad\quad\ -9x^2+0x\\ &\quad\quad\ \underline{-9x^2+27x}\\ &\quad\quad\quad\quad\quad-27x^2-42\\ &\quad\quad\quad\quad\quad\underline{-27x^2+81}\\ &\quad\quad\quad\quad\quad\quad\quad\ \ \ -123\\ \end{array}$$

综上所述：

$$\frac{x^3-12x^2-42}{x-3}=x^2-9x-27-\frac{123}{x-3}$$

真分式分解

当分母上的多项式形如多个一次式和二次式相乘时，可以进行真分式分解：

$$Q(x)=(a_1x-b_1)^{\lambda_1}\cdots (a_sx-b_s)^{\lambda_s}(m_1x^2+p_1x+q_1)^{u_1}\cdots (m_tx^2+p_tx+q_t)^{u_t}$$

其中对于任意二次式，满足 $\Delta=p_j^2-4q_j<0$ ，这代表它是一个无法进行因式分解的二次式（如果可以因式分解，则需要分解后充当一次式）。

一次式分解：

对于形如 $\frac{P(x)}{(ax+b)^k}$ 的 $k$ 重一次式，可以采用如下分解方式：
当 $k=1$ 时：

$$\frac{P(x)}{(a_1x+b_1)(a_2x+b_2)\cdots (a_nx+b_n)}=\frac{A_1}{a_1x+b_1}+\frac{A_2}{a_2x+b_2}+\cdots +\frac{A_n}{a_nx+b_n}$$

当 $k>1$ 时：

$$\frac{P(x)}{(ax+b)^k}=\frac{A_1}{ax+b}+\frac{A_2}{(ax+b)^2}+\cdots +\frac{A_k}{(ax+b)^k}$$

二次式分解：

对于形如 $\frac{P(x)}{(mx^2+px+q)^k}$ 的 $k$ 重二次式，可以采用如下分解方式：

当 $k=1$ 时：

$$\frac{P(x)}{(m_1x^2+p_1x+q_1)\cdots (m_nx^2+p_nx+q_n)}=\frac{A_1x+B_1}{m_1x^2+p_1x+q_1}++\cdots +\frac{A_nx+B_n}{m_nx^2+p_nx+q_n}$$

当 $k>1$ 时：

$$\frac{P(x)}{(mx^2+px+q)^k}=\frac{A_1x+B_1}{mx^2+px+q}+\frac{A_2x+B_2}{(mx^2+px+q)^2}+\cdots +\frac{A_kx+B_k}{(mx^2+px+q)^k}$$

例： 求 $\int\frac{x^2+1}{(x+2)(x+1)^2}\mathrm{d}x$

首先进行真分式分解：

$$\frac{x^2+1}{(x+2)(x+1)^2}=\frac{A}{x+2}+\frac{B}{x+1}+\frac{C}{(x+1)^2}$$

将各分式通分后合并：

$$\frac{A}{x+2}+\frac{B}{x+1}+\frac{C}{(x+1)^2}=\frac{A(x+1)^2+B(x+1)(x+2)+C(x+2)}{(x+2)(x+1)^2}$$

接下来求解待定系数，主要使用以下两种方法：

反解方程法：

将分子与原式的分子系数作比对, 写出关于待定系数的方程, 进行求解。

$$A(x+1)^2+B(x+1)(x+2)+C(x+2)=(A+B)x^2+(2A+3B+C)x+A+2B+2C\\ (A+B)x^2+(2A+3B+C)x+A+2B+2C=x^2+1$$

$$\left\{\begin{aligned}&A+B=1\\&2A+3B+C=0\\&A+2B+2C=1\end{aligned}\right.$$

$$\left\{\begin{aligned}&A=5\\&B=-4\\&C=2\end{aligned}\right.$$

实根代入法：

向原式中代入 $x=-1$ ，可以消掉 $A,B$ 项，解得：

$$C=(-1)^2+1=2$$

向原式中代入 $x=-2$ ，可以消掉 $B,C$ 项，解得：

$$A(-1)^2=(-2)^2+1\\A=5$$

将 $A,C$ 的值代回原式中，求出 $B=-4$ 。

综上所述：

$$\int\frac{x^2+1}{(x+2)(x+1)^2}\mathrm{d}x=\int\frac{5}{x+2}\mathrm{d}x-\int\frac{4}{x+1}\mathrm{d}x+\int\frac{2}{(x+1)^2}\mathrm{d}x$$

部分分式积分

一次式积分：

$\int\frac{A}{x-a}\mathrm{d}x=A\ln|x-a|+C\\ \int\frac{A}{(x-a)^k}\mathrm{d}x=\frac{A}{1-n}(x-a)^{1-n}+C\quad(n\neq 1)$

二次式积分：

对于 $\int\frac{Cx+D}{(x^2+px+q)^k}\mathrm{d}x\ (p^2-4q<0)$ ，先将二次式进行配方：

$$\begin{aligned}x^2+px+q=&x^2+2\cdot\frac{p}{2}x+\frac{p^2}{4}-\frac{p^2}{4}+q\\=&(x+\frac{p}{2})^2+q-\frac{p^2}{4}\end{aligned}$$

令 $t=x+\frac{p}{2},r^2=q-\frac{p^2}{4}$

然后对分母进行配凑：

$$\begin{aligned}Cx+D=&C(x+\frac{p}{2})-C\frac{p}{2}+D\\=&Ct-\frac{Cp}{2}+D\end{aligned}$$

因此原式可以换元成：

$$\begin{aligned}\int\frac{Cx+D}{(x^2+px+q)^k}\mathrm{d}x=&\int\frac{Ct-\frac{Cp}{2}+D}{(t^2+r^2)^k}\mathrm{d}x\\ =&C\int\frac{t\mathrm{d}t}{(t^2+r^2)^k}+(D-\frac{Cp}{2})\int\frac{\mathrm{d}t}{(t^2+r^2)^k}\end{aligned}$$

当 $k=1$ 时：

$$\int\frac{t\mathrm{d}t}{t^2+r^2}=\frac{1}{2}\int\frac{\mathrm{d}(t^2+r^2)}{t^2+r^2}=\frac{1}{2}\ln(t^2+r^2)+C$$

$$\int\frac{\mathrm{d}t}{t^2+r^2}=\frac{1}{r}\int\frac{1}{(\frac{t}{r})^2+1}\mathrm{d}(\frac{t}{r})=\frac{1}{r}\arctan\frac{t}{r}+C$$

当 $k>1$ 时：

$$\int\frac{t\mathrm{d}t}{(t^2+r^2)^k}=\frac{1}{2}\int\frac{\mathrm{d}(t^2+r^2)}{(t^2+r^2)^k}=\frac{1}{2}\frac{1}{1-k}(t^2+r^2)^{1-k}+C$$

$$\begin{aligned}I_k=\int\frac{\mathrm{d}t}{(t^2+r^2)^k}=&\frac{1}{r^2}\int\frac{t^2+r^2-t^2}{(t^2+r^2)^k}\mathrm{d}t\\ =&\frac{1}{r^2}\int\frac{\mathrm{d}t}{(t^2+r^2)^{k-1}}-\frac{1}{r^2}\int\frac{t^2\mathrm{d}t}{(t^2+r^2)^k}\\ =&\frac{1}{r^2}I_{k-1}-\frac{1}{1-k}\frac{1}{2}\int t\mathrm{d}(t^2+r^2)^{1-k}\\ =&\frac{1}{r^2}I_{k-1}-\frac{1}{2r^2(k-1)}\left[\frac{t}{(t^2+r^2)^{k-1}}-I_{k-1}\right] \end{aligned}$$

有理代换

对于一些非有理函数积分，我们也可以将其转换为有理函数求解，常见的有三角代换和根式代换。

三角代换：

设 $R(\sin x,\cos x)$ 表示三角函数有理式，要求 $\int R(\sin x,\cos x)\mathrm{d}x$ ，则令 $t=\tan\frac{x}{2}$ ，将原积分转换为 $t$ 的有理函数的积分，这种换元方法被称为万能代换。

$$\sin x=\frac{2\sin\frac{x}{2}\cos\frac{x}{2}}{\sin^2\frac{x}{2}+\cos^2\frac{x}{2}}=\frac{2\tan\frac{x}{2}}{1+\tan^2\frac{x}{2}}=\frac{2t}{1+t^2}$$

$$\cos x=\frac{\cos^2\frac{x}{2}-\sin^2\frac{x}{2}}{\sin^2\frac{x}{2}+\cos^2\frac{x}{2}}=\frac{1-\tan^2\frac{x}{2}}{1+\tan^2\frac{x}{2}}=\frac{1-t^2}{1+t^2}$$

但在某些情况下，可以选择更方便的变量进行代换，例如以下三种情况：

1. 若被积函数是关于 $\sin x$ 的奇函数，即 $R(-\sin x,\cos x)=-R(\sin x,\cos x)$ ，可令 $t=\cos x$ 。
2. 若被积函数是关于 $\cos x$ 的奇函数，即 $R(\sin x,-\cos x)=-R(\sin x,\cos x)$ ，可令 $t=\sin x$ 。
3. 若被积函数同时是关于 $\sin x$ 和 $\cos x$ 的偶函数，即 $R(-\sin x,-\cos x)=R(\sin x,\cos x)$ ，可令 $t=\tan x$ 。

根式代换：

被积函数为简单根式的有理式，可通过根式代换转换为有理函数的积分：

1. $\int R(x,\sqrt[n]{ax+b})\mathrm{d}x$ ，令 $t=\sqrt[n]{ax+b}$
2. $\int R(x,\sqrt[n]{\frac{ax+b}{cx+d}})\mathrm{d}x$ ，令 $t=\sqrt[n]{\frac{ax+b}{cx+d}}$
3. $\int R(x,\sqrt[n]{ax+b},\sqrt[m]{ax+b})\mathrm{d}x$ ，令 $t=\sqrt[p]{ax+b}$ ， $p$ 为 $m,n$ 的最小公倍数。

定积分

在很多数学和物理问题中，经常需要求解一种特殊和式的极限：

$$\lim_{||T||\rightarrow 0}\sum_{i=1}^nf(\xi_i)\Delta x_i$$

这就引出了定积分（Definite integral） 的概念。

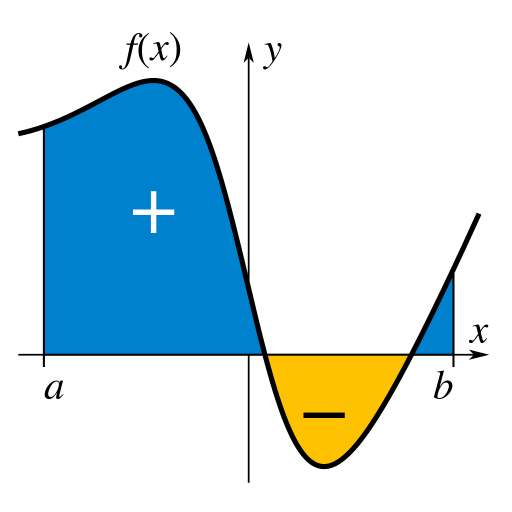
用微元法求函数图像与坐标轴之间围成的图形的面积：

1. 分割

在区间 $[a,b]$ 中任意插入 $n-1$ 个分点：

$$a=x_0<x_1<x_2<\cdots <x_{n-1}<x_n=b$$

$$\Delta_i=[x_i,x_i],\Delta x_i=x_i-x_{i-1},i=1,2,3,\cdots ,n$$

用直线 $x=x_i$ 将曲边梯形分成 $n$ 个小曲边梯形。

这个分割记作 $T=\{x_0,x_1,\cdots ,x_n\}$ 或 $T=\{\Delta_0,\cdots ,\Delta_n\}$ 。

2. 近似

把小曲边梯形 $A_i$ 近似看作矩形，即任取 $\xi\in[x_{i-1},x_i]$ ，在 $[x_{i-1},x_i]$ 上把 $f(x)$ 近似看作常数 $f(\xi_i)$ ，此时 $A_i$ 的面积 $S_i$ 约为 $f(\xi_i)\Delta x_i$ ，所以：

$$S(A)=\sum_{i=1}^nS_i\approx\sum_{i=1}^nf(\xi_i)\Delta x_i$$

上述和式 $\sum_{i=1}^nf(\xi_i)\Delta x_i$ 称为积分和或黎曼和。

3. 逼近

近似得出的黎曼和和曲边梯形的面积 $S$ 总有差别，当分割越来越细时，黎曼和与 $S$ 的差距就会越来越小。

分割 $T$ 的细度（模）：

$$||T||=\max\{\Delta x_i|i=1,2,\cdots ,n\}$$

则当 $||T||\rightarrow 0$ 时，就能保证分割越来越细。

对于给定的 $\varepsilon>0$ ，能够找到 $\delta>0$ ，使得当
$||T||<\delta$ 时，对任意 $\xi_i\in[x_{i-1},x_i]$ ，都有：

$$|\sum_{i=1}^nf(\xi_i)\Delta x_i-S|<\varepsilon$$

定积分的定义：

设 $f$ 是定义在 $[a,b]$ 上的函数， $J\in R$ ，
若 $\forall\varepsilon>0$ ， $\exists\delta>0$ ，对任意分割

$$T:a=x_0<x_1<\cdots <x_{n-1}<x_n=b$$

及任意 $\xi_i\in[x_{i-1},x_i],i=1,2,\cdots ,n$ ，
当 $||T||=\max{\Delta x_i}<\delta$ 时，必有

$$|\sum_{i=1}^nf(\xi_i)\Delta x_i-J|<\varepsilon$$

则称 $f$ 在 $[a,b]$ 上可积，并称 $J$ 为 $f$ 在 $[a,b]$ 上的定积分，记作：

$$J=\int_a^bf(x)\mathrm{d}x=\lim_{||T||\rightarrow 0}\sum_{i=1}^nf(\xi_i)\Delta x_i$$

$[a,b]$ 是积分区间， $b$ 称为积分上限， $a$ 称为积分下限， $f(x)\mathrm{d}x$ 称为被积表达式。

定积分的值仅与被积函数和积分区间有关，而与积分量无关。

定积分的估值

设 $f(x)\in C[a,b]$ ，则 $\int_a^bf(x)\mathrm{d}x$ 存在，根据定积分定义可得如下近似计算方法：

将 $[a,b]$ 分成 $n$ 等份， $\Delta x=\frac{b-a}{n}$ ， $x_i=a+i\cdot\Delta x\ (i=0,1,\cdots ,n)$

记 $f(x_i)=y_i$ ，有以下三种定积分估值方法：

左矩形公式：

$$\begin{aligned}\int_a^bf(x)\mathrm{d}x\approx&y_0\Delta x+y_1\Delta x+\cdots +y_{n-1}\Delta x\\=&\frac{b-a}{n}(y_0+y_1+\cdots +y_{n-1})\end{aligned}$$

右矩形公式：

$$\begin{aligned}\int_a^bf(x)\mathrm{d}x\approx&y_1\Delta x+y_2\Delta x+\cdots +y_n\Delta x\\=&\frac{b-a}{n}(y_1+y_2+\cdots +y_n)\end{aligned}$$

梯形公式：

$$\begin{aligned}\int_a^bf(x)\mathrm{d}x\approx&\sum_{i=1}^{n-1}\frac{1}{2}[y_{i-1}+y_i]\Delta x\\=&\frac{b-a}{n}\left[\frac{1}{2}(y_0+y_n)+(y_1+\cdots +y_{n-1})\right]\end{aligned}$$

沃利斯公式（Wallis formula）：

$$\frac{\pi}{2}=\lim_{n\rightarrow\infty}\left[\frac{(2n)!!}{(2n-1)!!}\right]^2\frac{1}{2n+1}$$

其中 $n!!$ 为双阶乘，表示不超过这个正整数且与它有相同奇偶性的所有正整数乘积。
沃里斯公式通常用来简化定积分计算：

$$\int_0^{\frac{\pi}{2}}\sin^nx=\int_0^{\frac{\pi}{2}}\cos^nx=\left\{\begin{aligned}&\frac{(n-1)!!}{n!!}\cdot\frac{\pi}{2}&,n为偶数\\&\frac{(n-1)!!}{n!!}&,n为奇数\end{aligned}\right.$$

定积分的性质

（以下所列定积分均存在）

1. 上下限可换： $\int_a^bf(x)\mathrm{d}x=-\int_b^af(x)\mathrm{d}x\qquad\int_a^af(x)\mathrm{d}x=0$

2. 常值函数积分： $\int_a^bk\mathrm{d}x=k(b-a)$

3. 常数可分离到积分号外部： $\int_a^bkf(x)\mathrm{d}x=k\int_a^bf(x)\mathrm{d}x$

4. 线性运算： $\int_a^b[f(x)\pm g(x)]\mathrm{d}x=\int_a^bf(x)\mathrm{d}x\pm\int_a^bg(x)\mathrm{d}x$
   藉由定积分的极限定义可以证明线性运算性质：

$$\begin{aligned}左端=&\lim_{||T||\rightarrow 0}\sum_{i=1}^n[f(\xi_i)\pm g(\xi_i)]\Delta x_i\\ =&\lim_{||T||\rightarrow 0}\sum_{i=1}^nf(\xi_i)\Delta x_i\pm\lim_{||T||\rightarrow 0}\sum_{i=1}^ng(\xi_i)\Delta x_i=右端\end{aligned}$$

5. 函数 $f,g$ 在区间上可积，其乘积 $f\cdot g$ 在该区间上依旧可积。

6. 积分区间的可加性： $f$ 在 $[a,b]$ 上可积的充要条件是 $\forall c\in(a,b)$ ， $f$ 在 $[a,c]$ 和 $[c,b]$ 上都可积，此时有：

$$\int_a^bf(x)\mathrm{d}x=\int_a^cf(x)\mathrm{d}x+\int_c^bf(x)\mathrm{d}x$$

7. 积分的保号性：若在 $[a,b]$ 上 $f(x)\geq 0$ ，则 $\int_a^bf(x)\mathrm{d}x\geq 0$ 。
   证明：

$$\begin{aligned}由&\sum_{i=1}^ng(\xi_i)\Delta x_i\geq 0\\ 可得&\int_a^bf(x)\mathrm{d}x=\lim_{||T||\rightarrow 0}\sum_{i=1}^ng(\xi_i)\Delta x_i\geq 0\end{aligned}$$

• 推论：若在 $[a,b]$ 上 $f(x)\leq g(x)$ ，则 $\int_a^bf(x)\mathrm{d}x\leq\int_a^bg(x)\mathrm{d}x$

8. 绝对值定理： $|\int_a^bf(x)\mathrm{d}x|\leq\int_a^b|f(x)|\mathrm{d}x\quad(a<b)$
   证明：

$$\begin{aligned}由&-|f(x)|\leq f(x)\leq|f(x)|\\ 可得&-\int_a^b|f(x)|\mathrm{d}x\leq\int_a^bf(x)\mathrm{d}x\leq\int_a^b|f(x)|\mathrm{d}x\\ 即&|\int_a^bf(x)\mathrm{d}x|\leq\int_a^b|f(x)|\mathrm{d}x\end{aligned}$$

9. 估值定理：设 $M=\max\limits_{[a,b]}f(x),m=\min\limits_{[a,b]}f(x)$ ，则

$$m(b-a)\leq\int_a^bf(x)\mathrm{d}x\leq M(b-a)\quad(a<b)$$

证明：由连续函数最值定理可以得到 $f(x)$ 必存在最大值 $M$ 和最小值 $m$ ，即 $\exists x\in[a,b]$ ，使得 $m\leq f(x)\leq M$ ，所以：

$$\int_a^bm\mathrm{d}x\leq\int_a^bf(x)\mathrm{d}x\leq\int_a^bM\mathrm{d}x\\ m(b-a)\leq\int_a^bf(x)\mathrm{d}x\leq M(b-a)$$

积分第一中值定理

若 $f(x)\in C[a,b]$ ，则存在至少一点 $\xi\in[a,b]$ ，使

$$\int_a^bf(x)\mathrm{d}x=f(\xi)(b-a)$$

证明：

设 $f(x)$ 在 $[a,b]$ 上的最小值和最大值分别是 $m$ 和 $M$ ，则由估值定理可得：

$$m\leq\frac{1}{a-b}\int_a^bf(x)\mathrm{d}x\leq M$$

根据闭区间上连续函数介值定理，在 $[a,b]$ 上至少存在一点 $\xi\in[a,b]$ ，使得

$$f(\xi)=\frac{1}{a-b}\int_a^bf(x)\mathrm{d}x$$

因此

$$\int_a^bf(x)\mathrm{d}x=f(\xi)(b-a)$$

其中 $f(\xi)$ 可以理解为 $f(x)$ 在 $[a,b]$ 上所有函数值的平均值，称作积分均值，这是有限个数的算术平均数的推广。

推论： 若 $f,g$ 在 $[a,b]$ 上连续，且 $g(x)$ 在 $[a,b]$ 上不变号，则 $\exists\xi\in[a,b]$ ，使

$$\int_a^bf(x)g(x)\mathrm{d}x=f(\xi)\int_a^bg(x)\mathrm{d}x$$

证明：令

$$F(x)=\int_a^xf(t)g(t)\mathrm dt\\ G(x)=\int_a^xg(t)\mathrm dt$$

这两个函数均在 $[a,b]$ 上可导，且 $g(x)\neq 0$，即 $F'(x)$ 和 $G'(x)$ 不同时为零，并且

$$G(x)\neq 0=G(a)$$

由柯西中值定理可得：

$$\frac{F'(\xi)}{G'(\xi)}=\frac{F(b)-F(a)}{G(b)-G(a)}=\frac{F(b)}{G(b)}$$

又因为

$$\frac{F'(\xi)}{G'(\xi)}=\frac{f(\xi)g(\xi)}{g(\xi)}=f(\xi)$$

可得

$$\int_a^bf(x)g(x)\mathrm{d}x=f(\xi)\int_a^bg(x)\mathrm{d}x$$

可积条件

定义： 设 $f$ 在 $[a,b]$ 上有界，对任意分割

$$T:a=x_0<x_1<\cdots<x_n=b$$

称 $S(T)=\sum_{i=1}^nM_i\Delta x_i$ 为 $f$ 关于分割 $T$ 的达布上和，其中

$$M_i=\sup\{f(x)|x\in[x_{i-1},x_i]\},\ i=1,2,\cdots,n$$

称 $s(T)=\sum_{i=1}^nm_i\Delta x_i$ 为 $f$ 关于分割 $T$ 的达布下和，其中

$$m_i=\inf\{f(x)|x\in[x_{i-1},x_i]\},\ i=1,2,\cdots,n$$

称 $\omega_i=M_i-m_i\ (i=1,2,\cdots,n)$ 为 $f$ 在 $[x_{i-1},x_i]$ 上的振幅。
振幅反映了函数在区间内的变化范围，是一个与连续性相关联的概念。

可积准则： 函数 $f$ 在 $[a,b]$ 上可积的充要条件是：$\forall\varepsilon>0$，$\exists$ 分割 $T$，使

$$S(T)-s(T)=\sum_{i=1}^n(M_i-m_i)\Delta x_i=\sum_{i=1}^n\omega_i\Delta x_i<\varepsilon$$

下面介绍了可积准则的三个应用情形，分别可以推出一条定积分存在定理。

情形一： 每个 $\omega_i<\dfrac{\varepsilon}{b-a}$，从而

$$\sum_{i=1}^n\omega_i\Delta x_i<\frac{\varepsilon}{b-a}\sum_{i=1}^n\Delta x_i=\varepsilon$$

情形二： 若 $\sum_{i=1}^n\omega_i$ 有界，即 $\exists M$，对任意分割 $T$，$\sum_{i=1}^n\omega_i\leq M$，则当 $||T||<\dfrac{\varepsilon}{M}$ 时，

$$\sum_{i=1}^n\omega_i\Delta x_i\leq||T||\sum_{i=1}^n\omega_i<\frac{\varepsilon}{M}M=\varepsilon$$

情形三： 若 $\sum\omega_i\Delta x_i=\sum\omega_i'\Delta x_i'+\sum\omega_i''\Delta x_i''$，

在 $\sum\omega_i'\Delta x_i'$ 中，

$$\omega_i'<\frac{\varepsilon}{2(b-a)}$$

而在 $\sum\omega_i''\Delta x_i''$ 中，

$$\sum\Delta x_i''<\frac{\varepsilon}{2(M-m)}$$

其中 $M-m$ 是 $f$ 在 $[a,b]$ 上的振幅，从而

$$\omega_i\leq M-m,i=1,2,\cdots,n$$

于是

$$\begin{aligned} \sum\omega_i\Delta x_i&=\sum\omega_i'\Delta x_i'+\sum\omega_i''\Delta x_i''\\ &<\frac{\varepsilon}{2(b-a)}(b-a)+\frac{\varepsilon}{2(M-m)}(M-m)\\ &=\varepsilon \end{aligned}$$

定积分存在定理：

1. 函数在闭区间内连续。
2. 函数在闭区间上单调。
3. 函数在闭区间内有界，且只有有限个间断点。

微积分学基本定理

变限积分

设 $f(x)$ 在 $[a,b]$ 上连续，并且设 $x$ 为 $[a,b]$ 上的一点，有这样的一个定积分： $\int_a^xf(t)\mathrm{d}t$ 。

如果上限 $x$ 在区间上任意变动，则对于每一个给定的 $x$ 值，都有一个对应得定积分值，这些值在区间上定义了一个函数，称为积分上限函数：

$$\Phi(x)=\int_a^xf(t)\mathrm{d}t$$

若 $f(x)\in C[a,b]$ ，则积分上限函数是 $f(x)$ 在 $[a,b]$ 上的一个原函数。

证明：$\forall x,x+h\in[a,b]$ ，则有

$$\begin{aligned}\frac{\Phi(x+h)-\Phi(x)}{h}=&\frac{1}{h}\left[\int_a^{x+h}f(t)\mathrm{d}t-\int_a^xf(t)\mathrm{d}t\right]\\ =&\frac{1}{h}\int_x^{x+h}f(t)\mathrm{d}t=f(\xi)\quad(x<\xi<x+h)\end{aligned}$$

由于 $f(x)\in C[a,b]$

$$\Phi'(x)=\lim_{h\rightarrow 0}\frac{\Phi(x+h)-\Phi(x)}{h}=\lim_{h\rightarrow 0}f(\xi)=f(x)$$

该定理为通过原函数计算定积分开辟了道路。

变限积分求导：

1. $\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}\int_a^xf(t)\mathrm{d}t=f(x)$
2. $\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}\int_x^bf(t)\mathrm{d}t=-f(x)$
3. $\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}\int_a^{\varphi(x)}f(t)\mathrm{d}t=f[\varphi(x)]\varphi'(x)$
4. $\displaystyle\frac{\mathrm{d}}{\mathrm{d}x}\int_{\psi(x)}^{\varphi(x)}f(t)\mathrm{d}t=\dfrac{\mathrm{d}}{\mathrm{d}x}\left[\int_{\psi(x)}^af(t)\mathrm{d}t+\int_a^{\varphi(x)}f(t)\mathrm{d}t\right]=f[\varphi(x)]\varphi'(x)-f[\psi(x)]\psi'(x)$

变限积分求导时，被积函数中若含有 $x$ ，要先将其从积分号中分离出来，再求导。

牛顿-莱布尼茨公式

设 $f(x)\in C[a,b]$ ，且 $F(x)$ 是 $f(x)$ 的原函数。

对于 $[a,b]$ 的任一分割 $T=\{a=x_0,x_1,\cdots ,x_n=b\}$ ，在每个小区间 $[x_{i-1},x_i]$ 上对 $F(x)$ 使用拉格朗日中值定理，则分别存在 $\eta_i\in(x_{i-1},x_i),i=1,2,\cdots ,n$ ，使得

$$\begin{aligned}F(b)-F(a)=&\sum_{i=1}^n[F(x_i)-F(x_{i-1})]\\ =&\sum_{i=1}^nF'(\eta_i)\Delta x_i\\ =&\sum_{i=1}^nf(\eta_i)\Delta x_i\end{aligned}$$

因为 $f(x)\in C[a,b]$ ，从而 $f(x)$ 在 $[a,b]$ 上一致连续，
所以 $\forall\varepsilon>0,\exists\delta>0$ ，当 $x',x''\in[a,b]$ 且 $|x'-x''|<\delta$ 时，有

$$|f(x')-f(x'')|<\frac{\varepsilon}{b-a}$$

于是，当 $\Delta x_i\leq||T||<\delta$ 时，任取 $\xi_i\in[x_{i-1},x_i]$ ，有 $|\xi_i-\eta_i|<\delta$ ，可证得：

$$\begin{aligned}&\left|\sum_{i=1}^nf(\xi_i)\Delta x_i-[F(b)-F(a)]\right|\\ =&\left|\sum_{i=1}^n[f(\xi_i)-f(\eta_i)]\Delta x_i\right|\\ \leq&\sum_{i=1}^n|f(\xi_i)-f(\eta_i)|\Delta x_i\\ <&\frac{\varepsilon}{b-a}\cdot\sum_{i=1}^n\Delta x_i=\varepsilon\end{aligned}$$

综上所述，当 $F(x)$ 是连续函数 $f(x)$ 在 $[a,b]$ 上的一个原函数时，有以下公式成立：

$$\int_a^bf(x)\mathrm{d}x=F(x)|_a^b=F(b)-F(a)$$

这便是牛顿-莱布尼茨公式（Newton-Leibniz formula） 的完整形式。

定积分换元积分法

若 $f(x)\in C[a,b]$ ，单值函数 $x=\varphi(t)$ ，满足：

1. $\varphi(t)\in C^1[\alpha,\beta]$ 且单调
2. 在 $[\alpha,\beta]$ 上 $a\leq\varphi(t)\leq b,\varphi(\alpha)=a,\varphi(\beta)=b$

则

$$\int_a^bf(x)\mathrm{d}x=\int_\alpha^\beta f[\varphi(t)]\varphi'(t)\mathrm{d}t$$

证明：

设 $F(x)$ 是 $f(x)$ 的一个原函数，则 $F[\varphi(t)]$ 是 $f[\varphi(t)]\varphi'(t)\mathrm{d}t$ 的原函数，因此

$$\begin{aligned}\int_a^bf(x)\mathrm{d}x=&F(b)-F(a)=F[\varphi(\beta)]-F[\varphi(\alpha)]\\ =&\int_\alpha^\beta f[\varphi(t)]\varphi'(t)\mathrm{d}t\end{aligned}$$

当区间换为 $[\beta,\alpha]$ 时，定理仍成立。
换元必换限，原函数中的变量不必代回。
令 $x=\varphi(t)$ ，换元公式反过来使用依然成立。

偶倍奇零：

设 $f(x)\in C[-a,a]$

1. 若 $f(x)$ 是偶函数，则 $\int_{-a}^af(x)\mathrm{d}x=2\int_0^af(x)\mathrm{d}x$
2. 若 $f(x)$ 是奇函数，则 $\int_{-a}^af(x)\mathrm{d}x=0$

周期函数积分：

设 $f(x)\in C(\mathbb R)$ ，且有一周期为 $T$ ，则 $\forall a\in\mathbb R$ ，有

$$\int_a^{a+T}f(x)\mathrm{d}x=\int_0^Tf(x)\mathrm{d}x$$

定积分分部积分法

设 $u(x),v(x)\in C^1[a,b]$ ，则

$$\int_a^bu(x)v'(x)\mathrm{d}x=u(x)v(x)\bigg|_a^b-\int_a^bu'(x)v(x)\mathrm{d}x$$

证明：

由

$$[u(x)v(x)]'=u'(x)v(x)+u(x)v'(x)$$

两边积分得：

$$u(x)v(x)\bigg|_a^b=\int_a^bu'(x)v(x)\mathrm{d}x+\int_a^bu(x)v'(x)\mathrm{d}x$$

所以可以移项得：

$$\int_a^bu(x)v'(x)\mathrm{d}x=u(x)v(x)\bigg|_a^b-\int_a^bu'(x)v(x)\mathrm{d}x$$

分部积分公式的推广：

若在 $[a,b]$ 上 $u(x),v(x)$ 有 $n+1$ 阶连续导函数，则有

$$\begin{aligned} \int_a^bu(x)v^{(n+1)}(x)\mathrm{d}x&=\left[u(x)v^{(n)}(x)-u'(x)v^{(n-1)}(x)+\cdots+(-1)^nu^{(n)}(x)v(x)\right]_a^b\\ &+(-1)^{n+1}\int_a^bu^{(n+1)}(x)v(x)\mathrm{d}x\\ &(n=1,2,\cdots) \end{aligned}$$

泰勒公式的积分型与柯西型余项

设函数 $f$ 在点 $x_0$ 的某邻域 $U(x_0)$ 上有 $n+1$ 阶连续导函数。
令 $x\in U(x_0)$，$u(t)=(x-t)^n$，$v(t)=f(t)$，$t\in[x_0,x]$，利用分布积分的推广公式可得：

$$\begin{aligned} &\quad\int_{x_0}^x(x-t)^nf^{n+1}(t)\mathrm{d}t\\ &=\left[(x-t)^nf^{(n)}(t)+n(x-t)^{n-1}f^{(n-1)}(t)+\cdots+n!f(t)\right]_{x_0}^x+\int_{x_0}^x0\cdot f(t)\mathrm{d}t\\ &=n!f(x)-n!\left[f(x_0)+f'(x_0)(x-x_0)+\cdots+\frac{f^{(n)}(x_0)}{n!}(x-x_0)^n\right] \end{aligned}$$

可以看到，这与泰勒公式的形式是类似的，由此推断出泰勒公式的 $n$ 阶余项可以表示为

$$R_n(x)=\frac{1}{n!}\int_{x_0}^xf^{(n+1)}(t)(x-t)^n\mathrm dt$$

这就是泰勒公式的积分型余项。

由于 $f^{(n+1)}(t)$ 连续，并且 $(x-t)^n$ 在 $[x_0,x]$ 上同号，由积分第一中值定理的推论可得：

$$\begin{aligned} R_n(x)&=\frac{1}{n!}f^{(n+1)}(\xi)\int_{x_0}^x(x-t)^n\mathrm dt\\ &=\frac{1}{(n+1)!}f^{(n+1)}(\xi)(x-x_0)^{n+1} \end{aligned}$$

这就转化为了我们熟悉的拉格朗日型余项。

将积分第一中值定理直接应用于上式，可得：

$$R_n(x)=\frac{1}{n!}f^{(n+1)}(\xi)(x-\xi)^n(x-x_0)$$

令 $\xi=x_0+\theta(x-x_0),\ 0\leq\theta\leq 1$，则

$$\begin{aligned} (x-\xi)^n(x-x_0)&=[x-x_0-\theta(x-x_0)]^n(x-x_0)\\ &=(1-\theta)^n(x-x_0)^{n+1} \end{aligned}$$

最终可将 $R_n(x)$ 改写为：

$$R_n(x)=\frac{1}{n!}f^{(n+1)}(x_0+\theta(x-x_0))(1-\theta)^n(x-x_0)^{n+1},\quad 0\leq\theta\leq 1$$

特别地，当 $x_0=0$ 时，又有

$$R_n(x)=\frac{1}{n!}f^{(n+1)}(\theta x)(1-\theta)^nx^{n+1},\quad 0\leq\theta\leq 1$$

以上两个公式称作泰勒公式的柯西型余项。

定积分的应用

求平面图形的面积

直角坐标方程表示的平面图形：

在平面直角坐标系中有两个 $y=f(x)$ 型连续函数的图像，垂直于x轴作两条直线，围成的面积叫作x型区域：

$$A=\{(x,y)|f_1(x)\leq y\leq f_2(x),x\in [a,b]\}$$

该区域面积的计算公式为：

$$\begin{aligned}S(A)&=\int_a^b(f_2(x)+M)\mathrm dx-\int_a^b(f_1(x)+M)\mathrm dx\\&=\int_a^b[f_2(x)-f_1(x)]\mathrm dx\end{aligned}$$

在平面直角坐标系中有两个 $x=g(y)$ 型连续函数的图像，垂直于y轴作两条直线，围成的面积叫作y型区域：

$$B=\{(x,y)|g_1(y)\leq x\leq g_2(y),y\in [c,d]\}$$

该区域面积的计算公式为：

$$S(B)=\int_c^d[g_2(y)-g_1(y)]\mathrm dy$$

若围成区域的边缘皆垂直于坐标轴或皆不垂直于坐标轴，则该区域既是x型区域也是y型区域，这时候从x型区域求法和y型区域求法挑选一个好用的方法求面积。

参数方程表示的平面图形：

设曲线由参数方程表示：

$$\left\{\begin{aligned}x=x(t)\\y=y(t)\end{aligned}\right.,t\in [\alpha,\beta]$$

其中 $y(t)$ 连续，$x(t)$ 连续可微。

该曲线所围成的区域面积计算公式为：

$$S(A)=\int_\alpha^\beta|y(t)x'(t)|\mathrm dt$$

极坐标表示的平面图形的面积：

设曲线 $C$ 的极坐标方程为 $r=r(\theta),\theta\in [\alpha,\beta]$。图形 $A$ 由曲线 $C$ 和两条射线 $\theta=\alpha$ 与 $\theta=\beta$ 围成。

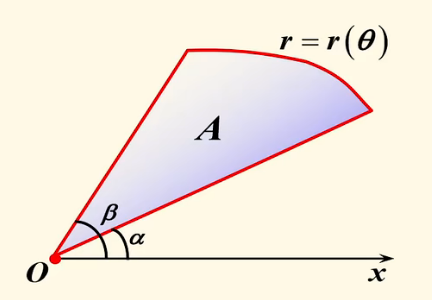
该区域的面积计算公式为：

$$S(A)=\frac{1}{2}\int_\alpha^\beta r^2(\theta)\mathrm d\theta$$

由横截面求体积

求不规则体体积：

$\Omega$ 为三维空间中一立体，它夹在垂直于 $x$ 轴的两平面 $x=a,x=b\ (a<b)$ 之间。

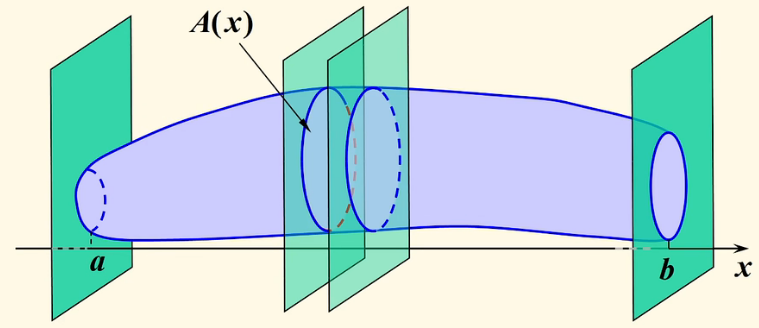
$\forall x\in[a,b]$，作垂直于 $x$ 轴的另一平面，将其截 $\Omega$ 得到的截面面积可以写成函数 $A(x)$，若 $A(x)$ 在 $[a,b]$ 上连续，则

$$V(\Omega)=\int_a^bA(x)\mathrm dx$$

例：求椭球体 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}+\dfrac{z^2}{c^2}=1$ 的体积。

以 $x$ 为自变量，将原式进行变形：

$$\begin{aligned} \dfrac{y^2}{b^2}+\dfrac{z^2}{c^2}&=1-\dfrac{x^2}{a^2}\\ \dfrac{y^2}{b^2(1-\dfrac{x^2}{a^2})}+\dfrac{z^2}{c^2(1-\dfrac{x^2}{a^2})}&=1 \end{aligned}$$

该式即为平面椭圆的标准表达式，由椭圆的面积公式 $S=\pi\cdot a\cdot b$ 可得：

$$\begin{aligned} A(x)&=\pi\cdot\sqrt{b^2(1-\dfrac{x^2}{a^2})}\cdot\sqrt{c^2(1-\dfrac{x^2}{a^2})}\\ &=\pi\cdot b\cdot c\cdot(1-\dfrac{x^2}{a^2}) \end{aligned}$$

对该函数进行积分即可得到椭球体的体积：

$$\begin{aligned} V&=\int_{-a}^a\pi bc(1-\dfrac{x^2}{a^2})\mathrm dx\\ &=\pi bc(x-\frac{x^3}{3a^2})\bigg|_{-a}^a\\ &=\frac{4}{3}\pi abc \end{aligned}$$

求旋转体体积：

设 $f$ 是 $[a,b]$ 上的连续函数，$\Omega$ 是由平面图形

$$A=\{(x,y)|0\leq|y|\leq|f(x)|,a\leq x\leq b\}$$

绕 $x$ 轴旋转一周所得的旋转体，则

$$A(x)=\pi f^2(x),x\in[a,b]$$

$$V=\pi\int_a^bf^2(x)\mathrm dx$$

如果所求旋转体是空心的圆环，则需要分别写出上半圆和下半圆的函数表达式 $f_1,f_2$，并且 $A(x)=\pi f_1^2(x)-\pi f_2^2(x)$.

类似地，可得绕 $y$ 轴旋转一周所得的旋转体体积为

$$V=\int_a^b2\pi xf(x)\mathrm dx$$

平面曲线的弧长

设平面曲线 $C$ 由以下参数方程表示：

$$x=x(t),y=y(t),t\in[\alpha,\beta]$$

如果 $x(t)$ 和 $y(t)$ 在 $[\alpha,\beta]$ 上连续可微，且 $x'(t)$ 与 $y'(t)$ 不同时为零，则称 $C$ 是一条光滑曲线。

对于光滑曲线 $C$，它的弧长是可求的，并且借助弧微分的概念，我们可以得到以下公式：

$$s=\int_\alpha^\beta\sqrt{[x'(t)]^2+[y'(t)]^2}\mathrm{d}t$$

若曲线 $C$ 由极坐标方程 $r=r(\theta),\theta\in[\alpha,\beta]$ 表示，则 $C$ 可看作：

$$x=r(\theta)\cos\theta,y=r(\theta)\sin\theta$$

同理可得弧长公式：

$$s=\int_\alpha^\beta\sqrt{[r(\theta)]^2+[r'(\theta)]^2}\mathrm{d}\theta$$

反常积分

定积分的积分区间都是有限的，并且被积函数都是有限的。但在实际应用和理论研究中，还会遇到一些在无限区间上定义的函数或有限区间上的无界函数，对它们也需要考虑类似于定积分的问题。因此，有必要对定积分的概念加以推广，使之能适用于上述两类函数。这种推广的积分，就称作广义积分或反常积分（Improper integral）。

无穷积分

设函数 $f$ 定义在 $[a,+\infty)$ 上，且在任何有限区间 $[a,u]$ 上可积，若存在极限

$$\lim_{u\to+\infty}\int_a^uf(x)\mathrm dx=J$$

则称此极限 $J$ 为函数 $f$ 在 $[a,+\infty)$ 上的无穷限反常积分，简称无穷积分，记作：

$$J=\int_a^{+\infty}f(x)\mathrm dx$$

并称 $\int_a^{+\infty}f(x)\mathrm dx$ 收敛；反之，若该极限不存在，则称 $\int_a^{+\infty}f(x)\mathrm dx$ 发散。

类似的，我们也可以写出如下定义：

$$\int_{-\infty}^bf(x)\mathrm dx=\lim_{u\to-\infty}\int_u^bf(x)\mathrm dx$$

$$\int_{-\infty}^{+\infty}f(x)\mathrm dx=\int_{-\infty}^af(x)\mathrm dx+\int_a^{+\infty}f(x)\mathrm dx$$

只有当 $\int_{-\infty}^af(x)\mathrm dx$ 和 $\int_a^{+\infty}f(x)\mathrm dx$ 同时收敛时，$\int_{-\infty}^{+\infty}f(x)\mathrm dx$ 才收敛。

无穷积分的牛顿-莱布尼茨公式：

$$\begin{aligned} \int_a^{+\infty}f(x)\mathrm dx&=F(x)\bigg|_a^{+\infty}\\ &=F(+\infty)-F(a)\\ &=\lim_{u\to+\infty}F(u)-F(a) \end{aligned}$$

无穷积分的性质：

性质1： 两个相同限的无穷积分可以线性组合：若 $\int_a^{+\infty}f_1(x)\mathrm dx$ 与 $\int_a^{+\infty}f_2(x)\mathrm dx$ 都收敛，$k_1,k_2$ 为任意常数，则

$$\int_a^{+\infty}(k_1f_1(x)+k_2f_2(x))\mathrm dx$$

也收敛，并且

$$\begin{aligned} \int_a^{+\infty}&(k_1f_1(x)+k_2f_2(x))\mathrm dx\\ &=k_1\int_a^{+\infty}f_1(x)\mathrm dx+k_2\int_a^{+\infty}f_2(x)\mathrm dx \end{aligned}$$

性质2： 对于同一可积函数在不同限上的无穷积分：$\int_a^{+\infty}f(x)\mathrm dx$ 和 $\int_b^{+\infty}f(x)\mathrm dx$，同时收敛或同时发散，并且

$$\int_a^{+\infty}f(x)\mathrm dx=\int_a^bf(x)\mathrm dx+\int_b^{+\infty}f(x)\mathrm dx$$

性质3： 设对于任何 $b>a$，$f(x)$ 在 $[a,b]$ 上可积，若无穷积分 $\int_a^{+\infty}|f(x)|\mathrm dx$ 收敛，则称无穷积分 $\int_a^{+\infty}f(x)\mathrm dx$ 为绝对收敛；若 $\int_a^{+\infty}f(x)\mathrm dx$ 收敛，而 $\int_a^{+\infty}|f(x)|\mathrm dx$ 发散，则称 $\int_a^{+\infty}f(x)\mathrm dx$ 为条件收敛。

若 $\int_a^{+\infty}f(x)\mathrm dx$ 绝对收敛，则此无穷积分收敛。

$$\left|\int_a^{+\infty}f(x)\mathrm dx\right|\leq \int_a^{+\infty}|f(x)|\mathrm dx$$

瑕积分

设函数 $f$ 定义在 $(a,b]$ 上，在 $a$ 的任意右邻域内无界，但在任何闭区间 $[u,b]$ 上有界且可积，若存在极限

$$\lim_{u\to a^+}\int_u^bf(x)\mathrm dx=J$$

则称此极限 $J$ 为函数 $f$ 在 $(a,b]$ 上的无界函数反常积分，简称瑕积分，记作：

$$J=\int_a^bf(x)\mathrm dx$$

并称 $\int_a^bf(x)\mathrm dx$ 收敛；反之，若该极限不存在，则称 $\int_a^bf(x)\mathrm dx$ 发散。

$a$ 被称作是该瑕积分的瑕点（Flaw），所谓瑕点，可以理解为使积分变得不完美的点。

类似的，我们也可以写出 $b$ 为瑕点时的瑕积分定义：

$$\int_a^bf(x)\mathrm dx=\lim_{u\to b^-}\int_a^uf(x)\mathrm dx$$

若 $f$ 的瑕点 $c\in(a,b)$，定义

$$\begin{aligned} \int_a^bf(x)\mathrm dx&=\int_a^cf(x)\mathrm dx+\int_c^bf(x)\mathrm dx\\ &=\lim_{u\to c^-}\int_a^uf(x)\mathrm dx+\lim_{v\to c^+}\int_v^bf(x)\mathrm dx \end{aligned}$$

只有当 $\int_a^cf(x)\mathrm dx$ 和 $\int_c^bf(x)\mathrm dx$ 同时收敛时，$\int_a^bf(x)\mathrm dx$ 才收敛。

瑕积分的牛顿-莱布尼茨公式：

以 $a$ 为瑕点：

$$\begin{aligned} \int_a^bf(x)\mathrm dx&=F(x)\bigg|_{a^+}^b\\ &=F(b)-F(a^+)\\ &=F(b)-\lim_{u\to{a^+}}F(u) \end{aligned}$$

瑕积分的性质：

性质1： 两个相同瑕点的瑕积分可以线性组合：若 $\int_a^bf_1(x)\mathrm dx$ 与 $\int_a^bf_2(x)\mathrm dx$ 的瑕点相同，$k_1,k_2$ 为任意常数，则

$$\int_a^b(k_1f_1(x)+k_2f_2(x))\mathrm dx$$

也收敛，并且

$$\begin{aligned} \int_a^b&(k_1f_1(x)+k_2f_2(x))\mathrm dx\\ &=k_1\int_a^bf_1(x)\mathrm dx+k_2\int_a^bf_2(x)\mathrm dx \end{aligned}$$

性质2： 对于同一可积函数相同瑕点在不同限上的瑕积分：设函数 $f$ 的瑕点为 $x=a$，若 $c\in(a,b)$，则 $\int_a^bf(x)\mathrm dx$ 和 $\int_a^cf(x)\mathrm dx$，同时收敛或同时发散，并且

$$\int_a^bf(x)\mathrm dx=\int_a^cf(x)\mathrm dx+\int_c^bf(x)\mathrm dx$$

性质3： 设函数 $f$ 的瑕点为 $x=a$，$f$ 在 $(a,b]$ 的任一闭区间 $[u,b]\ (u>a)$ 上可积，若瑕积分 $\int_a^b|f(x)|\mathrm dx$ 收敛，则称瑕积分 $\int_a^bf(x)\mathrm dx$ 为绝对收敛；若 $\int_a^bf(x)\mathrm dx$ 收敛，而 $\int_a^b|f(x)|\mathrm dx$ 发散，则称 $\int_a^bf(x)\mathrm dx$ 为条件收敛。

若 $\int_a^bf(x)\mathrm dx$ 绝对收敛，则此瑕积分收敛。

$$\left|\int_a^bf(x)\mathrm dx\right|\leq \int_a^b|f(x)|\mathrm dx$$

正项无穷积分的收敛判别法

定义判别法：

设定义在 $[a,+\infty)$ 上的非负函数 $f$ 在任何有限区间 $[a,u]$ 上可积，则 $\int_a^{+\infty}f(x)\mathrm dx$ 可积的充要条件是：$\exists M>0$，使

$$\forall u\in[a,+\infty),\ |\int_a^uf(x)\mathrm dx|\leq M$$

比较判别法：

设定义在 $[a,+\infty)$ 上的两个非负函数 $f,g$ 在任何有限区间 $[a,u]$ 上可积，且存在 $G>0$，满足

$$f(x)\leq g(x),\ x\in[G,+\infty)$$

• 当 $\int_a^{+\infty}g(x)\mathrm dx$ 收敛时，$\int_a^{+\infty}f(x)\mathrm dx$ 也收敛。
• 当 $\int_a^{+\infty}f(x)\mathrm dx$ 发散时，$\int_a^{+\infty}g(x)\mathrm dx$ 也发散。

比较判别法的极限形式：

设 $f(x),g(x)$ 在 $[a,+\infty)(a>0)$ 上非负连续，$g(x)>0$，并且

$$\lim_{x\to+\infty}\frac{f(x)}{g(x)}=l$$

• 若 $0<l<+\infty$，$\int_a^{+\infty}g(x)\mathrm dx$ 和 $\int_a^{+\infty}f(x)\mathrm dx$ 收敛性相同。
• 若 $l=0$，当 $\int_a^{+\infty}g(x)\mathrm dx$ 收敛时，$\int_a^{+\infty}f(x)\mathrm dx$ 也收敛。
• 若 $l=+\infty$，当 $\int_a^{+\infty}g(x)\mathrm dx$ 发散时，$\int_a^{+\infty}f(x)\mathrm dx$ 也发散。

在使用无穷积分的比较判别法时，常用 $f(x)=\dfrac{1}{x^p}\ (p>0)$ 作为比较大小的基准函数，它的无穷积分 $\displaystyle\int_1^{+\infty}\frac{1}{x^p}\mathrm dx$ 的收敛性很容易可以证得：

当 $p=1$ 时，

$$\int_1^{+\infty}\frac{\mathrm dx}{x}=\lim_{1\to+\infty}\int_1^b\frac{\mathrm dx}{x}=\lim_{1\to+\infty}\ln b=+\infty$$

故该无穷积分发散。

当 $p\neq 1$ 时，

$$\int_1^{+\infty}\frac{\mathrm dx}{x^p}=\frac{x^{1-p}}{1-p}\bigg|_1^{+\infty}=\left\{\begin{aligned}&+\infty,\ &p<1\\&\frac{1}{p-1},\ &p>1\end{aligned}\right.$$

综上所述，当 $p\leq 1$ 时，该无穷积分发散；当 $p>1$，该无穷积分收敛。

由基准函数得到的推论：设 $f(x)$ 在 $[a,+\infty)(a>0)$ 上非负连续，且

$$\lim_{x\to+\infty}x^pf(x)=l$$

• 当 $0\leq l<+\infty$ 且 $p>1$ 时，$\int_a^{+\infty}f(x)\mathrm dx$ 收敛。
• 当 $0<l\leq+\infty$ 且 $p\leq 1$ 时，$\int_a^{+\infty}f(x)\mathrm dx$ 发散。

正项瑕积分的收敛判别法

比较判别法：

设 $f(x),g(x)\in C[a,b)$，$b$ 是它们的瑕点，并且满足

$$0\leq f(x)\leq g(x),\ x\in[c,b)\subset[a,b)$$

• 当 $\int_a^bg(x)\mathrm dx$ 收敛时，$\int_a^bf(x)\mathrm dx$ 也收敛。
• 当 $\int_a^bf(x)\mathrm dx$ 发散时，$\int_a^bg(x)\mathrm dx$ 也发散。

比较判别法的极限形式：

设 $f(x),g(x)$ 在 $[a,b)(a>0)$ 上非负连续，$b$ 是它们的瑕点，$g(x)>0$，并且

$$\lim_{x\to b^-}\frac{f(x)}{g(x)}=l$$

• 若 $0<l<+\infty$，$\int_a^bg(x)\mathrm dx$ 和 $\int_a^bf(x)\mathrm dx$ 收敛性相同。
• 若 $l=0$，当 $\int_a^bg(x)\mathrm dx$ 收敛时，$\int_a^bf(x)\mathrm dx$ 也收敛。
• 若 $l=+\infty$，当 $\int_a^bg(x)\mathrm dx$ 发散时，$\int_a^bf(x)\mathrm dx$ 也发散。

在使用瑕积分的比较判别法时，常用 $f(x)=\dfrac{1}{(b-x)^p}$ 或 $f(x)=\dfrac{1}{(x-a)^p}\ (a<b,p>0)$ 作为比较大小的基准函数。瑕积分 $\displaystyle\int_a^b\dfrac{\mathrm dx}{(b-x)^p}$ 的收敛性很容易可以证得：

令 $x=b$ 为瑕点，

当 $p=1$ 时，

$$\int_a^b\dfrac{\mathrm dx}{b-x}=-\ln(b-x)\bigg|_a^b=+\infty$$

故该瑕积分发散。

当 $p\neq 1$ 时，

$$\int_a^b\dfrac{\mathrm dx}{(b-x)^p}=-\frac{1}{1-p}(b-x)^{1-p}\bigg|_a^b=\left\{\begin{aligned}&\frac{1}{1-p}(b-a)^{1-p},\ &p<1\\&+\infty,\ &p>1\end{aligned}\right.$$

综上所述，积分 $\displaystyle\int_a^b\dfrac{\mathrm dx}{(b-x)^p}$ 当 $0<p<1$ 时收敛，当 $p\geq1$ 时发散。

同理可得，积分 $\displaystyle\int_a^b\dfrac{\mathrm dx}{(x-a)^p}$ 当 $0<p<1$ 时收敛，当 $p\geq 1$ 时发散。

由基准函数得到的推论：

若 $a$ 是瑕点，取 $g(x)=\dfrac{1}{(x-a)^p}$，并且

$$\lim_{x\to a^+}(x-a)^pf(x)=l$$

若 $b$ 是瑕点，取 $g(x)=\dfrac{1}{(b-x)^p}$，并且

$$\lim_{x\to b^-}(b-x)^pf(x)=l$$

• 当 $0\leq l<+\infty$ 且 $0<p<1$ 时，$\int_a^bf(x)\mathrm dx$ 收敛。
• 当 $0<l\leq+\infty$ 且 $p\geq 1$ 时，$\int_a^bf(x)\mathrm dx$ 发散。