数学分析初步（一）：数与极限

实数

有理数（Rational number）的定义：任何一个有理数都可以用 $\frac{p}{q}$ 表示，其中 $p$ 和 $q$ 都是整数并且 $q\neq0$ ，任何一个有理数都可以用无限循环小数表示：

$$x=a_0a_1a_2\cdots a_n=a_0a_1a_2\cdots a_{n-1}\dot9$$

其中0是特例，对其有特别规定：

$$0=0.00000\cdots$$

无理数（Irrational number）的定义：无法用以上形式表示，并且只能表示为无限不循环小数。

由此有理数和无理数都可以用无限小数的形式表示，比较实数的大小也就是将小数的各位依次进行比较。

正数的 $n$ 位不足近似 $x_n$ ：将第 $n$ 位小数点后的所有数字直接舍去。
正数的 $n$ 位过剩近似 $\overline{x_n}$ ：将第 $n$ 位小数点后的所有数字直接舍去并向前进一位。

负数的近似方法与正数完全相反。

命题：当 $x>y$ 时，$\exists$ 非负整数 $n$ ， 使 $x_n>\overline{y_n}$

实数集

实数集 $\mathbb{R}=\{x|x是实数\}$ 的性质：

1. 四则运算的封闭性：实数经过四则运算后依旧是实数
2. 有序性：实数的大小可以被排序
3. 传递性：实数的大小关系可以被传递
4. 阿基米德性：$a,b\in \mathbb{R}\quad b>a>0\quad \exists正整数n\quad 使na>b$
5. 稠密性：任意两个不相等的数之间一定存在实数
6. 实数集和数轴上的点一一对应

邻域

$a\in\mathbb{R}\quad\delta>0\quad|x-a|<\delta$ 的全体 $x$ 称为 $a$ 的 $\delta$ 邻域（Neighbourhood），记作 $U(a,\delta)$

不包含 $a$ 本身的邻域称作去心邻域，记作 $\mathring{U}(a,\delta)$ ， $\mathring{U}(a,\delta)=\{x|0<|x-a|<\delta\}$

右邻域 $U_+(a,\delta)=[a,a+\delta)$ ，左邻域 $U_-(a,\delta)=(a-\delta,a]$

无穷邻域 $U(\infty)=\{x||x|>M\}$ ， $M$ 是一个充分大的实数

确界原理

$S$ 是 $\mathbb{R}$ 中的数集

$\exists M$ 使一切 $x\in S\quad x\leq M$ ，则 $S$ 的上界为 $M$
$\exists L$ 使一切 $x\in S\quad x\geq L$ ，则 $S$ 的下界为 $L$

既有上界又有下界，则 $S$ 为有界集，否则为无界集。

上确界表示最小的上界，下确界表示最大的下界。

• 对一切 $x\in S\quad x\leq\eta$ ，则 $\eta$ 是 $S$ 的上界。
  $\forall\alpha<\eta\quad\exists x_0\in S$ 使 $x_0>\alpha$ 即 $\eta$ 是 $S$ 的上确界，记作 $\sup S$ 。

• 同理，对一切 $x\in S\quad x\geq\xi$ ，则 $\xi$ 是 $S$ 的下界。
  $\forall\beta>\xi\quad\exists x_0\in S$ 使 $x_0>\beta$ 即 $\xi$ 是 $S$ 的下确界，记作 $\inf S$ 。

函数

函数的定义：两个实数集 $D,M$ 和规则 $f$，$\forall x\in D$，有唯一的 $y\in M$ 与之对应，写作映射 $f:D\rightarrow M,x\rightarrow y$。

$$f(D)=\{y|y=f(x),x\in D\}\subset M$$

使得函数能自然成立的定义域就被称为函数的存在域。

函数的单值对应关系：$a$ 被称为原像，$f(a)$ 被称为像。

函数的复合和四则运算

复合函数的定义：
$y=f(u)\quad u\in D\qquad u=g(x)\quad x\in E\\ y=f(g(x))\quad x\in E^*\\ E^*=\{x|g(x)\in D\}\cap E\neq\emptyset$

复合函数 $y=f(g(x))$ 可以记作 $(f\circ g)(x)$

已知 $f(x)$ 定义域为 $x\in D_1$ ， $g(x)$ 定义域为 $x\in D_2$
在定义域 $D=D_1\cap D_2\neq0$ 上，有加减法定义 $f(x)\pm g(x)$ 和乘法定义 $f(x)\cdot g(x)$
在定义域 $D^*=\{x|g(x)\neq0,x\in D_2\}\cap D_1\neq\emptyset$ 上，有除法定义 $\frac{f(x)}{g(x)}$

反函数

对于函数 $y=f(x)\quad x\in D$ ，有其逆映射 $f^{-1}:f(D)\rightarrow D$ ，只有在原映射关系是一一映射的情况下才有逆映射， $y=f^{-1}(x)$ 就被称作反函数。

反函数满足 $f^{-1}(f(x))=x\quad x\in D\qquad f(f^{-1}(y))=y\quad y\in f(D)$ ，原函数和反函数的图像关于 $y=x$ 对称。

原函数和反函数的定义域，值域相互交换。

反三角函数：

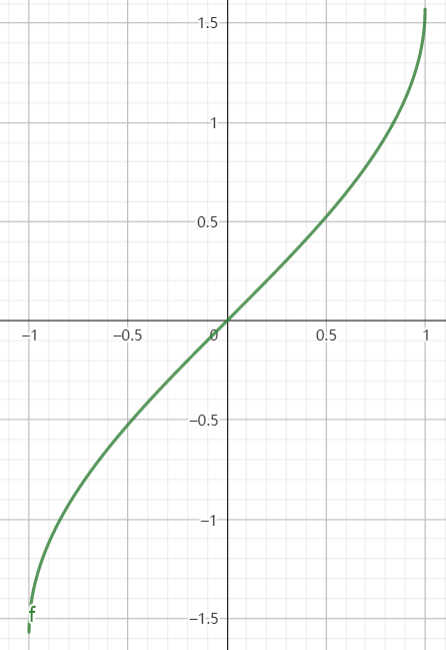
反正弦函数：

$$y=\arcsin x\quad x\in[-1,1]\quad y\in[-\frac{\pi}{2},\frac{\pi}{2}]$$

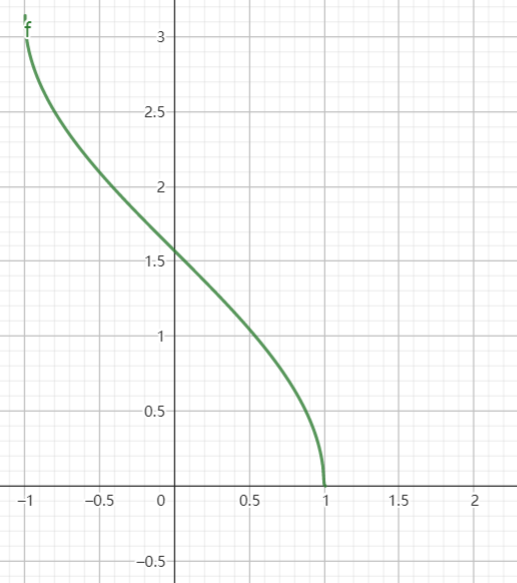
反余弦函数：

$$y=\arccos x\quad x\in[-1,1]\quad y\in[0,\pi]$$

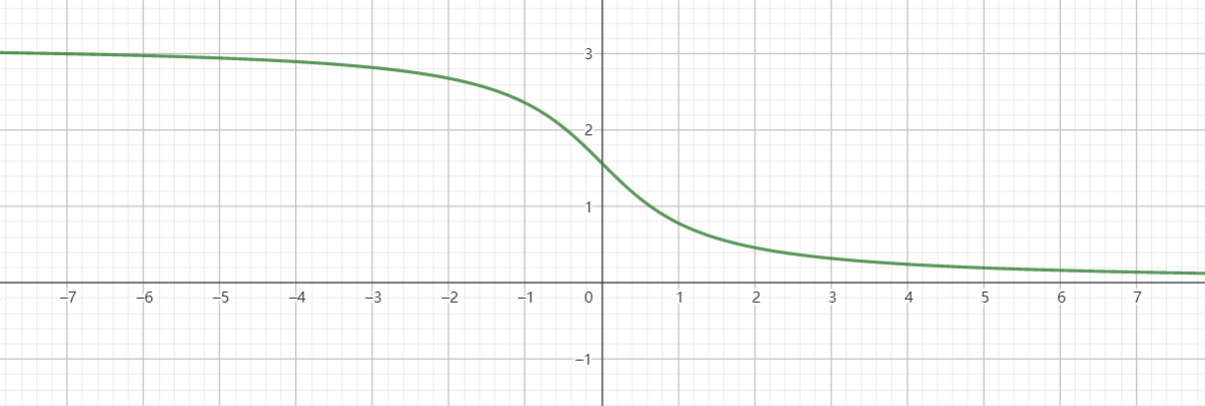
反正切函数：

$$y=\arctan x\quad x\in\mathbb{R}\quad y\in(-\frac{\pi}{2},\frac{\pi}{2})$$

反余切函数：

$$y=\mathrm{arccot} x\quad x\in\mathbb{R}\quad y\in(0,\pi)$$

初等函数

基本初等函数：

1. $y=C$ （ $C$ 是常数）
2. $y=x^\alpha$ （ $\alpha$ 是实数）
3. $y=a^x$ （ $a>0\quad a\neq1$）
4. 三角函数
5. 反三角函数

特别的，对于 $a^x$ 有以下规定：

$$a^x=\left\{\begin{aligned} &\sup r<x\ \{a^r|r为有理数\},&a>1\\ &\inf r<x\ \{a^r|r为有理数\},&0<a<1 \end{aligned}\right.$$

由基本初等函数经过有限次四则运算和复合得到的函数依旧是初等函数，例如分段函数 $y=|x|=\sqrt{x^2}$ 也是初等函数。

函数的性质

有界性：

上界：$\exists M\quad f(x)\leq M$
下界：$\exists L\quad f(x)\geq L$

函数有界： $\exists M\quad\forall x\in D\quad|f(x)|\leq M$

函数无界：

• 无上界： $\forall M\quad\exists x\in D\quad f(x)>M$
• 无下界： $\forall L\quad\exists x\in D\quad f(x)<L$
• 无界： $\forall M\quad\exists x\in D\quad|f(x)|>M$

单调性：

$x_1,x_2\in D\quad x_1<x_2$

$f(x_1)\leq(x_2)\quad$ 增函数
$f(x_1)<(x_2)\quad$ 严格增函数
$f(x_1)\geq(x_2)\quad$ 减函数
$f(x_1)>(x_2)\quad$ 严格减函数

定理：若 $y=f(x)$ 严格增（减），则 $f$ 必有 $f^{-1}$ ，且 $f^{-1}$ 在 $f(D)$ 上严格增（减）。

证明：

令 $x_1\neq x\quad f$ 严增
$x_1<x\quad f(x_1)<f(x)\\x_1>x\quad f(x_1)>f(x)$

必有 $f^{-1}$ ，使得 $y_1<y_2\in f(D)\\f(x_1)=y_1\quad f(x_2)=y_2$

由 $f$ 严增，得 $x_1<x_2$
可证得 $x_1=f^{-1}(y_1)<x_2=f^{-1}(y_2)$

奇偶性：

奇函数： $f(-x)=-f(x)$
偶函数： $f(-x)=f(x)$

奇函数 $\pm$ 奇函数 $=$ 奇函数
偶函数 $\pm$ 偶函数 $=$ 偶函数

奇函数 $\cdot$ 奇函数 $=$ 偶函数
偶函数 $\cdot$ 偶函数 $=$ 偶函数

奇函数 / 奇函数 $=$ 偶函数
偶函数 / 偶函数 $=$ 偶函数

周期性：

周期的定义： $\sigma>0\quad x\in D\quad x\pm\sigma\in D$

若 $f(x\pm\sigma)=f(x)$ ，则将 $\sigma$ 称为函数的周期，并且 $n\sigma$ 也是函数的周期。

数列极限

数列极限的定义：

$\{a_n\}$ ， $a$ 是定数， $\forall\varepsilon>0$ ， $\exists$ 正整数 $N$ ， 使 $n>N$ 时， $|a_n-a|<\varepsilon$ ，则称 $\{a_n\}$ 收敛于 $a$ ，记作 $\lim\limits_{n\rightarrow+\infty}a_n=a$ ， $a_n\rightarrow a(n\rightarrow+\infty)$ 。

例： 证明 $\lim\limits_{n\rightarrow+\infty}\frac{1}{n}=0$ 。

分析：

$$|\frac{1}{n}-0|<\varepsilon\\ \frac{1}{n}<\varepsilon\\ n>\frac{1}{\varepsilon}$$

证： $\forall\varepsilon>0\qquad\exists N=[\frac{1}{\varepsilon}]+1$

$$n>N=[\frac{1}{\varepsilon}]+1>\frac{1}{\varepsilon}\\ \frac{1}{n}<\varepsilon\\ |\frac{1}{n}-0|<\varepsilon$$

邻域法判定数列极限是否存在：

1. $\forall\varepsilon>0$ ，若 $U(a,\varepsilon)$ 外只有有限项，则数列以 $a$ 为极限。
2. $\exists\varepsilon_0>0$ ，若 $U(a,\varepsilon_0)$ 外有无穷项，则数列不以 $a$ 为极限。
3. $\exists\varepsilon_0>0$ ，若 $\forall a$ ，在 $U(a,\varepsilon_0)$ 外都有无穷项，则数列没有极限，即数列发散。

推论： 存在数列 $\{a_n\}$ ，数列 $\{b_n\}$ 是在 $\{a_n\}$ 的基础上增加，减少或改变有限项，则两数列同时收敛或发散，收敛时拥有相同的极限。

证：若 $\lim\limits_{n\rightarrow\infty}a_n=a$ ，则 $\forall\varepsilon>0$ ，在 $\{a_n\}$ 在 $U(a,\varepsilon)$ 外只有有限项，并且 $\{a_n\}$ 和 $\{b_n\}$ 仅在有限项上有差别，因此 $\{b_n\}$ 在 $U(a,\varepsilon)$ 外也只有有限项。

若 $\{a_n\}$ 发散，假设 $\{b_n\}$ 收敛，并且 $\{a_n\}$ 和 $\{b_n\}$ 仅在有限项上有差别，因此 $\{a_n\}$ 也应收敛，产生矛盾，所以 $\{b_n\}$ 应该发散。

无穷大与无穷小

无穷小数列：

若 $\lim\limits_{n\rightarrow\infty}a_n=0$ ，则 $\{a_n\}$ 被称为无穷小数列。

推论： 若 $\lim\limits_{n\rightarrow\infty}a_n=a$ ，则 $\{a_n-a\}$ 是无穷小数列。

证： $\forall\varepsilon>0$ ， $\exists N$ ，$n>N$ ， $|a_n-a|<\varepsilon$ ，即 $|(a_n-a)-0|<\varepsilon$ ，所以 $\lim\limits_{n\rightarrow\infty}(a_n-a)=0$ 。

无穷大数列：

若对于 $\{a_n\}$ ， $\forall M>0$ ， $\exists N$ ，使得 $n>N$ 时， $|a_n|>M$ ，则 $\lim\limits_{n\rightarrow\infty}a_n=\infty$ ，称 $\{a_n\}$ 发散与无穷大，是无穷大数列。

1. 正无穷大： $\forall M>0$ ， $\exists N$ ，使得 $n>N$ 时， $a_n>M$ ，则 $\lim\limits_{n\rightarrow\infty}a_n=+\infty$
2. 负无穷大： $\forall M>0$ ， $\exists N$ ，使得 $n>N$ 时， $a_n<-M$ ，则 $\lim\limits_{n\rightarrow\infty}a_n=-\infty$

无界不一定无穷大，但无穷大一定无界。

收敛数列性质

极限的唯一性：

• 若 $\{a_n\}$ 收敛，则它只有一个极限。

证： $\lim\limits_{n\rightarrow\infty}a_n=a$ ，设 $b\neq a$ ，令 $\varepsilon_0=\frac{|a-b|}{2}$ ，因为在 $U(a,\varepsilon_0)$ 外只有有限项，所以在 $U(a,\varepsilon_0)$ 上也只有有限项，所以 $b$ 必然不是 $\{a_n\}$ 的极限。

有界性：

• 若 $\{a_n\}$ 收敛，则它一定有界。

证： $\lim\limits_{n\rightarrow\infty}a_n=a$ ， $\exists N$ ， $n>N$ ， $|a_n-a|<\varepsilon$ ，则 $a-\varepsilon<a_n<a+\varepsilon$
其必有上界 $M=\max\{|a_1|\cdots |a_N|,|a-\varepsilon|,|a+\varepsilon|\}$

保号性：

1. $\lim\limits_{n\rightarrow\infty}a_n=a>0$ ， $\forall a'\in[0,a)$ ， $\exists N$ ， $n>N$ ， 使得 $a_n>a'$ 。
2. $\lim\limits_{n\rightarrow\infty}a_n=a<0$ ， $\forall a'\in(a,0]$ ， $\exists N$ ， $n>N$ ， 使得 $a_n<a'$ 。

证：当 $a>0$ 时，令 $\varepsilon=a-a'$ ， $\exists N$ ， $n>N$ ，则 $a_n>a-\varepsilon=a'$ ，
当 $a<0$ 时，证明方法类似。

推论： $\lim\limits_{n\rightarrow\infty}a_n=a$ ， $\lim\limits_{n\rightarrow\infty}b_n=b$ ，且 $a<b$ ， $\exists N$ ， $n>N$ ，有 $a_n<b_n$ 。

证：令 $\varepsilon=\frac{b-a}{2}$ ，
$\exists N_1$ ， $n>N_1$ ，使 $a_n<\frac{a+b}{2}$ ；
$\exists N_2$ ， $n>N_2$ ，使 $b_n>\frac{a+b}{2}$ 。
则取 $N=\max\{N_1,N_2\}$ ， $a_n<b_n$ 。

保不等式性：

• $\{a_n\},\{b_n\}$ 收敛，若 $\exists N_0$ ， $n>N_0$ ，使 $a_n\leq b_n$ ，则 $\lim\limits_{n\rightarrow\infty}a_n\leq\lim\limits_{n\rightarrow\infty}b_n$ 。

证： $\lim\limits_{n\rightarrow\infty}a_n=a$ ， $\lim\limits_{n\rightarrow\infty}b_n=b$ ， $\forall\varepsilon>0$
$\exists N_1$ ， $n>N_1$ ，使 $a-\varepsilon<a_n$ ；
$\exists N_2$ ， $n>N_2$ ，使 $b_n<b+\varepsilon$
取 $N=\max\{N_0,N_1,N_2\}$ ，则 $a-\varepsilon<a_n\leq b_n<b+\varepsilon$ ，可得 $a<b+2\varepsilon$ ，
即 $a\leq b$ ，所以 $\lim\limits_{n\rightarrow\infty}a_n\leq\lim\limits_{n\rightarrow\infty}b_n$ 。

在保不等号性中，即使严格 $a_n<b_n$ ，极限间的关系依旧只能是 $\lim_{n\rightarrow\infty}a_n\leq\lim_{n\rightarrow\infty}b_n$ 。

迫敛性（夹逼定理Squeeze theorem）：

• 令 $\lim\limits_{n\rightarrow\infty}a_n=\lim\limits_{n\rightarrow\infty}b_n=a$，若存在 $a_n\leq c_n\leq b_n$，则 $\exists N_0$， $n>N_0$ 时， $\{c_n\}$ 收敛，且 $\lim\limits_{n\rightarrow\infty}c_n=a$ 。

证： $\forall\varepsilon>0$
$\exists N_1$ ， $n>N_1$ ，使 $a-\varepsilon<a_n$
$\exists N_2$ ， $n>N_2$ ，使 $b_n<a+\varepsilon$
取 $N=\max\{N_0,N_1,N_2\}$ ，则 $a-\varepsilon<a_n\leq c_n\leq b_n<a+\varepsilon$

可得 $a-\varepsilon<c_n<a+\varepsilon$ ，即 $|c_n-a|<\varepsilon$ ，所以 $\lim\limits_{n\rightarrow\infty}c_n=a$ 。

极限的四则运算：

若 $\{a_n\},\{b_n\}$ 均收敛，则可以进行极限的四则运算。

1. $\lim a_n\pm\lim b_n=\lim(a_n\pm b_n)$
2. $\lim a_n\cdot\lim b_n=\lim(a_n\cdot b_n)$
3. $\frac{\lim a_n}{\lim b_n}=\lim\frac{a_n}{b_n}\quad(\lim b_n\neq 0,b_n\neq 0)$

在使用上述公式拆分单个数列极限时，要注意拆分出的数列是否收敛。

子列

现有一数列 $\{a_n\}$ ，而 $\{n_k\}$ 是 $\mathbb{N_+}$ 的无限子集 $(n_k\geq k)$ ，构建一个新的数列 $\{a_{n_1},a_{n_2},\cdots ,a_{n_k}\}$ ，这个数列就称为 $\{a_n\}$ 的子列。 $\{a_n\}$ 本身也是它自己的子列。

$$\{a_n\} 收敛 \iff \{a_n\} 的任何子列都收敛$$

证明：

充分性：由于 $\{a_n\}$ 也是它自身的子列，所以当任何子列都收敛时，它自身收敛。

必要性：
$\{a_n\}$ 收敛， $\forall\varepsilon>0\quad N>0\quad k>N$
由于 $|a_k-a|<\varepsilon$ ， $n_k\geq k$
所以 $|a_{n_k}-a|<\varepsilon$
可证得 $\{a_{n_k}\}$ 收敛

使用子列证明数列发散：

1. 一个子列发散
2. 两个子列都收敛，但极限不相等

推论： 奇数子列和偶数子列都收敛，则该数列收敛。

$$\lim_{n\rightarrow\infty}a_n=A\iff\lim_{n\rightarrow\infty}a_{2n-1}=\lim_{n\rightarrow\infty}a_{2n}=A$$

数列极限存在定理

单调有界定理：

• 在实数系中，有界的单调数列必有极限。

证：设 $\{a_n\}$ 有上界且为递增数列，令 $a=\sup\{a_n\}$

$\forall\varepsilon>0\quad N>0$ ，则 $a-\varepsilon<a_N$
又因为 $\{a_n\}$ 单增，所以当 $n>N$ 时， $a_n\geq a_N>a-\varepsilon$

因为 $a$ 是 $\{a_n\}$ 的上界，所以 $a_n\leq a<a+\varepsilon$

综上所述， $a-\varepsilon<a_n<a+\varepsilon$ ，即该数列 $\{a_n\}$ 拥有极限。
其余情况可以用类似的方法证明。

致密性：

• 任何有界数列必有收敛的子列。

证：设 $a$ 是上确界， $\forall\varepsilon>0$

$\exists x\in S\quad x>a-\varepsilon$
$a\notin S\quad k<a$

取 $\varepsilon_1=1\quad\exists x_1\in S\quad a-\varepsilon_1<x_1<a$
$\varepsilon_2=\min\{\frac{1}{2},a-x_1\}\quad x_2>x_1\quad x_1< a-\varepsilon_2<x_2$
$\cdots$
$\varepsilon_n=\min{\frac{1}{n},a-x_{n-1}}\quad a-\varepsilon<x_n<a<a+\varepsilon_n\quad|x_n-a|<\varepsilon_n\leq\frac{1}{n}$

可证得当 $S$ 为有界数集时，若 $\sup S=a\notin S$ ，存在严格增 $\{x_n\}\subset S$ 。
同理可得，当 $S$ 为有界数集时，若 $\inf S=a\notin S$ ，存在严格减 $\{x_n\}\subset S$ 。

由单调有界原理得， $\{x_n\}$ 为收敛子列。

柯西收敛准则：

• $\{a_n\}$ 收敛 $\iff$ $\forall\varepsilon>0\quad\exists N$ ，对任何 $n,m>N$ ，有 $|a_n-a_m|<\varepsilon$

柯西收敛准则可以在不需要知道数列极限的情况下，证明数列收敛。

证明：

必要性：

$\lim\limits_{n\rightarrow\infty}a_n=A\quad\forall\varepsilon>0\quad\exists N\quad n,m>N$
此时 $|a_m-A|<\frac{\varepsilon}{2}\quad|a_n-A|<\frac{\varepsilon}{2}$
因此 $|a_n-a_m|=|a_n-A-(a_m-A)|<|a_n-A|+|a_m-A|<\varepsilon$

充分性：

令 $\varepsilon_0=1\quad\exists N_0\quad n>N_0$ 时，有 $|a_n-a_{N_0+1}|<1$
取 $M=\max\{|a_1|,|a_2|,\cdots ,|a_{N_0}|,|a_{N_0+1}|+1\}$ ，则有 $|a_n|<M$ ，可证得 $\{a_n\}$ 有界。

由致密性可得一子列使 $\lim\limits_{n\rightarrow+\infty}a_{n_k}=\xi$
$\forall\varepsilon>0\quad\exists N\quad n>N$ 时， $|a_n-a_m|<\frac{\varepsilon}{2}$
取 $a_m=a_{n_k}$ ，因为 $|a_n-\xi|\leq\frac{\varepsilon}{2}<\varepsilon$ ，可证得 $|a_n-a_m|<\varepsilon$ 。

函数极限

函数极限的定义：

$x\rightarrow\infty$ 型：

$f(x)$ 在 $[a,+\infty)$ 上有定义， $A$ 是定数， $\forall\varepsilon>0$ ， $\exists M(M\geq a)$ ， 使 $x>M$ 时， $|f(x)-A|<\varepsilon$ ，则称 $A$ 为 $f(x)$ 在 $x\rightarrow+\infty$ 的极限，记作 $\lim\limits_{x\rightarrow+\infty}f(x)=A$ 。

$x\rightarrow x_0$ 型：

$f(x)$ 在 $\mathring U(x_0,\delta')$ 上有定义， $A$ 是定数， $\forall\varepsilon>0$ ， $\exists\delta(\delta<\delta')$ ， 使 $0<|x-x_0|<\delta$ 时， $|f(x)-A|<\varepsilon$ ，则称 $A$ 为 $f(x)$ 在 $x\rightarrow x_0$ 的极限，记作 $\lim\limits_{x\rightarrow x_0}f(x)=A$ 。

单侧极限：

$f(x)$ 在 $\mathring U_+(x_0,\delta')$ 上有定义， $A$ 是定数， $\forall\varepsilon>0$ ， $\exists\delta(0<\delta<\delta')$ ， 使 $x_0<x<x_0+\delta$ 时， $|f(x)-A|<\varepsilon$ ，则称 $A$ 为 $f(x)$ 在 $x_0$ 处的右极限，记作 $\lim\limits_{x\rightarrow x_0^+}f(x)=A$ 。

同理可得 $f(x)$ 在 $x_0$ 处的左极限的定义，记作 $\lim\limits_{x\rightarrow x_0^-}f(x)=A$ 。

极限与两侧极限的关系：

$$\lim_{x\rightarrow x_0}f(x)=A\iff\lim_{x\rightarrow x_0^+}f(x)=\lim_{x\rightarrow x_0^-}f(x)=A$$

非正常极限：

$f(x)$ 在 $\mathring U(x_0,\delta')$ 上有定义， $\forall G>0$ ， $\exists\delta(0<\delta<\delta')$ ， 使 $x\in\mathring U(x_0,\delta)$ 时， $|f(x)|>G$ ，则称 $f(x)$ 在 $x\rightarrow x_0$ 时趋于无穷，记作 $\lim\limits_{x\rightarrow x_0}f(x)=\infty$ ，它是一种非正常极限，此时通常认为 $f(x)$ 的极限不存在。

函数极限的6种因变量变化过程：

1. $x\rightarrow\infty$
2. $x\rightarrow+\infty$
3. $x\rightarrow-\infty$
4. $x\rightarrow x_0$
5. $x\rightarrow+x_0$
6. $x\rightarrow-x_0$

函数极限性质

极限的唯一性：

• 若 $\lim f(x)=A$ ，则 $A$ 的值是唯一的。

局部有界性：

• 若 $\lim\limits_{x\rightarrow x_0}f(x)$ 存在，则 $f(x)$ 在 $\mathring U(x_0)$ 上有界。

局部保号性：

1. 若 $\lim\limits_{x\rightarrow x_0}f(x)=A>0$ ，则对任何 $0<r<A$ ， 存在 $x\in\mathring U(x_0)$ ，使得 $f(x)>r>0$ 。
2. 若 $\lim\limits_{x\rightarrow x_0}f(x)=A<0$ ，则对任何 $A<r<0$ ， 存在 $x\in\mathring U(x_0)$ ，使得 $0<r<f(x)$ 。

保不等式性：

• 若 $f(x)\leq g(x)$ ，则 $\lim f(x)\leq\lim g(x)$

迫敛性：

• $\lim f(x)=\lim g(x)=A$ ，若 $f(x)\leq h(x)\leq g(x)$ ，则 $\lim h(x)=A$

极限的四则运算：

若 $\lim f(x),\lim g(x)$ 都存在，则可以进行极限的四则运算。

1. $\lim f(x)\pm\lim g(x)=\lim(f(x)\pm g(x))$
2. $\lim f(x)\cdot\lim g(x)=\lim(a_n\cdot g(x))$
3. $\frac{\lim f(x)}{\lim g(x)}=\lim\frac{f(x)}{g(x)}\quad(\lim g(x)\neq 0,g(x)\neq 0)$

函数极限存在定理

单调有界定理：

• 若 $f$ 定义在 $\mathring U_+$ 上单调有界，则 $\lim\limits_{x\rightarrow x_0^+}f(x)$ 存在。

海涅定理（归结原则）：

• $f$ 在 $\mathring U(x_0,\delta')$ 上有定义， $\lim\limits_{x\rightarrow x_0}f(x)$ 存在的充要条件是任何含于 $\mathring U(x_0,\delta')$ 以 $x_0$ 为极限的数列 $\{x_n\}$ ，它的极限 $\lim\limits_{x\rightarrow\infty}f(x_n)$ 都存在且相等。

海涅定理是将函数极限和数列极限联系在一起的一个重要的桥梁。

$\lim\limits_{x\rightarrow x_0}f(x)=A\iff$ 任何 $x_n\rightarrow x_0(n\rightarrow\infty)$ ，都有 $\lim\limits_{x\rightarrow\infty}f(x_n)=A$
找到一个 $x_n\rightarrow x_0$ ，若 $\lim\limits_{x\rightarrow\infty}f(x_n)$ 不存在，则函数极限不存在。
找到两个 $x_n,x_n'\rightarrow x_0$ ，若 $\lim\limits_{x\rightarrow\infty}f(x_n)\neq\lim\limits_{x\rightarrow\infty}f(x_n')$ ，则函数极限不存在。

单侧极限海涅定理：

1. $f$ 在 $\mathring U_+(x_0)$ 上有定义， $\lim\limits_{x\rightarrow x_0^+}f(x)=A$ 的充分必要条件是以 $x_0$ 为极限的递减数列 $\{x_n\}\in\mathring U_+(x_0)$ ，它的极限 $\lim\limits_{x\rightarrow\infty}=A$ 。
2. $f$ 在 $\mathring U_-(x_0)$ 上有定义， $\lim\limits_{x\rightarrow x_0^-}f(x)=A$ 的充分必要条件是以 $x_0$ 为极限的递增数列 $\{x_n\}\in\mathring U_-(x_0)$ ，它的极限 $\lim\limits_{x\rightarrow\infty}=A$ 。

柯西收敛准则：

• $f$ 在 $\mathring U(x_0,\delta')$ 上有定义，且 $\lim\limits_{x\rightarrow x_0}$ 存在 $\iff\forall\varepsilon>0\quad\exists\delta(0<\delta<\delta')$ ，对任何 $x',x''\in\mathring U(x_0,\delta)$ ，有 $|f(x')-f(x'')|<\varepsilon$ 。

渐近线

函数的图像与某条直线的距离趋于0，这条直线就被称为函数的渐近线。

当 $\lim\limits_{x\rightarrow\infty}f(x)=A$ 存在时，存在水平渐近线 $y=A$ 。
若函数有无定义的点 $x_0$ ，且 $\lim\limits_{x\rightarrow x_0}f(x)=\infty$ ，则函数存在垂直渐近线 $x=x_0$ 。

斜渐近线：

设渐近线为 $y=kx+b\ (k\neq 0)$ ，则函数和渐近线的距离为

$$d=\frac{|f(x)-(kx+b)|}{\sqrt{1+k^2}}$$

当距离趋于0时， $|f(x)-(kx+b)|$ 趋于0，即

$$\lim_{x\rightarrow\infty}[f(x)-(kx+b)]=0$$

将 $x$ 提出来可以得：

$$\lim_{x\rightarrow\infty}x[\frac{f(x)}{x}-k-\frac{b}{x}]=0$$

由于 $x\rightarrow\infty$ ，可以推得

$$\lim_{x\rightarrow\infty}[\frac{f(x)}{x}-k-\frac{b}{x}]=0\\ \lim_{x\rightarrow\infty}[\frac{f(x)}{x}-\frac{b}{x}]=k$$

则可以求出 $k$ 的值：

$$k=\lim_{x\rightarrow\infty}\frac{f(x)}{x}$$

继而求出 $b$ 的值：

$$b=\lim_{x\rightarrow\infty}[f(x)-kx]$$

当 $k=0$ 时，该渐近线即为水平渐近线，因此函数不可能在同一方向上同时拥有水平渐近线和斜渐近线。

上下极限

上下极限是极限的推广形式。对于一般的数列 $\{a_n\}$，其往往不收敛于一个有穷的极限，但有一个很好的性质：假如这个数列有界，那么它一定存在一个收敛子列；假如这个数列无界，那么它一定存在一个子列趋于无穷。也就是说，我们可以通过讨论子列的极限来间接研究数列本身的性质，这就引出了上下极限的话题。

定义： 设 $\{a_n\}$ 是实数列，则 $\{a_n\}$ 一定存有极限的子列，于是给出集合 $E=\{l\in R_\infty:a_n 子列\to l,n\to l\}$，记 $\sup E=a^*,\inf E=a_*$，则它们分别为数列 $\{a_n\}$ 的上极限和下极限，记作 $\varlimsup\limits_{n\to\infty}a_n=a^*,\varliminf\limits_{n\to\infty}a_n=a_*$.

无穷小量

若 $\lim\limits_{x\rightarrow x_0}=0$ ，则称 $f$ 是 $x\rightarrow x_0$ 时的无穷小量。

推论：若 $\lim\limits_{x\rightarrow x_0}=A\iff f(x)-A$ 当 $x\rightarrow x_0$ 时是无穷小量。

1. 无穷小量必有界。
2. 两个相同类型（变化过程相同）的无穷小量，它们的和差积依旧是无穷小量。
   3.无穷小量与有界量的乘积依旧是无穷小量。

阶的比较

当 $f\rightarrow 0$ ， $g\rightarrow 0$ 时：

• $\lim\limits_{x\rightarrow x_0}\frac{f(x)}{g(x)}=0$ ，则称 $f$ 是 $g$ 的高阶无穷小，记作 $f(x)=o(g(x))\ (x\rightarrow x_0)$ ， $o$ 是非紧上界记号， $o(g)$ 表示 $g$ 所有高阶无穷小的集合。
• $\lim\limits_{x\rightarrow x_0}\frac{f(x)}{g(x)}=\infty$ ，则称 $f$ 是 $g$ 的低阶无穷小。
• $\exists K,L$ ，使得 $K<|\frac{f(x)}{g(x)}|<L$ 或 $\lim\limits_{x\rightarrow x_0}\frac{f(x)}{g(x)}=C\neq 0$ ，则称 $f$ 是 $g$ 的同阶无穷小。
• 当 $|\frac{f(x)}{g(x)}|<L$ 或 $\lim\limits_{x\rightarrow x_0}\sup\frac{f(x)}{g(x)}<\infty$ 时，记作 $f(x)=O(g(x))$ ， $O$ 是渐近上界记号，包含高阶无穷小和同阶无穷小。
• $\lim\limits_{x\rightarrow x_0}\frac{f(x)}{g(x)}=1$ ，则称 $f$ 是 $g$ 的等价无穷小，记作 $f(x)\sim g(x)\ (x\rightarrow x_0)$ 。

推论：$f=o(g)\iff f+g\sim g$

等价无穷小替换

等价无穷小替换本质上是泰勒公式的简化形式。

当 $f\sim f'\quad g\sim g'\quad x\rightarrow x_0$ 时：

1. $\lim\limits_{x\rightarrow x_0}f\cdot g=A\iff\lim\limits_{x\rightarrow x_0}f'\cdot g'=A$
2. $\lim\limits_{x\rightarrow x_0}\frac{f}{g}=A\iff\lim\limits_{x\rightarrow x_0}\frac{f'}{g'}=A$
3. 当 $f$ 和 $g$ 不等价时，$\lim\limits_{x\rightarrow x_0}(f-g)=A\iff\lim\limits_{x\rightarrow x_0}(f'-g')=A$
4. 当 $f$ 和 $-g$ 不等价时，$\lim\limits_{x\rightarrow x_0}(f+g)=A\iff\lim\limits_{x\rightarrow x_0}(f'+g')=A$

在实际使用过程中为了防止出错，通常不用加减法的替换。

常用等价无穷小替换：

当 $x\rightarrow 0$ 时：

三角函数型：

1. $\sin x\sim x$
2. $\tan x\sim x$
3. $x-\sin x\sim\frac{1}{6}x^3$
4. $1-\cos x\sim\frac{1}{2}x^2$
5. $\tan x-x\sim\frac{1}{3}x^3$
6. $\tan x-\sin x\sim\frac{1}{2}x^3$

反三角函数型：

1. $\arcsin x\sim x$
2. $\arctan x\sim x$
3. $\arcsin x-x\sim\frac{1}{6}x^3$
4. $x-\arctan x\sim\frac{1}{3}x^3$

指对幂型：

1. $e^x-1\sim x$
2. $a^x-1\sim x\ln a$
3. $\ln(1+x)\sim x$
4. $\log_a(1+x)\sim\frac{x}{\ln a}$
5. $(1+x)^\alpha-1\sim\alpha x$
6. $\sqrt[n]{1+x}-1\sim\frac{x}{n}$
7. $(1+x)^{\frac{1}{x}}\sim e$

无穷大量

若 $\lim\limits_{x\rightarrow x_0}=\infty$ 或 $+\infty$ 或 $-\infty$ ，则称 $f$ 是 $x\rightarrow x_0$ 时的无穷大量。

无穷大量必无界，无界不一定是无穷大量。

连续

函数在一点处连续：

若

$$\lim_{x\rightarrow x_0}f(x)=f(x_0)$$

则称 $f(x)$ 在 $x_0$ 处连续。

用增量来刻画函数连续： $\forall\varepsilon>0\quad\exists\delta>0$ ，当 $|x-x_0|<\delta$ 时， $|f(x)-f(x_0)|<\varepsilon$ 。

连续函数经过有限次四则运算依旧是连续函数，初等函数都是连续函数。

单侧连续：

右连续： $\lim\limits_{x\rightarrow x_0^+}f(x)=f(x_0)$
左连续： $\lim\limits_{x\rightarrow x_0^-}f(x)=f(x_0)$

函数在一点连续 $\iff$ 函数在该点左右都连续

间断点

若函数在一点处不连续，则称该点为函数的间断点。

第一类间断点：

若函数在该点左右极限都存在，则称该点为第一类间断点。

$\lim\limits_{x\rightarrow x_0^+}f(x)=\lim\limits_{x\rightarrow x_0^-}f(x)$ ：可去间断点
$\lim\limits_{x\rightarrow x_0^+}f(x)\neq\lim\limits_{x\rightarrow x_0^-}f(x)$ ：跳跃间断点

第二类间断点：

若函数在该点左右极限并非都存在，则称该点为第二类间断点。

函数在一侧不断振荡，无法取到极限：振荡间断点
函数在一侧趋于无穷，无法取到极限：无穷间断点

连续函数性质

用 $f(x)\in C[a,b]$ 表示 $f(x)$ 在闭区间 $[a,b]$ 上连续。

有界性定理：

• 若函数 $f(x)\in C[a,b]$ ，则 $f(x)$ 在 $[a,b]$ 上有界。

证：反证法，假设 $f(x)$ 在 $[a,b]$ 上无上界，则 $\exists x_n\in[a,b]$ ，使得

$$f(x_n)>n,n=1,2,\cdots$$

由此得 $\lim\limits_{n\rightarrow\infty}f(x_n)=+\infty$ ，又因为 $\{x_n\}\subset[a,b]$ 是有界数列，所以由致密性定理， $\{x_n\}$ 有收敛的子列 $\{x_{n_k}\}$ ，设 $\lim\limits_{k\rightarrow\infty}x_{n_k}=x_0$ 。

由于

$$a\leq x_{n_k}\leq b\\ a\leq x_0\leq b$$

所以 $f(x)$ 在 $x_0$ 处连续，由海涅定理得：

$$+\infty=\lim_{n\rightarrow\infty}f(x_n)=\lim_{k\rightarrow\infty}f(x_{n_k})=\lim_{x\rightarrow x_0}f(x)=f(x_0)$$

所以得到 $f(x)$ 在 $x_0$ 处不连续，与题设矛盾。

最值定理：

若函数 $f(x)\in C[a,b]$ ，则 $f(x)$ 在 $[a,b]$ 上有最大值和最小值。

证：由有界性定理得，存在上确界

$$\sup_{x\in[a,b]}f(x)=M$$

存在 $\xi\in[a,b]$ ，使 $f(\xi)=M$ ，倘若不然，对一切 $x\in[a,b]$ ，都有 $f(x)<M$ ，令

$$g(x)=\frac{1}{M-f(x)}$$

$g(x)$ 在 $[a,b]$ 上连续，且始终大于0，所以在 $[a,b]$ 上有上界，记作 $G$ ，则

$$0<g(x)=\frac{1}{M-f(x)}\leq G\\ f(x)\leq M-\frac{1}{G}$$

这与 $M$ 是 $f(x)$ 得上确界相矛盾，所以必有 $\xi\in[a,b]$ ，使 $f(\xi)=M$ ，即 $f(x)$ 在 $[a,b]$ 上有最大值。

同理可证得 $f(x)$ 在 $[a,b]$ 上有最小值。

介值定理：

• 若函数 $f(x)\in C[a,b]$ ，且 $f(a)\neq f(b)$ ，若 $\mu$ 是介于 $f(a)$ 和 $f(b)$ 之间的任何实数，则至少存在 $x_0\in(a,b)$ ，使得 $f(x_0)=\mu$ 。

不妨设 $f(a)<\mu<f(b)$ ，令 $g(x)=f(x)-\mu$ ，则 $g\in C[a,b]$ ，且 $g(a)<0$ ， $g(b)>0$ ，于是上述定理转化为根的存在定理。

• 根的存在定理：若函数 $f\in C[a,b]$ ，且 $f(a),f(b)$ 异号，则至少存在一点 $x_0\in(a,b)$ ，使得 $f(x_0)=0$

证：设集合

$$E=\{x|f(x)<0,x\in[a,b]\}$$

显然 $E$ 为非空有界数集，故由确界原理得其存在上确界 $x_0=\sup E$ 。

又因为 $f(a)<0,f(b)>0$ ，由连续函数的保号性，存在 $\delta>0$ ，使得

$$f(x)<0,x\in[a,a+\delta)\\ f(x)>0,x\in(b-\delta,b]$$

由此可见 $x_0\in(a,b)$ 。

反证法，假设 $g(x_0)\neq 0$ ，不妨设 $f(x_0)<0$ ，再由局部保号性得，存在 $U(x_0,\eta)\subset(a,b)$ ，使在其上 $g(x)<0$ ，则可以取

$$f(x_0+\frac{\eta}{2})<0\Rightarrow x_0+\frac{\eta}{2}\in E$$

这与 $x_0=\sup E$ 矛盾，故必有 $f(x_0)=0$ 。

一致连续

$f$ 定义在 $I$ 上， $\forall\varepsilon>0\quad\exists\delta>0$ ，若 $\forall x',x''\in I,|x'-x''|<\delta$ 时， $|f(x')-f(x'')|<\varepsilon$ ，则称 $f$ 在 $I$ 上一致连续。

一致连续和非一致连续的区别是：一致连续时取 $\delta$ 值与 $x$ 值无关，而非一致连续时取 $\delta$ 值会受到 $x$ 的约束。

推论： 一致连续 $\iff\{x_n'\},\{x_n''\}\subset I$ ，必有 $\lim\limits_{n\rightarrow\infty}(x_n'-x_n'')=0$ 。

证明：

必要性：

$\forall\varepsilon>0\quad\exists\delta>0$ ， $\forall x',x''\in I$ ，当 $|x'-x''|<\delta$ 时，使得 $|f(x')-f(x'')|<\varepsilon$
$\exists N>0\quad n>N$ ，使得 $|x_n'-x_n''|<\delta$
所以 $\lim\limits_{n\rightarrow\infty}(x_n'-x_n'')=0$

充分性：

反证法，假设 $\lim\limits_{n\rightarrow\infty}(x_n'-x_n'')=0$ ，$f$ 不一致连续。

$\exists\varepsilon_0>0\quad\forall\delta>0$ ，当 $|x'-x''|<\delta$ 时，使得 $|f(x')-f(x'')|\geq\varepsilon_0$
令 $\delta_n=\frac{1}{n}$ ，则 $|x_n'-x_n''|<\frac{1}{n}$ ，使得 $|f(x')-f(x'')|\geq\varepsilon_0$

所以当 $\lim\limits_{n\rightarrow\infty}(x_n'-x_n'')=0$ 时， $\lim\limits_{n\rightarrow\infty}(f(x_n')-f(x_n''))\geq\varepsilon_0\neq 0$ ，与题设矛盾，所以 $f$ 必然一致连续。

定理： 若 $f\in C[a,b]$ ，则 $f$ 在闭区间内一致连续。

证：反证法，假设 $f(x)$ 在 $[a,b]$ 不一致连续，可以在 $[a,b]$ 上取到两个数列 $\{a_n\},\{b_n\}$ ，有

$$\lim_{n\rightarrow\infty}(a_n-b_n)=0$$

此时对于 $\forall i\in N$ ，有

$$|f(a_i)-f(b_i)|\geq t$$

根据致密性定理可以得， $\{a_n\},\{b_n\}$ 分别有收敛子列 $\{a_{n_k}\},\{b_{n_k}\}$ ，并收敛于同一极限 $x_0\in[a,b]$ ，因此：

$$\lim_{n\rightarrow\infty}|f(a_{n_k})-f(b_{n_k})|=0$$

产生矛盾，所以必定 $f\in C[a,b]$ 。

复合函数的连续性

若函数 $f$ 在 $x_0$ 处连续， $g$ 在 $u_0$ 处连续， $u_0=f(x_0)$ ，则复合函数 $f\circ g$ 在 $x_0$ 处连续。

证：由于 $g$ 在 $u_0$ 处连续，$\forall\varepsilon>0$ ， $\exists\delta'>0$ ，使得当 $|u-u_0|<\delta_1$ 时，有

$$|g(u)-g(u_0)|<\varepsilon$$

又因为 $u=f(x)$ 在 $x_0$ 处连续，故 $\exists\delta>0$ ，使得当 $|x-x_0|<\delta$ 时，有 $|u-u_0|=|f(x)-f(x_0)|<\delta'$ ，又由上式可得：

$$|g(f(x))-g(f(x_0))|<\varepsilon$$

可证得 $f\circ g$ 在 $x_0$ 处连续。

用极限得方式可将上式表为：

$$\lim_{x\rightarrow x_0}g(f(x))=g(\lim_{x\rightarrow x_0}f(x))=g(f(x_0))$$

反函数的连续性

若函数 $f$ 在 $[a,b]$ 上严格单调并连续，则其反函数 $f^{-1}$ 在其定义域 $[f(a),f(b)]$ 或 $[f(b),f(a)]$ 上连续。

证：不妨设 $f$ 在 $[a,b]$ 上严格增，此时 $f^{-1}\subset[f(a),f(b)]$ ，任取 $y_0\subset(f(a),f(b))$ ，设 $x_0=f^{-1}(y_0)\in(a,b)$ 。

$\forall\varepsilon>0$ ， $\exists x_1<x_0<x_2\quad x_1,x_2\in(a,b)$ ，使得 $x_1,x_2$ 和 $x_0$ 的距离小于 $\varepsilon$ 。

设与 $x_1,x_2$ 对应的函数值为 $y_1,y_2$ ， $y_1<y_0<y_2$ ，令

$$\delta=\min\{y_2-y_0,y_0-y_1\}$$

则当 $y\in U(y_0,\delta)$ 时，有

$$|f^{-1}(y)-f^{-1}(y_0)|=|x-x_0|<\varepsilon$$

即 $f^{-1}$ 在 $y_0$ 处连续，同理可证得 $f^{-1}$ 在 $f(a)$ 处右连续，在 $f(b)$ 处左连续，所以 $f^{-1}$ 在 $[f(a),f(b)]$ 上连续。