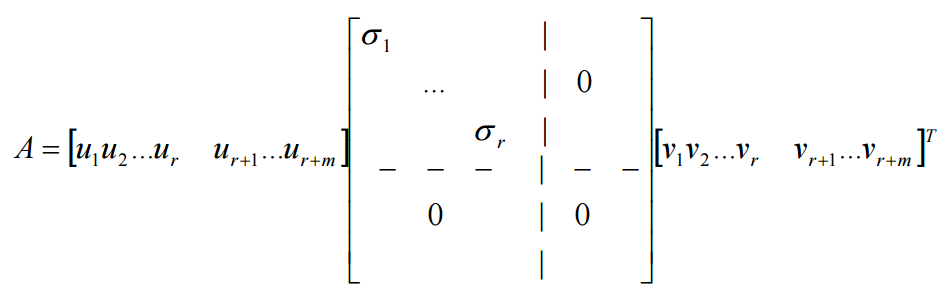矩阵基本概念
矩阵(Matrix)是线性代数中主要的研究对象,在此,我会给出在本博客中使用的所有矩阵基本符号及定义,后面所有关于线性代数的讨论都将以此作为基础。
用 m×n 个数排成 m 行的数表
a11a21⋮am1a12a22⋮am2⋯⋯⋯a1na2n⋮amn
称作 m×n 矩阵,记作 A=(aij)m×n ,其中 aij 是矩阵第 i 行第 j 列的元素,称作 (i,j) 元,元素为实数的矩阵称作实矩阵,元素为复数的矩阵称作复矩阵,两个矩阵行数列数相同则称为同型矩阵,同型矩阵对应元素相同则称作相等矩阵。
m×n 个元素全为零的矩阵称作零矩阵,记作 O 。
主对角线元素全为1的矩阵称作单位矩阵,记作 I 或 E :
I=10⋮001⋮0⋯⋯⋯00⋮1
当 m=1 时,称 Am×n 为行矩阵或行向量;
当 n=1 时,称 Am×n 为列矩阵或列向量;
当 m=n 时,称 A 为 n 阶方阵,简记为 An 。
矩阵基本运算
矩阵加法(仅限于同型矩阵):
A+B=(aij+bij)
负矩阵: A+(−A)=O
矩阵加法满足交换律和结合律。
数乘矩阵:
- λ(μA)=(λμ)A
- (μ+λ)A=μA+λA
- λ(A+B)=λA+λB
- (−1)A=−A
矩阵乘法:
C=AB
只有当左乘矩阵 A 的列数等于右乘矩阵 B 的行数时,矩阵才能相乘,所得矩阵 C 的行数与 A 的行数一致,列数与 B 的列数一致。
对乘加法则: C 的任一元素就等于这个元素所在行对应于 A 的行向量和这个元素所在列对应于 B 的列向量的点乘:
cij=k=1∑naikbkj(i=1,2,⋯,m;j=1,2,⋯,p)
矩阵乘法满足结合律和分配律,但不满足交换律。
任何矩阵和单位矩阵相乘都等于其本身。
矩阵的幂:
- AkAl=Ak+l
- (Ak)l=Akl
(AB)k=AkBk 不一定成立。
矩阵转置:
矩阵转置就是将矩阵每一元素的行列位置互换:
(aij)T=(aji)
- (AT)T=A
- (A+B)T=AT+BT
- (λA)T=λAT
- (AB)T=BTAT
矩阵的分块运算
A=A11A21⋮As1A12A22⋮As2⋯⋯⋯A1tA2t⋮Ast
分块加法运算(仅限于分块方法相同的矩阵):
A+B=A11+B11A21+B21⋮As1+Bs1A12+B12A22+B22⋮As2+Bs2⋯⋯⋯A1t+B1tA2t+B2t⋮Ast+Bst
分块数乘运算:
λA=λA11λA21⋮λAs1λA12λA22⋮λAs2⋯⋯⋯λA1tλA2t⋮λAst
分块乘法运算(对 A 列的分法和对 B 行的分法一致):
AB=C11C21⋮Cs1C12C22⋮Cs2⋯⋯⋯C1rC2r⋮Csr
Cij=k=1∑tAikBkj(i=1,2,⋯,s;j=1,2,⋯,r)
分块矩阵转置:
AT=A11TA12T⋮A1tTA21TA22T⋮A2tT⋯⋯⋯As1TAs2T⋮AstT
特殊矩阵
以下讨论的特殊矩阵均为方阵。
对角矩阵:
Λ=λ1λ2⋱λn
简记为 Λ=diag(λ1,λ2,⋯,λn)
对角矩阵的乘积和幂比较特殊:
AB=BA=a1b1a2b2⋱anbn
Λk=λ1kλ2k⋱λnk
标量矩阵(对角矩阵的特殊情况):
A=aa⋱a
上三角形矩阵:
a110⋮0a12a22⋮0⋯⋯⋯a1na2n⋮amn
下三角形矩阵:
a11a21⋮am10a22⋮am2⋯⋯⋯00⋮amn
上三角矩阵和下三角矩阵可以通过转置互相转换。
对于 n 阶上(下)三角形矩阵 A,B ,矩阵乘积 AB (或 BA )的主对角线元素刚好就是 A,B 相应主对角线元素的乘积:
AB=a1b1?⋮??a2b2⋮???⋱???⋮anbn
对称矩阵:
对阵矩阵中关于主对角线对称的两个元素相等:
aij=aji
对称矩阵转置,矩阵不发生改变: AT=A
反称矩阵:
反称矩阵中关于主对角线对称的两个元素相反,并且主对角线上的元素均为零:
aij=−aji
反称矩阵转置,矩阵中的元素取其相反数: AT=−A
任何方阵均可以表示为一个对称矩阵和一个反称矩阵之和。
分块对角矩阵:
一个分块矩阵,其主对角线上的子块全是方阵(阶数可以不同),其余子块均为零矩阵。
分块对角矩阵的性质和对角矩阵的性质类似。
初等变换和初等矩阵
为了解释矩阵的初等变换,我们需要引入同解方程组的概念。考虑一个线性方程组,以下三种操作不会影响方程组最后的解:
- 用一个不等于零的数去乘某个方程。
- 用一个数去乘某个方程后加到另一个方程上去。
- 交换两个方程的位置。
这些操作就被称为线性方程组的初等变换(Elementary transformation),经过初等变换后得到的新方程组和原来的方程组互为同解方程组。
同样的,对于矩阵而言,我们有以下三种初等行变换:
- 倍法变换:用一个非零的数乘矩阵的某行。
- 消法变换:用一个数乘矩阵的某行后再加到另一行上去,
- 换法变换:交换矩阵的两行。
矩阵的初等行变换和初等列变换,统称为矩阵的初等变换。
如果矩阵 A 经过有限次初等变换变成矩阵 B ,则称矩阵 A,B 等价,记作 A≅B 。
矩阵之间的等价关系具有如下性质:
- 自反性: A≅A
- 对称性: 若 A≅B ,则 B≅A
- 传递性: 若 A≅B,B≅C ,则 A≅C
初等矩阵:
对单位矩阵 I 施加一次初等变换得到的矩阵称为初等矩阵。
用初等矩阵左乘 A ,相当于对 A 进行对应的初等行变换;用初等矩阵右乘 A ,相当于对 A 进行对应的初等列变换。
初等倍法矩阵:
P(i[k])=1⋱1k1⋱1
初等消法矩阵:
P(i,j[k])=1⋱1⋯⋱k⋮1⋱1
初等换法矩阵:
P(i,j)=1⋱0⋮1⋯⋯1⋮0⋱1
标准形矩阵:
任何一个矩阵 Am×n 必能经过有限次初等变换化为如下形式:
G=[IrOOO]=1⋱10⋮0⋯⋯0⋮0
其中 Ir 的行数为 r ,则 0≤r≤min{m,n} , G 称为矩阵 A 在初等变换下的标准形,简称标准形矩阵。
在将矩阵变换为标准形的时候,我们会同时用到初等行变换和初等列变换,但大多数时候我们只会使用初等行变换,将矩阵变换为行阶梯形矩阵,它的特点是:
- 矩阵的所有元素全为0的行(如果存在的话)都集中在矩阵的最下面;
- 每行左起第一个非零元素(称为首非零元)的下方元素全为0。
形如:
c110⋮00⋮0c12c22⋮00⋮0⋯⋯⋯⋯⋯c1rc2r⋮crr0⋮0c1r+1c2r+1⋮crr+10⋮0⋯⋯⋯⋯⋯c1nc2n⋮crn0⋮0
行阶梯形任能继续化简为行最简形矩阵:
1⋮00⋮0⋯⋯⋯⋯0⋮10⋮0c11⋮cr10⋮0⋯⋯⋯⋯c1n⋮crn0⋮0
显然,行最简形矩阵只要再作适当的初等列变换,就能化为标准形矩阵。
行列式(Determinant)
行列式是一种对于方阵的运算,其运算结果是一个数,设 n 阶方阵 A=(aij) ,称
a11a21⋮an1a12a22⋮an2⋯⋯⋯a1na2n⋮ann
为方阵 A 的行列式,记作 ∣A∣ 或 detA 。
下面,我们主要研究行列式的计算方式及相关性质。
对角线计算法则:
对角线法则适合于计算二阶或三阶这些低阶的行列式:
对于二阶行列式:
a11a21a12a22=a11a22−a12a21
对于三阶行列式:
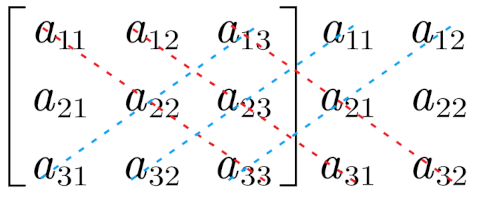
a11a21a31a12a22a32a13a23a33= a11a22a33+a12a23a31+a13a21a32− a13a22a31−a12a21a33−a11a23a32
对于高阶行列式而言,我们需要寻找更加通用的解法,这就引出了接下来的内容。
全排列与逆序数
n 个自然数 1,2,⋯,n 按照任何一种次序排成的有序数组 j1j2⋯jn 称为一个 n 级排列(Permutation),显然,不重复的 n 级排列共有 n! 个。
若规定从小到大为自然数的标准顺序,则当两个数之间不满足这个顺序时,就称作逆序,一个 n 级排列所有逆序的总和称为逆序数(Inversion number),记作 τ(j1j2⋯jn) 。
逆序数的计算方式:对于排列 j1j2⋯jn ,自 j1 开始直到 jn−1 ,逐个计算每个元素的右边比它大的元素的个数 k1,k2,⋯,kn−1 ,则该排列的逆序数为:
τ(j1j2⋯jn)=k1+k2+⋯+kn−1
我们称逆序数为奇数的排列为奇排列,逆序数为偶数的排列为偶排列,排列中任何两个数的位置对换必然会改变排列的奇偶性。
借助排列的概念,可以定义 n 行列式 ∣A∣ 的通式:
D=∣A∣=j1j2⋯jn∑(−1)τ(j1j2⋯jn)a1j1a2j2⋯anjn
或
D=∣A∣=i1i2⋯in∑(−1)τ(i1i2⋯in)ai11ai22⋯ainn
此处的 j1j2⋯jn∑ 表示对所有不同的 n 阶排列求和,一共是 n! 项。
乘积项 a1j1a2j2⋯anjn 称为行列式的一个均匀分布项,简称均布项;
(−1)τ(j1j2⋯jn) 称为该均布项的符号因子,其正负性取决于排列的奇偶性。
现在我们已经可以计算高阶行列式的值了,但排列法还是过于复杂,之后我们会了解一个更加常用且更易于理解的方法。
方阵行列式的性质
- 分行/列可加性:
a11⋮b1+c1⋮an1a12⋮b2+c2⋮an2⋯⋯⋯a1n⋮bn+cn⋮ann=a11⋮b1⋮an1a12⋮b2⋮an2⋯⋯⋯a1n⋮bn⋮ann+a11⋮c1⋮an1a12⋮c2⋮an2⋯⋯⋯a1n⋮cn⋮ann
-
转置不变:∣A∣=∣AT∣
-
若方阵 A 的第 i 行(第 j 列)乘 k 倍所得得矩阵为 B ,则 ∣B∣=k∣A∣ :
a11⋮kb1⋮an1a12⋮kb2⋮an2⋯⋯⋯a1n⋮kbn⋮ann=ka11⋮b1⋮an1a12⋮b2⋮an2⋯⋯⋯a1n⋮bn⋮ann
-
若方阵 A 经过一次换法变换化为 B ,则 ∣B∣=−∣A∣ 。
推论:若行列式任意两行/列相同,则行列式为0。
推论:若行列式任意两行/列对应元素成比例,则行列式为0。
-
消法变换不改变行列式的值,即行列式的任意行/列可以乘一个数加到另外一行/列上。
方阵行列式运算规律:
设 A,B 为 n 阶方阵, λ 为常数, m 为正整数。
- ∣λA∣=λ∣A∣
- ∣AB∣=∣A∣∣B∣
- ∣Am∣=∣A∣m
- ∣I∣=1
拉普拉斯展开(Laplace expansion)
子式: 在 n 阶方阵行列式 ∣A∣ 中,取部分行列相交形成的阶数 <n 的行列式,称作行列式 ∣A∣ 的子式。
余子式(Minor): 把元素 aij 所在的行列删除后,留下来的 n−1 阶行列式叫做元素 aij 的余子式,记作 Mij ;把 k 阶子式 N 所在的行列删除后,留下来的 n−k 阶行列式叫做子式 N 的余子式,记作 M 。
代数余子式(Cofactor):
Aij=(−1)i+jMij
叫做元素 aij 的代数余子式;
A=(−1)i1+⋯+ik+j1+⋯+jkM
叫做子式 N 的代数余子式。(其中 i 和 j 代表子式所处的行和列的序数)
定理: 对于 ∣A∣ ,其任意一行/列的所有元素与另一行/列对应元素的代数余子式乘积之和等于零,即当 i=j 时,有:
ai1Aj1+ai2Aj2+⋯+ainAjn=0a1iA1j+a2iA2j+⋯+aniAnj=0
拉普拉斯定理: 设 D 是 n 阶行列式,在 D 中取定某 k 行 (1≤k≤n−1) ,则含与此 k 行中的所有 k 阶子式与其代数余子式的乘积之和等于 D 。
运用拉普拉斯定理,可以将行列式按任意行展开:
∣A∣=ai1Ai1+ai2Ai2+⋯+ainAini=1,2,⋯,n
同理,也可以按任意列展开:
∣A∣=a1jA1j+a2jA2j+⋯+anjAnjj=1,2,⋯,n
例: 计算如下行列式
D2n=acac⋱⋰acbd⋰⋱bdbd
解:按第一行展开,可以得:
D2n=aac0⋱⋰⋯ac⋯bd⋯⋰⋱⋯bd00⋮⋮⋮⋮0d+b(−1)1+2n0⋮⋮⋮⋮0cac0⋱⋰⋯ac⋯bd⋯⋰⋱⋯bd0
D2n=adD2(n−1)+(−1)1+2n(−1)2n−1+1bcD2(n−1)=(ad−bc)D2(n−1)
以此作为递推公式,可得:
D2n=(ad−bc)D2(n−1)=(ad−bc)2D2(n−2)=(ad−bc)n−1D2=(ad−bc)n−1acbd=(ad−bc)n
范德蒙(Vandermonde)行列式:
Dn=1x1x12⋮x1n−11x2x22⋮x2n−1⋯⋯⋯⋯1xnxn2⋮xnn−1=1≤i<j≤n∏(xj−xi)
其中 ∏ 表示满足 1≤i<j≤n 的所有可能的 xj−xi 进行连乘。
归纳法证明:当 n=2 时
D2=1x11x2=x2−x1=1≤i<j≤2∏(xj−xi)
满足该结论。假设该结论对 n−1 阶范德蒙行列式成立,即
Dn−1=1x2x22⋮x2n−21x3x32⋮x3n−2⋯⋯⋯⋯1xnxn2⋮xnn−2=2≤i<j≤n∏(xj−xi)
在 Dn−1 中, i=1 的情况被去除了。
证该结论对 n 阶行列式成立,将 Dn 的第 n−1 行的 −x1 倍加到第 n 行,将第 n−2 行的 −x1 倍加到第 n−1 行,如此作下去,直到第1行的 −x1 倍加到第2行,得:
Dn=000⋮01x2−x1x2(x2−x1)⋮x2n−2(x2−x1)⋯⋯⋯⋯1xn−x1xn(xn−x1)⋮xnn−2(xn−x1)
按第一列展开得:
Dn=x2−x1x2(x2−x1)⋮x2n−2(x2−x1)⋯⋯⋯xn−x1xn(xn−x1)⋮xnn−2(xn−x1)
由行列式的性质可得:
Dn=(x2−x1)(x3−x1)⋯(xn−x1)1x2⋮x2n−21x3⋮x3n−2⋯⋯⋯1xn⋮xnn−2=(x2−x1)(x3−x1)⋯(xn−x1)2≤i<j≤n∏(xj−xi)=1≤i<j≤n∏(xj−xi)
此处用 (x2−x1)(x3−x1)⋯(xn−x1) 连乘补全了 i=1 的情况。
根据数学归纳法,可证得范德蒙行列式结论在 n≥2 时成立。
AB型行列式:
除了对角线是 b 其余全是 a 的行列式:
ba⋮aab⋮a⋯⋯⋯aa⋮b
将除第1行以外每一行都加到第1行上,得:
b+(n−1)aa⋮ab+(n−1)ab⋮a⋯⋯⋯b+(n−1)aa⋮b
由行列式性质可转化为:
[b+(n−1)a]1a⋮a1b⋮a⋯⋯⋯1a⋮b
将第1行乘 (−a) 加到下面各行上,得:
[b+(n−1)a]10⋮01b−a⋮0⋯⋯⋯10⋮b−a=[b+(n−1)a]b−a⋮0⋯⋯0⋮b−a
可得AB型行列式通式:
b+(n−1)aa⋮ab+(n−1)ab⋮a⋯⋯⋯b+(n−1)aa⋮b=[b+(n−1)a](b−a)n−1
加边法:
加边法是对拉普拉斯展开的逆用,用加边法可以求如下行列式:
x1a1⋮a1a2x2⋮a2⋯⋯⋯anan⋮xn
在行列式左侧加边,可将原式转化为:
100⋮0−a1x1a1⋮a1−a2a2x2⋮a2⋯⋯⋯⋯−ananan⋮xn
将第1行加到下面各行上,得:
111⋮1−a1x1−a10⋮0−a20x2−a2⋮0⋯⋯⋯⋯−an00⋮xn−an
这种形状的行列式被称作“爪型行列式”,求解爪型行列式:
i=1∏n(xi−ai)1x1−a11x2−a21⋮xn−an1−a110⋮0−a201⋮0⋯⋯⋯⋯−an00⋮1
各行乘 (−ai) 加到第1行:
i=1∏n(xi−ai)1+i=1∑nxi−aiaix1−a11x2−a21⋮xn−an1010⋮0001⋮0⋯⋯⋯⋯000⋮1=i=1∏n(xi−ai)(1+i=1∑nxi−aiai)
矩阵的逆
设 A 为 n 阶方阵,若存在 n 阶方阵 B ,使得
AB=BA=I
则称 A 可逆,且 B 是 A 的逆矩阵,简称 A 的逆(Inverse),记作 B=A−1 。
一般而言,我们只讨论方阵的逆。
可逆矩阵又称非奇异矩阵(Nonsingular matrix),不可逆矩阵又称奇异矩阵(Singular matrix)。
易证初等矩阵都是可逆矩阵:
- P(i[k])−1=P(i[k1])
- P(i,j[k])−1=P(i,j[−k])
- P(i,j)−1=P(i,j)
可逆矩阵基本性质:
- 可逆矩阵的逆是唯一的。
- 若 A 可逆,则 (A−1)−1=A 。
- 若 A 可逆,数 λ=0 ,则 λA 可逆,且 (λA)−1=λ1A−1 。
- 若 A 可逆,则 AT 可逆,且 (AT)−1=(A−1)T 。
- 若 n 阶方阵 A,B 皆可逆,则 AB 可逆,且 (AB)−1=B−1A−1 。
推广:若 n 阶方阵 A1,A2,⋯,As 皆可逆,则它们的乘积 A1A2⋯As 也可逆,且
(A1A2⋯As)−1=As−1⋯A2−1A1−1
- 规定 A−m=(Am)−1=(A−1)m 。
- 可逆矩阵的行列式 ∣A−1∣=∣A∣1
伴随矩阵求逆矩阵
对 n 阶方阵每一个元素求其代数余子式 Aij ,填写在原来的位置,然后再进行转置,可以写出如下方阵:
A11A12⋮A1nA21A22⋮A2n⋯⋯⋯An1An2⋮Ann
这个方阵就被称作 A 的伴随矩阵(Adjugate matrix,the adjoint of a matrix),记作 A∗ 或 adj A。
由代数余子式定理我们可以推出,矩阵与其伴随矩阵乘积的关系:
AA∗=A∗A=∣A∣I
当 A 可逆时,存在逆矩阵 A−1 使得 AA−1=I ,两边取行列式,得
∣A∣∣A−1∣=1
因此必然有 ∣A∣=0 。又因为 AA∗=∣A∣I ,可得
A−1=∣A∣1A∗
综上,我们找到了用伴随矩阵求逆矩阵的方法。
矩阵可逆定理:
-
方阵 A 可逆的充要条件是 ∣A∣=0 。
-
对于 n 阶矩阵 A,B ,只要有 AB=I ,则矩阵 A,B 皆可逆且互为逆。
-
方阵 A 可逆的充要条件是 A 可以经过有限次初等变换化为单位矩阵。
-
方阵 A 可逆的充要条件是 A 可以表示为有限个初等矩阵的乘积。
-
方阵 A 可逆的充要条件是可以只经过初等行变换化为单位矩阵。
借助矩阵的逆和初等变换的关系,可以用初等变换求逆:
[AI]elementary[IA−1]
伴随矩阵基本性质:
- ∣A∗∣=∣∣A∣A−1∣=∣A∣∣A∣n=∣A∣n−1
- (A∗)−1=(∣A∣A−1)−1=∣A∣A
- (A∗)T=(∣A∣A−1)T=∣AT∣(AT)−1=(AT)∗
- (kA)∗=∣kA∣(kA)−1=kn∣A∣k1A−1=kn−1A∗
- (A∗)∗=∣A∗∣(A∗)−1=∣∣A∣A−1∣(∣A∣A−1)−1=∣A∣n−1∣A∣A=∣A∣n−2A
- (AB)∗=∣AB∣AB−1=∣A∣∣B∣B−1A−1=∣B∣B−1∣A∣A−1=B∗A∗
广义逆矩阵
左逆和右逆:
以上我们的求逆都是对于方阵而言的,这种逆被称作两侧逆,而非方阵则不拥有两侧逆,只能分情况讨论其左逆和右逆。
对于 m×n(m=n) 的矩阵:
当 m>n 时,ATA 是一个 n×n 的方阵,则可以讨论 ATA 的逆,此时
(ATA)−1ATA=I
令 Aleft−1=(ATA)−1AT ,则
Aleft−1A=I
称 Aleft−1 为 A 的左逆。
同理,当 m<n 时,AAT 是一个 m×m 的方阵,则可以讨论 AAT 的逆,此时
AAT(AAT)−1=I
令 Aright−1=AT(AAT)−1 ,则
AAright−1=I
称 Aright−1 为 A 的右逆。
伪逆矩阵:
对于奇异矩阵,我们无法对其进行常规求逆,此时只能对其求伪逆(Pseudo-inverse),记作 A+ ,此处不讲解其具体来由和定义,只简单提一下其求法。
A 的伪逆是对超定线性方程组 Ax=b 求其最小二乘解,定义为:
A+=a→∞lim(ATA+aI)−1AT
对于实矩阵,可以用奇异值分解法(Singular Vector Decomposite,SVD) 求其伪逆:
A=UWVT
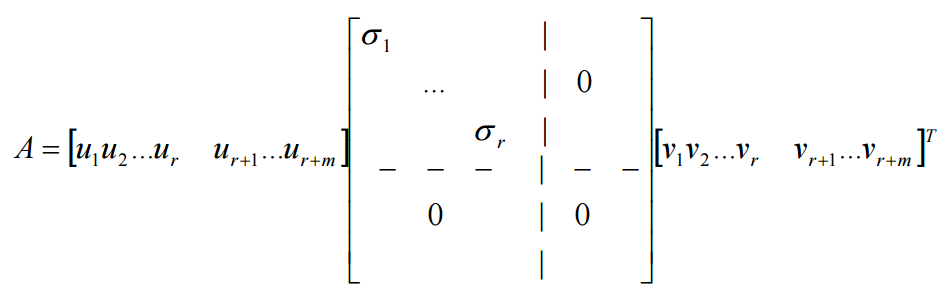
其中
AAT=U[D000]UT
ATA=V[D000]VT
用以下公式求伪逆:
A+=VD+UT
伪逆矩阵的性质:
- AA+A=A
- A+AA+=A+
- AA+=(AA+)T
- A+A=(A+A)T