机械振动
简谐振动的方程
物体在一定位置附近的位移变化满足余弦(或正弦)规律,称为简谐振动(simple harmonic motion)。
对于弹簧振子而言,在弹性限度内,弹性力可由胡克定律(Hooke’s law) 计算:
F=−kx
角频率 ω: (单位为 rad⋅s−1)
ω2=mk(或 ω=mk)
加速度 a:
a=mF=−(mk)x=dt2d2x=−ω2x
周期 T:
ωT=2πT=ω2π=2πkm
频率 ν: (单位为 Hz)
ν=T1=2πω=2π1mk
动力学特征: 简谐振动的加速度与位移 x 成正比,且方向相反。
简谐振动的微分方程:
dt2d2x+ω2x=0
简谐振动的运动方程:
x=Acos(ωt+φ)
简谐振动的速度方程:
v=dtdx=−ωAsin(ωt+φ)=ωAcos(ωt+φ+2π)
速度振幅 vm=ωA.
简谐振动的加速度方程:
a=dtdv=dt2d2x=−ω2Acos(ωt+φ)=ω2Acos(ωt+φ+π)
加速度振幅 am=ω2A.
由运动方程可知,在 t=0 时刻,有
{x0=Acosφv0=−ωAsinφ
所以
Atanφ=x02+ω2v02=−ωx0v0
相位差(phase difference): 同频率的两个简谐振动,其相位差等于它们的初相差。
Δφ=ω⋅Δt
简谐振动的能量
总能量 E,动能 Ek,势能 Ep,以弹簧振子为例:
E=Ep+EkEp=21kx2Ek=21mv2
由简谐振动方程可得
⎩⎨⎧Ep=21kA2cos2(ωt+φ)Ek=21mω2A2sin2(ωt+φ)
因为 ω2=mk,所以总能量为
E=21kA2
给定初始条件,求振幅:
21kx02+21mv02=21kA2
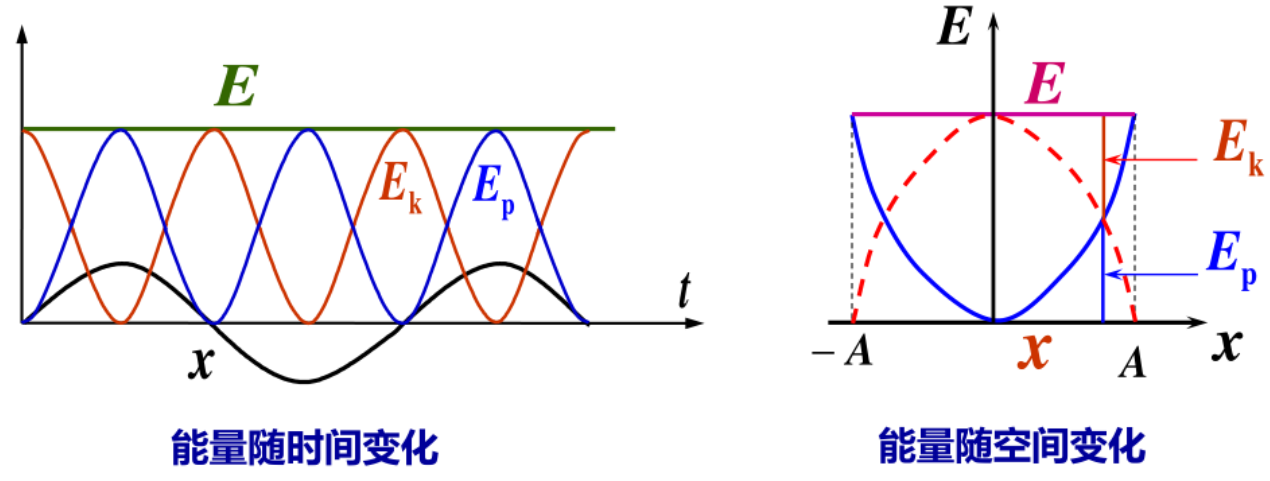
一个周期内的动能与势能平均值:
Ek=Ep=21E
Ep=T1∫0TEpdt=T1∫0T21kA2cos2(ωt+φ)dt=41kA2
Ek=T1∫0TEkdt=T1∫0T21mA2ω2sin2(ωt+φ)dt=41kA2
简谐振动的合成
旋转矢量法:
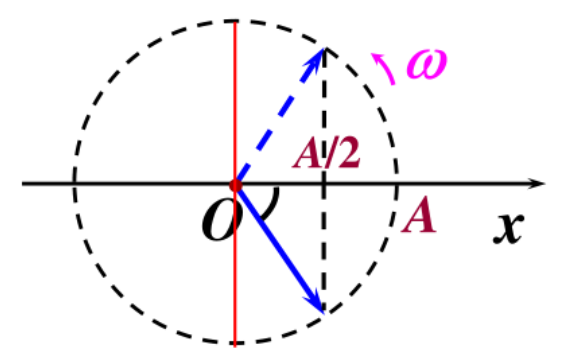
t 时刻,矢径 A 与 x 轴的夹角为 (ωt+φ),在 x 轴上的投影为 x=Acos(ωt+φ).
同频率、同方向简谐振动的合成:
对如下两个振动
{x1=A1cos(ωt+φ1)x2=A2cos(ωt+φ2)
合成后为频率为 ω 的简谐振动
x=Acos(ωt+φ)
借助旋转矢量法来计算 A 和 φ:
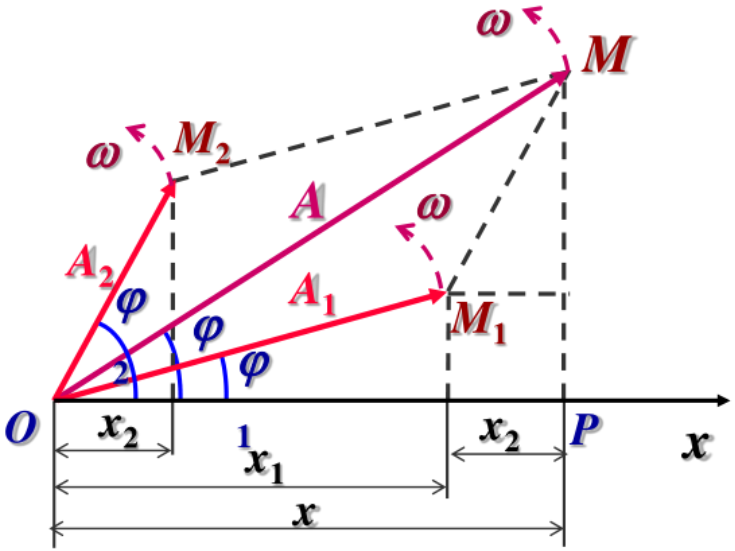
A=A12+A22+2A1A2cos(φ2−φ1)tanφ=A1cosφ1+A2cosφ2A1sinφ1+A2sinφ2
振幅的加强与减弱:
若 Δφ=φ2−φ1=2kπ,则振幅加强 A=A1+A2;
若 Δφ=φ2−φ1=(2k+1)π,则振幅减弱 A=∣A1−A2∣.
机械波
横波(transverse wave): 振动方向与波的传播方向互相垂直,一般只能在固体中传播,如绳波。
纵波(longitudinal wave): 振动方向与波的传播方向平行,纵波是靠介质疏密变化传播的,可以在固体、气体、液体三种介质中传播,如声波、弹簧波。
描述波的物理量: 波长 λ,周期 T,频率 ν,波速 u
λ=uTu=λν
- 周期(频率)由波源决定,波速由介质的性质决定。
- 不同频率的同一类波在同一介质中波速相同。
- 波在不同介质中频率不变。
平面简谐波的波函数
已知原点的振动方程为
y0=Acos(ωt+φ)
则在 x 处的一点比在原点的振动落后/提前 Δt=ux,波函数可以表示为
y=Acos[ω(t±ux)+φ]
波沿 x 轴正方向传播时取减号,沿 x 轴负方向传播时取加号。
由 ω=T2π,λ=uT,有
y=Acos[2π(Tt±λx)+φ]=Acos[2π(νt±λx)+φ]=Acos[λ2π(x±ut)+φ]
已知 P 点(坐标为 x0)的振动方程为
yP=Acos(ωt+φ)
则波函数可以表示为
y=Acos[ω(t±ux−x0)+φ]
波的相位: ω(t±ux)+φ
波线上任意两点的相位差:
Δφ=[ω(t−ux2)+φ]−[ω(t−ux1)+φ]=−λ2π(x2−x1)
波的能量与能流密度
对任意质元 dm=ρdV,有
v=∂t∂y=−Aωsinω(t−ux)
则动能和势能为
dEp=dEk=21(dm)v2=21(ρdV)A2ω2sin2ω(t−ux)
总能量为
dE=dEp+dEk=(ρdV)A2ω2sin2ω(t−ux)
能量密度(energy density of wave):
w=dVdE=ρA2ω2sin2ω(t−ux)
平均能量密度:
w=T1∫0Twdt=21ρA2ω2
波的能流: 在介质中取垂直于波面的面积 S,则单位时间内通过 S 的能量——以 S 为底、u 为高的体积内的能量,就是通过 S 的能流。
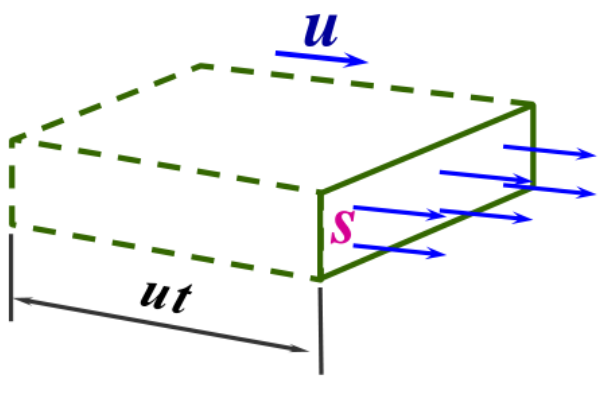
P=wuS=ρA2ω2uSsin2ω(t−ux)
平均能流:
P=wuS=21ρA2ω2uS
平均能流密度(波的强度,intensity of wave): 单位时间内通过垂直于波传播方向的单位面积上的平均能流。
I=SP=wu=21ρA2ω2u
矢量式:
I=21ρA2ω2u
波的干涉
满足相干条件的波在传播空间相遇叠加时,在叠加区域产生稳定的振动加强和减弱的分布叫波的干涉(interference of wave)。
相干条件:
- 频率相同;
- 振动方向相同;
- 相位差恒定(或相位相同)。
干涉的合振动:
两个相干波源 S1,S2 的振动方程分别为
{y10=A10cos(ωt+φ1)y20=A20cos(ωt+φ2)
它们和 P 点的距离为 r1,r2,在 P 点引起的振动分别为
⎩⎨⎧y1=A1cos(ωt+φ1−λ2πr1)y2=A2cos(ωt+φ2−λ2πr2)
合振动表示为
y=y1+y2=Acos(ωt+φ)
其中
A=A12+A22+2A1A2cos(φ2−φ1−2πλr2−r1)tanφ=A1cos(φ1−2πλr1)+A2cos(φ2−2πλr2)A1sin(φ1−2πλr1)+A2sin(φ2−2πλr2)
相遇点引起的相位差:
Δφ=φ2−φ1−2πλr2−r1
若 Δφ=2kπ,则振幅加强 A=A1+A2=Amax;
若 Δφ=(2k+1)π,则振幅减弱 A=∣A1−A2∣=Amin.
波程差:
δ=r2−r1
在两个波源同相 φ1=φ2 时,
若 δ=kλ,则振幅加强;
若 δ=(2k+1)2λ,则振幅减弱。
驻波
驻波(standing wave): 沿相反方向传播的振幅相同的两列相干波相遇叠加会形成一种波形不向前传播的波。介质中不同位置的质点在做同频率不同振幅的简谐振动。
⎩⎨⎧y1=Acos2π(Tt−λx)y2=Acos2π(Tt+λx)
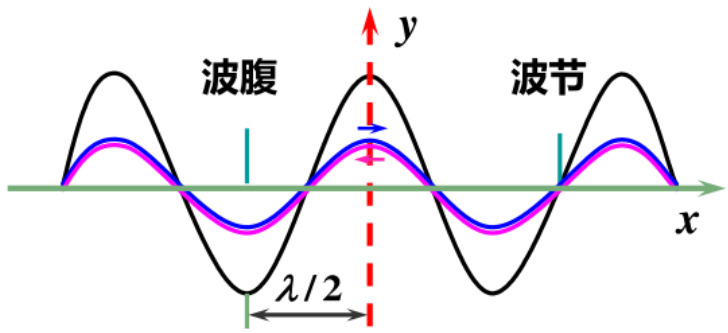
振幅:
2Acos2πλx
波腹(wave loop): 振幅最大(为 2A)的点。
x=±k2λ,k=0,1,2,⋯
波节(wave node): 始终不动的点(振幅为 0)。
x=±(2k+1)4λ,k=0,1,2,⋯
相邻波腹(波节)之间距离 Δx=2λ.
驻波方程:
y=2Acos2πλx⋅cosT2πt
相位: 驻波是分段的振动,两相邻波节间为一段,同一段振动相位相同;相邻段振动相位相反。
驻波的能量: 平均来说没有能量的传播,但各质元间仍有能量的交换,在波节和波腹之间,动能和势能不断转化。
波的反射与透射
波密介质: ρu 较大的介质。
波疏介质: ρu 较小的介质。
当波从一个介质传播到另一个介质时,一部分反射形成反射波,一部分透射形成透射波。
对反射波而言:
- 若 ρ1u1>ρ2u2,则 φ′=φ,即从波密介质传播到波疏介质,反射波与入射波同相;
- 若 ρ1u1<ρ2u2,则 φ′=φ−π,即从波疏介质传播到波密介质,反射波有相位 π 的突变,称为半波损失(half-wave loss)。
对透射波而言:无论 ρ1u1>ρ2u2 还是 ρ1u1<ρ2u2,均有 φ′=φ,即透射波总是与入射波同相。
反射形成的驻波:
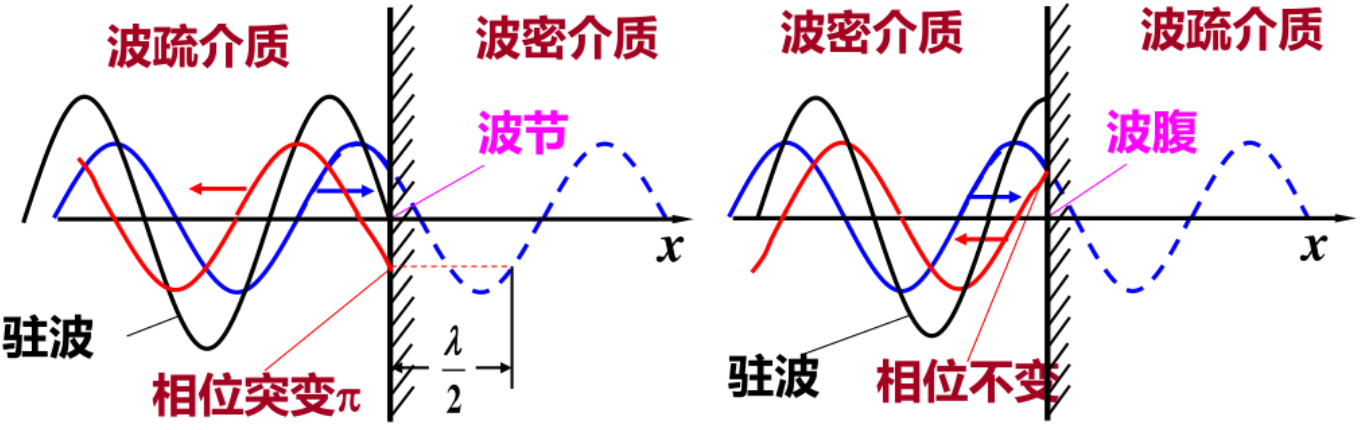
当波从波疏介质垂直入射到波密介质界面上反射时,有半波损失,形成的驻波在界面处为波节;
当波从波密介质垂直入射到波疏介质界面上反射时,无半波损失,形成的驻波在界面处为波腹。
弦线上的驻波: 对于具有一定长度且两端固定的弦线来说,形成驻波时,弦线两端为波节,所以波长和弦线长度之间满足
L=n2λ,n=1,2,3,⋯
允许存在的波长或频率为
λn=n2L,νn=λu=n2Lu
称为固有波长或固有频率,其中最低的频率被称作基频,几倍于基频的频率被称作几谐频。
静电场
电荷与库仑定律
电荷的量子化: 物体所带的电荷量只能取分立的不连续量值,称为电荷的量子化。
q=ne,n∈Z
电荷量的基本单位是电子电荷 e=1.602×10−19C.
电荷守恒定律: 一个不与外界交换电荷的系统,电量的代数和始终保持不变。
库仑定律(Coulomb’s law): 在真空中,两个静止的点电荷之间的相互作用力的大小与它们电荷电量的乘积成正比,与它们之间距离的平方成反比,作用力的方向相反。
真空中的库伦定律:
F=kr2q1q2er
静电力常量 k=9.0×109N⋅m2⋅C−2
真空介电常数 ε0=4πk1=8.85×10−12C2⋅N−1⋅m−2
电介质中的库伦定律:
F=4πε0εr1r2q1q2er=4πε1r2q1q2er
电介质的相对介电常数 εr(≥1)
电介质的介电常数 ε=ε0εr
线密度 λ=dldq,面密度 σ=dsdq,体密度 ρ=dVdq
电场强度
电场的定义(q0 为物体所带电荷量,F 为物体所受电场力):
E=q0F
电场具有可叠加性:
E=q0i=1∑nFi=i=1∑nEi
场强的计算:
将带电体分成无数个电荷元 dq,其在空间距离为 r 的某点处的场强为
dE=4πε01r3q1q2r
选取适当的坐标系,对 dE 的各个分量进行积分
Ex=∫dEx,Ey=∫dEy,Ez=∫dEzE=Exi+Eyj+Ezk
例: 真空中有一均匀带电直线,长为 l、总电量为 q,求:带电直线外一点 O′(O 点距直线一端距离为 a,OO′ 距离为 a)的场强。
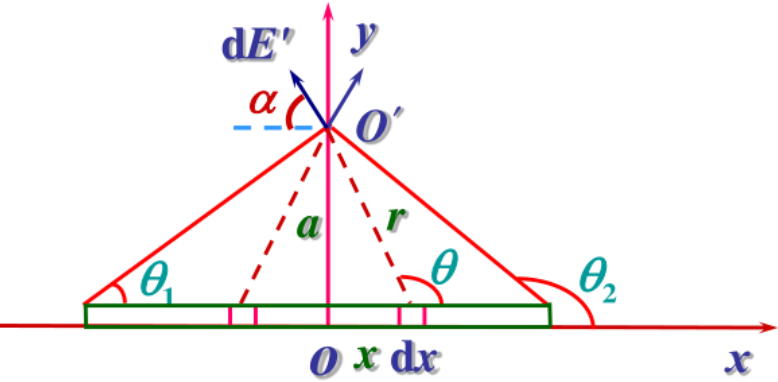
解:
dE′=4πε01r2λdx
以 O 为原点建立直角坐标系,在 x 轴和 y 轴上对场强进行分解,则
ExEy=∫qdEx=−∫qdE′cosα=∫qdEy=∫qdE′sinα
计算场强的 x 分量:
Ex=∫q4πε01r2λdxcosθ
又因为 r2=a2+x2=a2csc2θ,所以
Ex=∫θ1θ24πε0a2csc2θλacsc2θcosθdθ=∫θ1θ24πε0aλcosθdθ=4πε0aλ(sinθ2−sinθ1)
计算场强的 y 分量:
Ex=∫q4πε01r2λdxsinθ
同理可得
Ey=∫θ1θ24πε0aλsinθdθ=4πε0aλ(cosθ1−cosθ2)
合电场为
E=Exi+Eyj
当带电直线无限长时,θ1→2π,θ2→π
E=Ey=2πε0aλ
当带电直线一半无限长时,θ1→0,θ2→π
Ex=−4πε0aλ,Ey=4πε0aλ
例: 计算均匀带电圆环轴线上 P 点的场强。
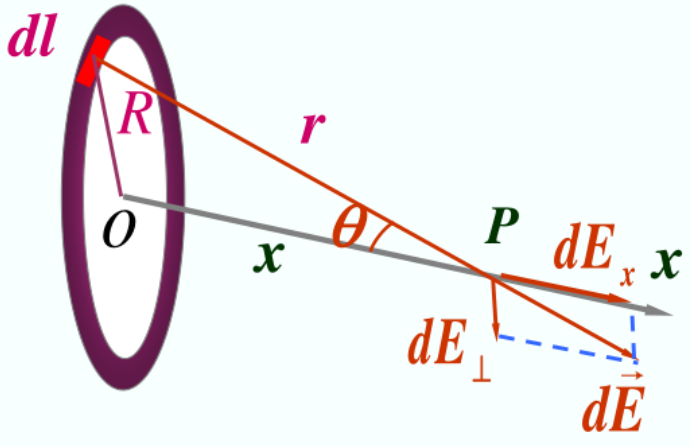
解:
dExE⊥=4πε0r2λdlcosθ=0
因为 cosθ=rx,r2=R2+x2,所以
E=∫dEx=∫02πR4πε0r2λdlcosθ=4πε01(R2+x2)23qx
在圆环中心处时,x=0,E=0.
在 x 远大于 R 时,E=4πε0x2q.
对于均匀的带电圆盘,我们可以将其看作为无数个圆环的组合,最终可以得到轴线上的场强为
E=2ε0σ(1−R2+x2x)
对于无限大的平面,R→∞,则场强为
E=2ε0σ
电通量与高斯定理
电位移矢量:
D=ε0E+P
单位体积电介质中电偶极矩的矢量和称为电极化强度矢量,以 P 表示,单位为 C⋅m2
P=ΔV∑Pmolecule
极化强度与电场强度具有以下关系:
P=σ′=εrεr−1σ=ε0(εr−1)E
定义电极化率 χe=εr−1,则
P=ε0χeE
对于各向同性介质,D 与 E 的关系为
D=ε0εrE=εE
电通量的计算:
- 平面、均匀电场:
Φe=D⋅S=DScosθ
- 曲面、任意电场:
dΦe=D⋅dS=Dd(Scosθ)Φe=∫SdΦe=∫SD⋅dS
- 闭合曲面、任意电场:
Φe=∮SdΦe=∮SD⋅dS
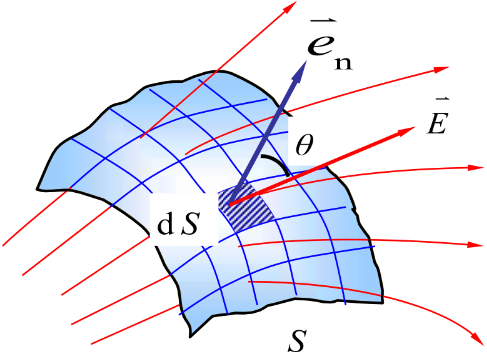
高斯定理(Gauss’s law): 电场是有源场,通过任意闭合曲面 S (称为高斯面)的电通量,等于该闭合曲面包围的自由电荷的代数和,与 S 外的电荷无关,即
∮SD⋅dS=Sin∑qi
利用高斯定理求静电场的分布: 选取的高斯面要通过待求场电,且包围部分或全部电荷;高斯面的形状由场的对称性决定,使曲面上各部分的法线 n 要么与 D 垂直,要么与 D 平行,且 n 与 D 平行的那部分曲面上各点 D 的相等。
1. 球对称的情况:
电场的方向与球表面法线的方向平行,即
dS=dnD∥dS
电荷在球上均匀分布:
D⋅4πr2D⋅4πr2=Q=∫rρ(r)4πr2dr
例: 求均匀带电球面(半径为 R,电量为 q)的电场分布。
解:当 r>R 时,
∮SD⋅dS=D⋅4πr2=q
则
DE=4πr2q=4πεr2q
当 r<R 时,
∮SD⋅dS=0
则
DE=0=0
2. 柱对称的情况:
对于无限长均匀带电圆柱面,有
∮SD⋅dS=∫侧面D⋅dS+2∫底面D⋅dS
电场方向与底面垂直,所以 ∫底面D⋅dS=0,于是
∮SD⋅dS=∫侧面D⋅dS=D⋅2πrl
电荷在圆柱面上均匀分布:
D⋅2πrlDE=λl=2πrλ=2πεrλ
3. 面对称的情况:
对于无限大均匀带电平面,将穿过平面的圆柱面当作高斯面,则有
∮SD⋅dS=∫ΔS1D⋅dS+∫ΔS2D⋅dS+∫侧面D⋅dS
电场方向与侧面垂直,所以 ∫侧面D⋅dS=0,于是
∮SD⋅dS=D⋅ΔS1+D⋅ΔS2=2D⋅ΔS=S∑qi
电荷在平面上均匀分布:
2D⋅ΔSDE=σΔS=2σ=2εσ
电势与静电场的环路定理
静电场的环路定理(Circuital theorem): 静电场是保守力场,电场力做功与路径无关,只与起点与终点的位置有关,即静电场沿任何闭合环路做功为零。
∮LE⋅dl=0
电势能(Electric potential energy): (相对量,单位为焦耳 J)
Wa−Wb=Aab=qo∫abE⋅dl
理论上通常取无穷远处的电势能为零,则 q0 在 a 点处的电势能为
Wa=∫a∞q0E⋅dl
电势(electric potential): (电场本身的性质,单位为伏特 V)
Ua=q0Wa=∫a参考点E⋅dl
电势差(电压):Uab=Ua−Ub=∫abE⋅dl
电场力做功:Aab=q0(Ua−Ub)
电势零点(参考点)的选取:
- 电荷分布是有限区域时,通常选择无穷远处为电势零点。
- 电荷分布扩展到无穷远处的带电体组成的系统,应选取有限远处为电势零点。
点电荷系电场中的电势:
UP=i=1∑nUPi=i=1∑n4πεriqi
连续带电体电场中的电势:
dUPUp=4πε0rdq=∫4πε0rdq
例: 计算半径为 R,所带电量为 q 的均匀带电圆环轴线上一点 P 的电势。

解:对电荷元 dq=λdl,有
dU=4πε0rdq
积分得
U=∫0q4πε0rdq=4πε0R2+x2q
在圆环中心处时,x=0,U=4πε0Rq.
在 x 远大于 R 时,U=4πε0xq.
等势面(equipotential surface): 电势相同点形成的曲面称为等势面。
- 在静电场中,沿等势面移动电荷,电场力做功为零。
- 静电场的电场线与等势面正交,电场线方向指向电势降落的方向。
- 相邻等势面的电势量值间隔相等,所以等势面密集处场强大,反之场强小。
静电平衡(Electrostatic balance): 放置在静电场中的导体,产生静电感应现象,当导体中没有电荷做宏观运动的状态时,称为静电平衡状态。
当带电导体处于静电平衡时,电荷分布满足:
- 导体上的电荷只能分布在导体表面上;
- 曲率越大处,电荷面密度越大,附近的电场更强。
电容器
电容器的电容(the capacitance of capacitors):(单位为法拉 F)
C=UABq
决定电容器电容的因素:电容器的大小、形状、板间电介质。
常见电容器的电容计算:(设 A 板所带电荷量为 q,B 板所带电荷量为 −q)
1. 平板电容器:
公式:
C=4πkdεrS
近似求法:
E=εσUAB=εσd=εSqdC=UABq=dεS
2. 圆柱形电容器:
E=2πεrλUAB=∫ABE⋅dl=2πελlnRARBC=UABq=lnRARB2πεl
3. 球形电容器:
E=4πεr2qUAB=∫ABE⋅dl=4πεq(RA1−RB1)C=UABq=RB−RA4πεRARB
电容器的能量:
We=21CQ2=21CU2=21UQ
静电场的能量
电场能量密度:
we=21εE2=21DE
电场的总能量:
We=∫VwedV=∫21εE2dV
其中 V 为电场空间的体积,对于球分布的场空间,有
dV=4πr2dr
对于轴分布的场空间,有
dV=2πrldr
稳恒磁场
恒定电流
电流(current): 电流强弱 I 定义为单位时间通过导体任一横截面积的电量,单位为安培 A,即
I=dtdq
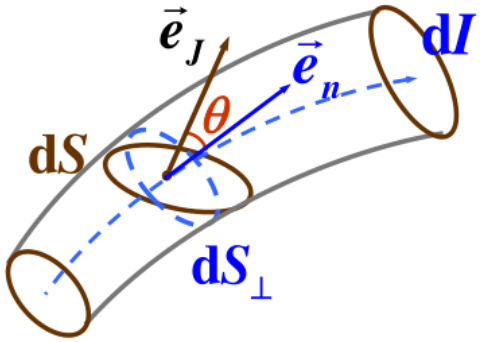
电流密度矢量: 电流密度矢量方向表示该点电流方向,其数值等于通过该点单位垂直截面的电流,即
J=dSdIen
电流 I 是矢量场 J 的通量,满足如下关系:
I=∫SJ⋅dS
欧姆定律(Ohm’s law): 通过一段导体的电流与导体两端电压成正比,即
I=RU=GU
电阻 R,单位为欧姆 Ω,计算公式为
R=∫Sρdl
其中 ρ 为电阻率。
电导 G=R1,单位为西门子 S=Ω−1.
电动势(Electromotive force): 将单位正电荷由负极板移到正极板的非静电力所做的功称为电动势,即
E=qW=∮LEK⋅dl
其中非静电场强 EK=qFK.
磁感应与毕奥-萨法尔定律
磁感应强度: (单位为特斯拉 T,方向为电荷受力为零的运动方向)
B=qvdFmax
毕奥-萨法尔定律(Biot-Savart law):
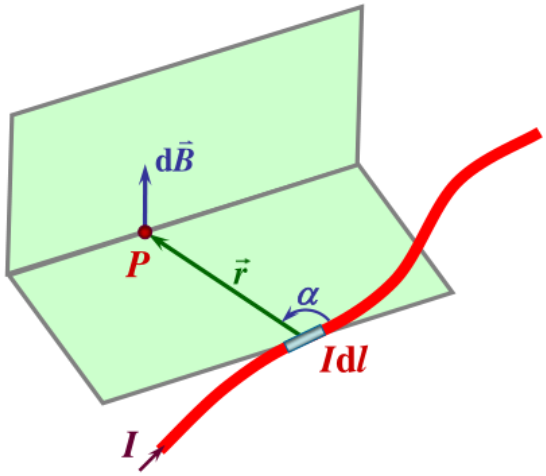
电流元 Idl 在 P 处产生的磁场磁感应强度为
dB=4πr3μ0Idl×r
真空磁导率 μ0=4π×10−7T⋅m⋅A−1.
dB 的大小为
dB=4πr2μ0Idlsinα
dl×r 方向可根据右手法则判断。
载流导线所产生的磁场磁感应强度为
B=∫LdB=∫L4πμ0r3Idl×r
1. 载流直导线的磁场:
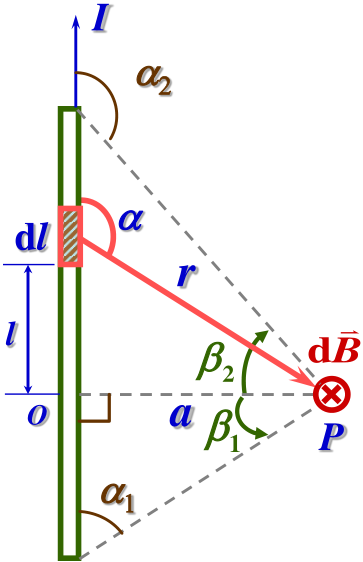
dBB=4πr2μ0Idlsinα=∫L4πr2μ0Idlsinα
由 l=acot(π−α),r=αcscα,可得
B=∫α1α24πaμ0Isinαdα=4παμ0I(cosα1−cosα2)=4παμ0I(sinβ2−sinβ1)
结论:
- 电流元或一段载流直导线在其延长线上不产生磁场。
- 无限长载流直导线产生的磁场 B=2παμ0I.
2. 载流圆形线圈轴线上的磁场:
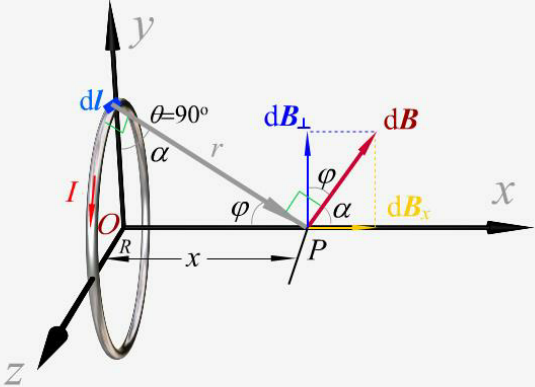
B=∫LdB⋅sinφ=∫L4πr2μ0Idl⋅sinφ
由 sinφ=R2+x2R,可得
B=2μ0⋅(R2+x2)23R2I
在圆形线圈中心处时,x=0,B=2Rμ0I.
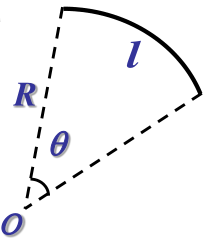
结论: 半径为 R,中心角为 θ 的载流圆弧,在圆心处产生的磁场
B=2Rμ0I2πθ=2Rμ0I2πRl
磁通量与高斯定理
磁通量的计算: 通过给定曲面的磁感线的数量,用 Φm 表示,单位为韦伯 Wb。
dΦm=B⋅dS=BdS⊥=BcosθdSΦm=∫SdΦm=∫SB⋅dS
磁场高斯定理: 磁场是无源场,对于任意曲面 S,进入曲面的磁感线和穿出曲面的磁感线数量相等,即
∮SB⋅dS=0
例:在通有电流 I 的无限长直导线旁有一矩形回路,且两者共面,求通过该回路所包围面积的磁通量。
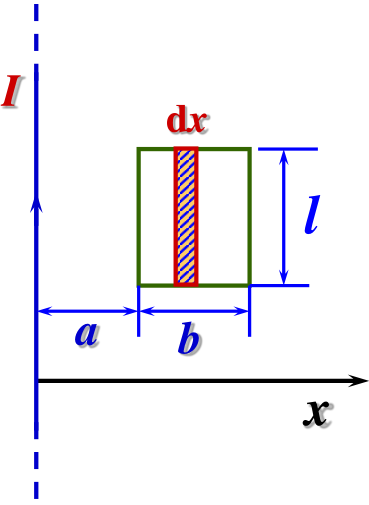
解:取直电流处为坐标原点,向右为 x 轴,则在 S 面内任一点的磁感应强度为
B=2πxμ0I
通过面积元的磁通量为
Φm=∫SB⋅dS=∫SB⋅dS=∫aa+b2πxμ0Ildx=2πμ0Illnaa+b
安培环路定理
在磁介质存在时,介质中磁感应强度由外加磁场和介质磁化共同作用,即
B=B0+μ0M
引入磁场强度:(单位为 A⋅m−1)
H=μB0−M
单位体积分子磁矩的矢量和称为磁化强度,以 M 表示,单位为 A⋅m−1
M=ΔV∑Pm
定义介质的磁化率 χm=μr−1,对于各向同性非铁磁介质,磁化强度与磁场强度成比例关系:
M=χmH
综上所述,对于各向同性非铁磁介质,H 与 B 的关系为
H=μ0μrB=μB
安培环路定理(Ampere circuital theorem): 环路内外所有传导电流产生的磁场强度的线积分,等于环路内传导电流的代数和。
∮LH⋅dl=∑Ii
真空中的安培环路定理:
∮LB⋅dl=μ0∑Ii
1. 长直螺线管内的磁场:
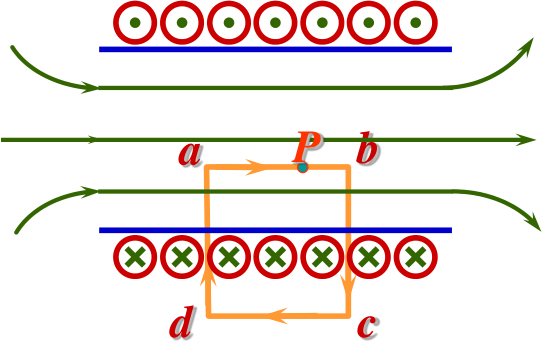
∮LH⋅dl=∫abH⋅dl=abH=∑Ii=ablNIH=nIB=μnI
单位长度匝数 n=lN.
2. 环形螺线管内的磁场:
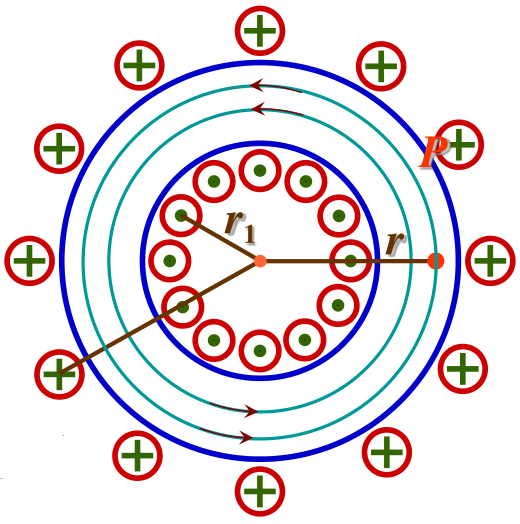
∮LH⋅dl=H⋅2πr=∑Ii=NIH=2πrNIB=2πrμNI≈lμNI=μnI
3. 无限长载流圆柱导体内外的磁场:
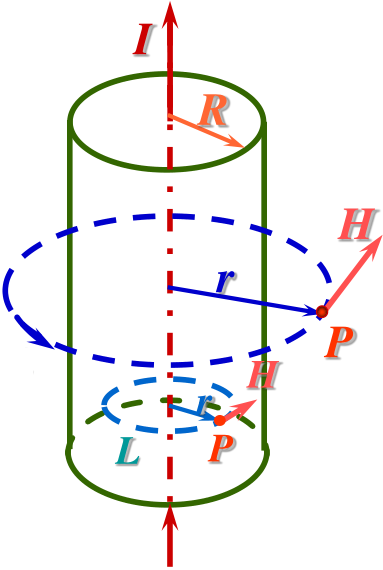
∮LH⋅dl=H⋅2πr
r>R 时,
∑Ii=IH=2πrIB=2πrμ0I
r<R 时,
∑Ii=πR2Iπr2=R2Ir2H=2πR2IrB=2πR2μIr
例:求通过无限长载流圆柱面的矩形回路的磁通量。
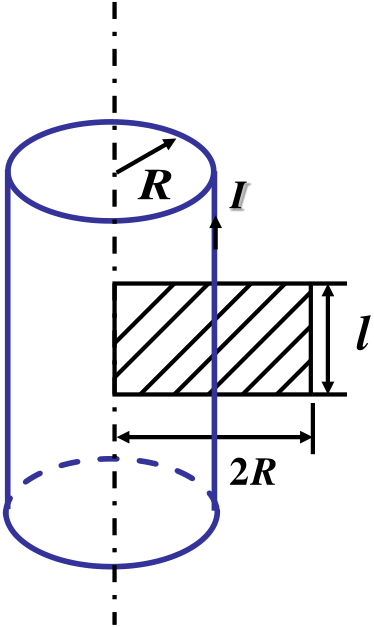
解:无限长载流圆柱面内外的磁场为
r>R,B=2πrμ0Ir<R,B=0
则磁通量为
Φm=∫SB⋅dS=∫SB⋅dS=∫R2R2πrμ0Ildr=2πμ0Illn2
磁场中的作用力
安培力: 磁场对载流导线的作用力,方向按右手法则。
dFF=Idl×B=∫LIdl×B
对于均匀磁场,直导线的安培力大小为
F=BIlsinθ
磁场对载流线圈的作用力:
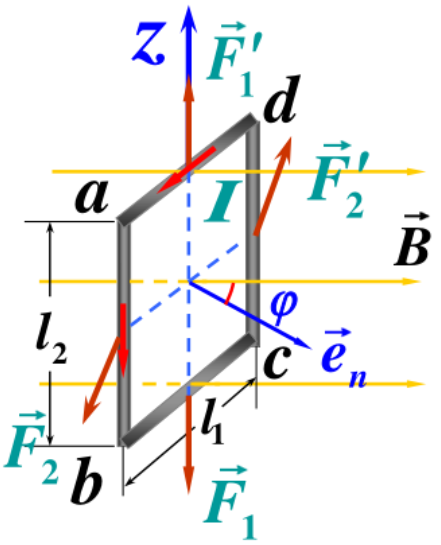
磁矩: 描述线圈本身特性的物理量。(N 为线圈匝数)
Pm=NIS⋅n
线圈在磁场中所受磁力矩为
MM=Pm×B=PmBsinθ
磁力矩所做的功为
W=∫Φm1Φm2IdΦm
洛伦兹力(Lorentz force): 磁场对运动电荷的作用力。
FmFm=qv×B=qvBsinθ
对于正电荷,F 和 v×B 同方向;对于负电荷,F 和 v×B 反方向。
带电粒子在磁场中的运动:
-
当 v∥B 时,粒子作匀速直线运动,且 F=0.
-
当 v⊥B 时,粒子作匀速圆周运动,且
F=qv0B=mRv02
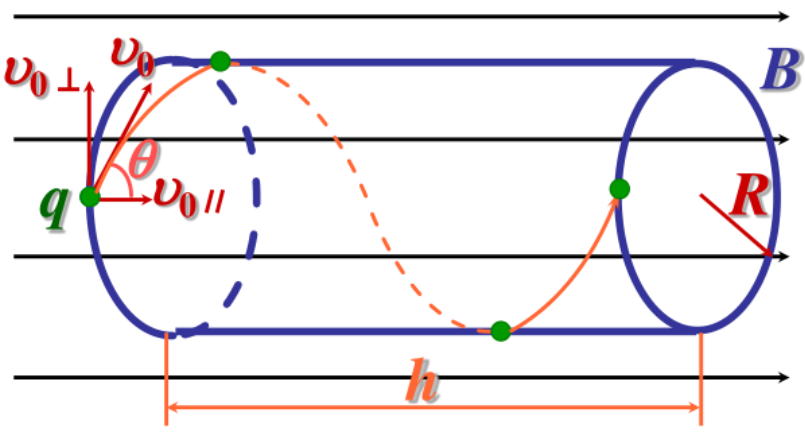
- 当 v 和 B 所成夹角为 θ 时,粒子作螺旋运动,且
h=v∥T=qB2πmvcosθ
磁场的能量
自感能量: L 为自感系数
Wm=21LI2
磁场能量密度:
wm=2μB2=21BH=21μH2
磁场的总能量:
Wm=∫VwmdV=∫21μH2dV=∫2μB2dV
电磁场理论
电磁感应
法拉第电磁感应定理: 通过回路所包围面积的磁通量发生变化时,回路中产生的感应电动势与磁通量对时间变化率的负值成正比,即
Ei=−dtdΦI=−R1dtdΦ
通过回路中任一截面感应电量为
q=∫t1t2Idt=R1∫Φ1Φ2dΦ=R1(Φ1−Φ2)
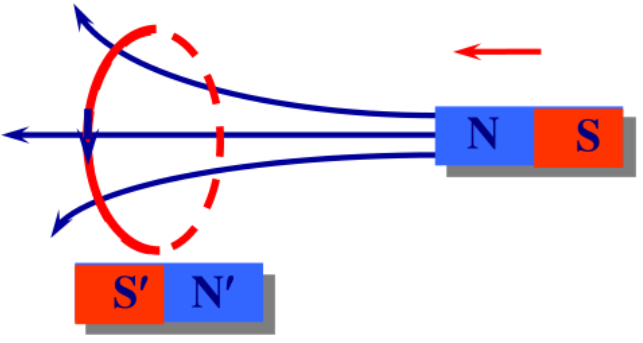
楞次定律(Lenz’s law): 闭合回路中产生的感应电流,总是使它自己产生磁场反抗任何引起感应电流的变化。
动生与感生电动势
动生电动势的计算:
电磁感应法: 适用于闭合回路整体在磁场中转动或平动的情形。
对于某时刻,磁通量 Φ 满足与时间 t 的关系式
Φ(t)=∫SB⋅dS
则电动势
Ei=dtdΦ=dtd∫SB⋅dS
利用楞次定律来判断感应电流的方向。
定义法: 适用于求解一段不闭合导体。
Ei=∫l(v×B)⋅dl
感应电流方向为 v×B 顺着 l 的方向。
例:导线 L 在均匀磁场中绕 O 以 ω 做匀速转动,求感应电动势的大小和方向。
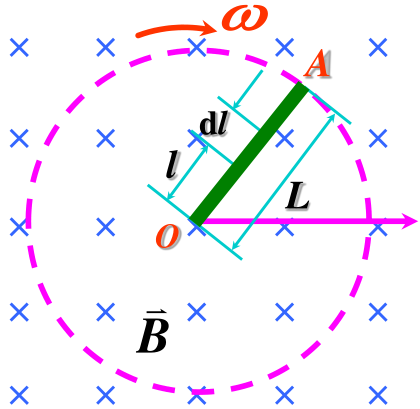
解:
dEi=(v×B)⋅dl=Bvdl
方向由 O 指向 A.
Ei=∫LBvdl=∫0LBωldl=21BωL2
感生电动势: 涡流电场提供了对电荷作用的非静电力,由此产生了感生电动势。
Ei=∮LEk⋅dl=−dtdΦm
又因为 Φm=∫SB⋅dS,所以
∮LEk⋅dl=−∫S∂t∂B⋅S
例:如图所示,在一无限长直电流的右侧有一共面的矩形回路,设 I=I0sinωt,且 a,b,l,I0,ω 均为常量,求回路中产生的感应电动势。
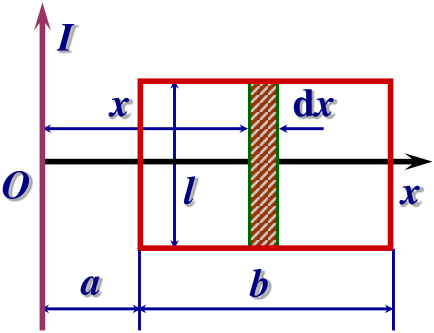
解:回路中的磁通量为
dΦmΦm=B⋅dS=2πxμ0Ildx=∫S2πxμ0Ildx=2πμ0I0lsinωtlnaa+b
感生电动势为
Ei=−dtdΦm=−2πμ0I0lωcosωtlnaa+b
位移电流
充、放电时,极板间没有传导电流,但有变化的电场,且 dE 方向与外电路的电流同向。为了解决电流不连续的问题,我们人为引入位移电流(displacement current) Id 的概念,使得全电流 I全=I+Id.
Jd=∂t∂DId=dtdΦe=∫∂t∂D⋅dS
位移电流和传导电流在产生磁场方面是等效的,但产生原因不同,且传到电流会产生焦耳热,位移电流不产生焦耳热。
全电流定律: 假设位移电流的磁效应与传导电流相同,则有
∮LH⋅dl=∫S(J+∂t∂D)⋅dS=I全
该定律适用于非稳恒磁场的情况。
麦克斯韦方程组
积分形式:
- ∮SD⋅dS=q
- ∮SE⋅dl=−∫∂t∂B⋅dS
- ∮SB⋅dS=0
- ∮LH⋅dl=∫S(J+∂t∂D)⋅dS
微分形式:
- ∇×H=J+∂t∂D
- ∇×E=−∂t∂B
- ∇×B=0
- ∇×D=ρ
电磁媒质的本构关系式:
D=εEB=μHJ=σE
ε 为介电常数,μ 为磁导率,σ 为电导率。
电磁波
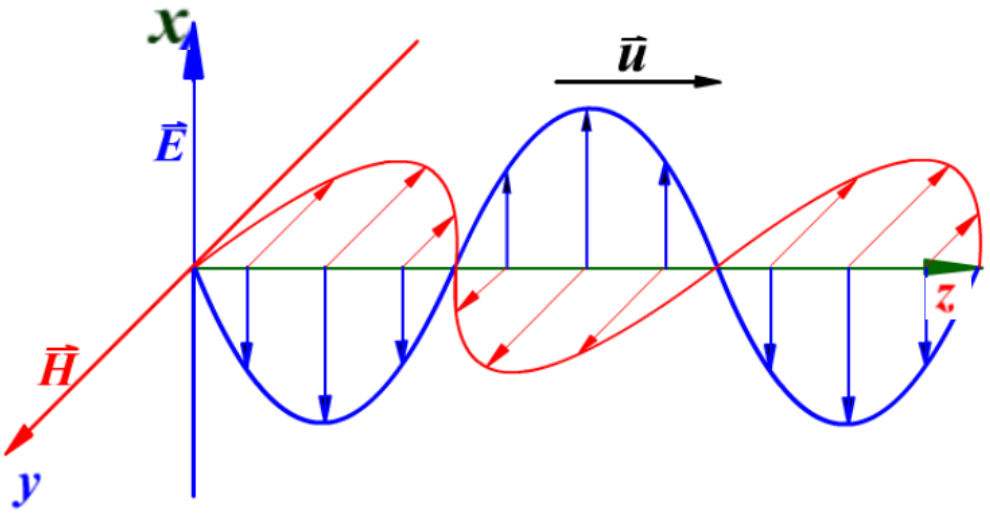
平面电磁波的波动方程:
Ex=E0cosω(t−uz)Hy=H0cosω(t−uz)
电磁波在介质中的传播速度 u=με1=μrεrc,在真空中的传播速度和光速 c 一致。
E 与 H 的大小关系满足
∂z∂H(z,t)=−ε∂t∂E(z,t)
在介质中 εE=μH;
在真空中 E=cB.
电磁波的能量: 以电磁波形式传播出去的电磁能量称为辐射能(radiation energy)。
能量密度:
w=we+wm=21εE2+21μH2
能流密度:
S=wu=21u(εE2+μH2)
用坡印廷矢量(Poynting vector) 表示为
S=E×H
将电磁波的能流密度对时间取平均值,得到电磁波的强度:
I=S=μεE2=εμH2
对平面电磁波有
I=T1∫0TE0H0cos2ω(t−uz)dt=21E0H0
光的干涉
光的相干性
相干条件:
- 频率相同;
- 振动方向相同;
- 相位差恒定;
- 振幅不能相差太大;
- 光程差不能相差太大。
相干强度:
I=I1+I2+2I1I2cosΔφ
光程差(optical path difference): 在折射率为 n 的介质中传播的几何路径为 r,光程 L=nr,相位变化为
Δφ=2πλnr=2πλL
初相相同的光束相遇时的光程差和相位差:
δ=n2r2−n1r1Δφ=λ2πδ=λ2π(n2r2−n1r1)
当 n=n1=n2 时,δ=n(r2−r1).
利用光程差判断干涉加强或减弱:
Δφ=λ2πδ={2kπ(2k+1)π⇒δ=⎩⎨⎧kλ(2k+1)2λ明纹暗纹
获得相干光的方法:
- 分波阵面法:杨氏双缝、菲涅耳双镜、劳埃德境(验证半波损失);
- 分振幅法:薄膜干涉、劈尖干涉、牛顿环。
分波阵面干涉
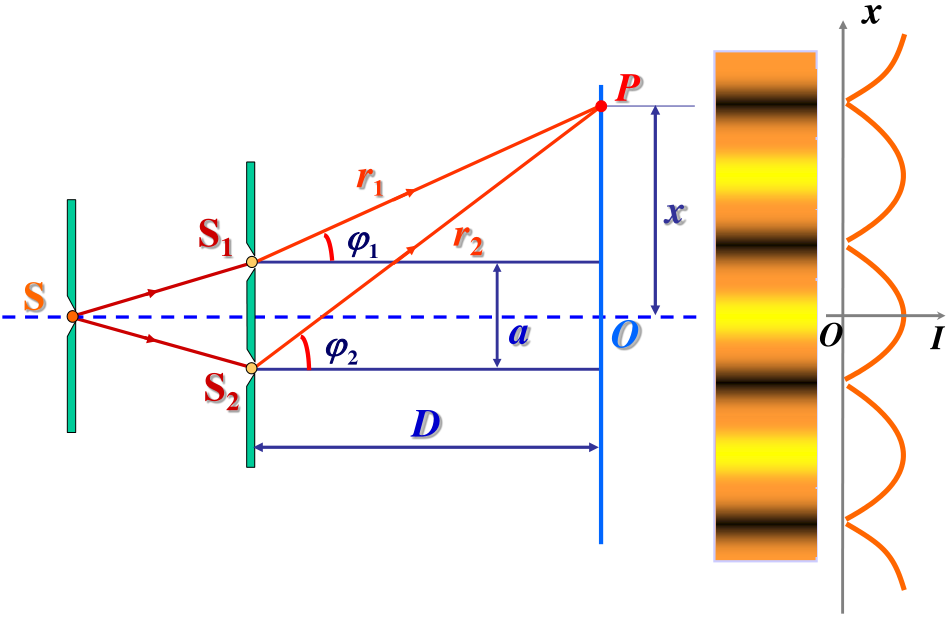
⎩⎨⎧r12=D2+(x−2a)2r12=D2+(x+2a)2r22−r12=2ax
光程差:
δ=r2−r1=r1+r22ax≈2D2ax=Dax
条纹宽度:
Δx=aDλ
条纹位置:
x=⎩⎨⎧kaDλ(2k+1)aD⋅2λ明纹暗纹
双缝后加薄膜: 相邻明纹间距不变。
δ=(n2−n1)d=kλ
分振幅干涉
薄膜干涉(film interference):等倾干涉
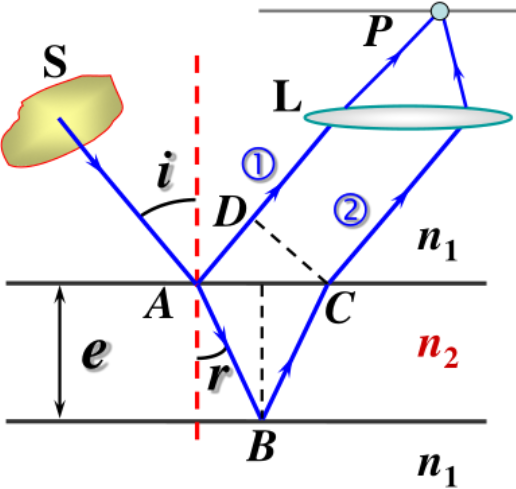
总光程差:
δ=2en22−n12sin2i+(2λ)
其中 2λ 为半波损失,反射光有半波损失,透射光没有半波损失。
垂直入射时(i=0):
δ=2n2e+(2λ)=⎩⎨⎧kλ(2k+1)2λ明纹暗纹
反射光的干涉和透射光的干涉是互补的。
增透膜与增反膜:
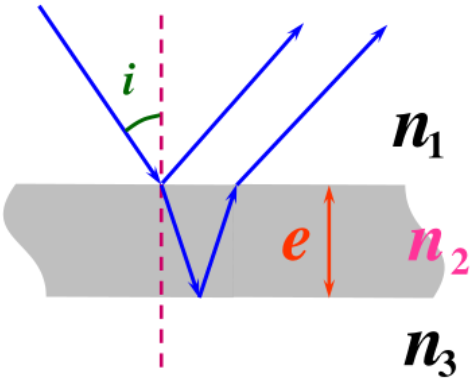
当 {n1<n2>n3n1>n2<n3 时,反射光考虑半波损失;
当 {n1<n2<n3n1>n2>n3 时,反射光不考虑半波损失。
增透膜使用反射光减弱条件或透射光加强条件。
例:n1<n2<n3 时,增透膜宽度满足
2n2e=(2k+1)λ⇒e=4n2λ(2k−1)
增反膜使用反射光加强条件或透射光减弱条件。
例:n1<n2>n3 时,增反膜宽度满足
2n2e+2λ=kλ⇒e=4n2λ(2k−1)
劈尖干涉(wedge interference):等厚干涉
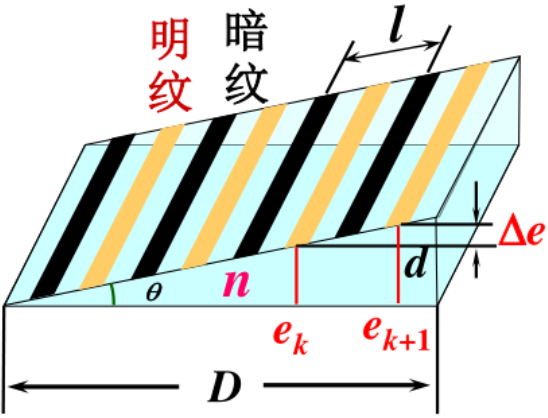
相邻两条纹(明纹或暗纹)间隔对应的的薄膜厚度差为
Δe=ek+1−ek=2nλ
若 n1<n2>n3 或 n1>n2<n3,则存在半波损失,棱边是暗纹,反之则棱边为明纹。
条纹间隔:
l=sinθΔe=2nsinθλ≈2nθλ=2ndDλ
光的衍射
衍射的分类:
- 菲涅耳衍射:光源、障碍物、接受屏中两者之间的距离为有限远。
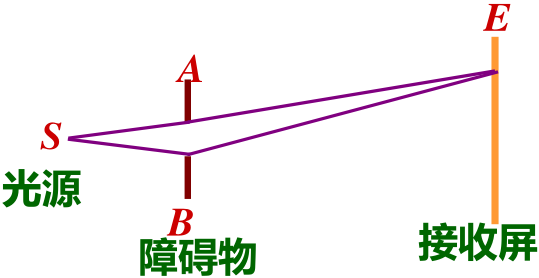
- 夫琅禾费衍射:光源、障碍物、接受屏之间的距离都为无穷远,且单缝的些许移动对衍射图样无影响。
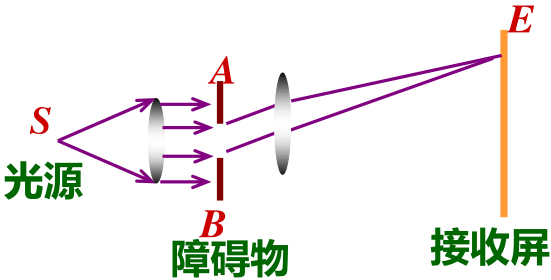
夫琅禾费单缝衍射
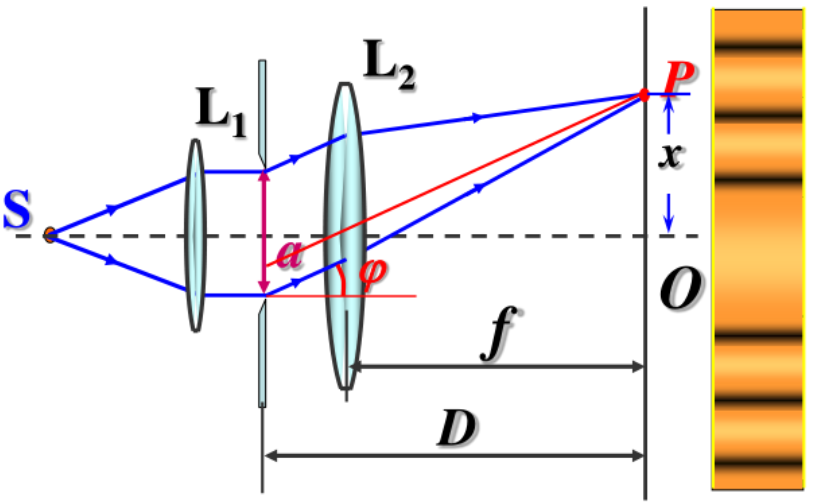
特点: 中央明纹宽度很大,其它各级明纹的宽度较小,且强度随级数增高而递减。
明暗条纹的条件: 使用半波带法。
δm=asinφ=⎩⎨⎧0±2k2λ±(2k+1)2λ中央明纹暗纹明纹 sinφ≈tanφ=fxk
半波带的数量 N=λ2asinφ.
条纹宽度: 中央明纹的半角宽度 φ≈sinφ=aλ,所以线宽度为
x0=2ftanφ≈2fsinφ=2faλ
其它明纹的宽度是中央明纹宽度的 21 倍,即
x=faλ
光栅衍射
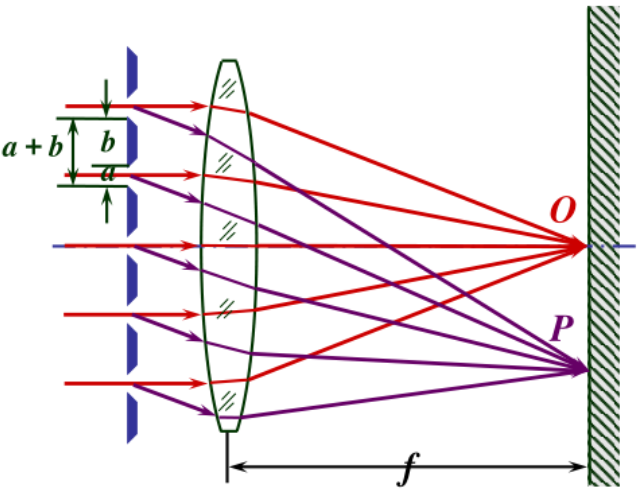
光栅(grating): 由大量等宽等间距平行狭缝组成的光学元件,分为反射光栅和透射光栅,a+b 称作光栅常量。
特点: 明纹亮度增加而条纹变细,且互相分得更开,在明纹之间形成大片暗区。
主极大明纹条件:
正入射光栅方程:
(a+b)sinφ=±kλ
斜入射光栅方程:
(a+b)(sinθ±sinφ)=±kλ
最高级次(φ=2π):需要向下取整
kmaxkmax=λa+b=λ(a+b)(sinθ+1)
极小(暗条纹)条件:(N 为狭缝数目)
(a+b)sinφ=±Nk′λ(k′=Nk,k′=0)
次极大明纹: 两暗条纹之间应为明条纹,故两主极大明纹间有 N−1 条暗纹,N−2 条明纹,其强度相比主极大明纹要小得多。
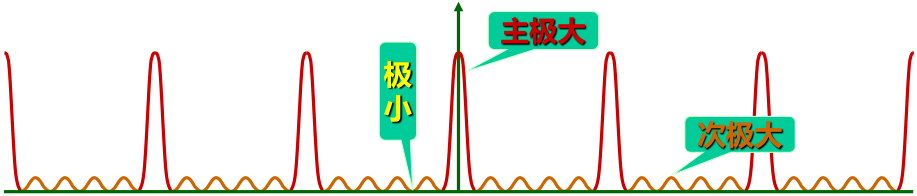
缺级现象: 当多缝光束干涉的主极大恰好与单缝衍射的极小位置重合时,该极主极大将在屏幕上消失的现象,即 φ 同时满足
{(a+b)sinφ=kλasinφ=k′λ
此时 (a+b)/a 为整数比,有
k=aa+bk′(k′=1,2,3,⋯)
光栅光谱: (a+b) 一定时,λ 不同,条纹在屏上位置不同。白光入射时,除中央条纹为白色明条纹外,其余各级明纹将按由紫到红的顺序依次分开,形成彩色光带对称地排列在中央明纹两侧,这个现象就称为光的色散。
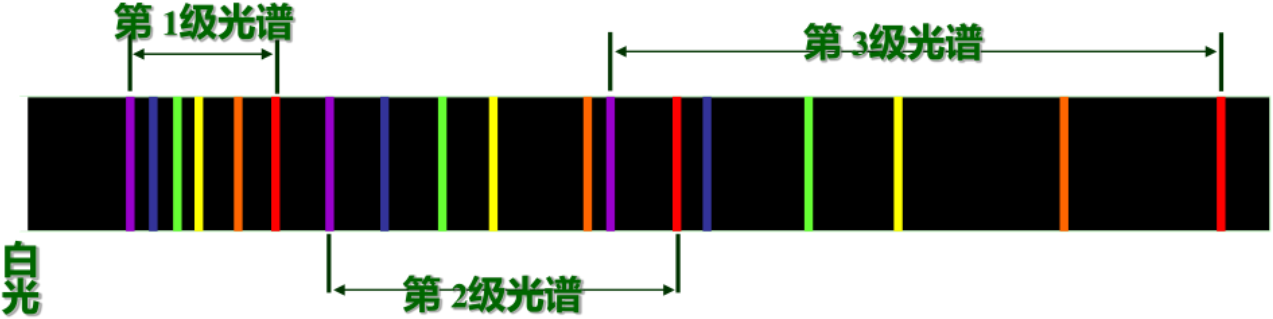
求某一级光谱的线宽度:
Δx=f⋅(tanφ1−tanφ2)
角宽度(张角):
Δφ=φ1−φ2=arcsin(a+bkλ1)−arcsin(a+bkλ2)
若 sinφ1>1,说明不存在完整光谱,则这一部分光谱的张角为
Δφ=2π−φ2








































