离散数学（二）：图论、数论与代数结构

图与网络

图的基本概念

设 $P$ 是一系列节点（node） 组成的非空集合，$L$ 是连接这些点中不同点对的边（edge） 集合，则 $P$ 和 $L$ 可以组成一张图（graph），记作 $G=(P,L)$。我们用 $P(G)$ 表示 $G$ 的 （节）点集，用 $L(G)$ 表示 $G$ 的边集。

设 $l\in L(G)$，并假设 $l$ 是连接 $G$ 中的点 $u,v$ 的边，则称 $u,v$ 是 $l$ 的端点，并称 $u$ 与 $v$ 相邻，在不引起混淆的情况下，可将 $l$ 记为 $uv$；若 $l_1,l_2\in L(G)$，且 $l_1$ 和 $l_2$ 拥有公共的端点，则称边 $l_1$ 与 $l_2$ 相邻。节点 $v$ 所所拥有的边的个数称作节点的度（node degree），记作 $\deg(v)$。

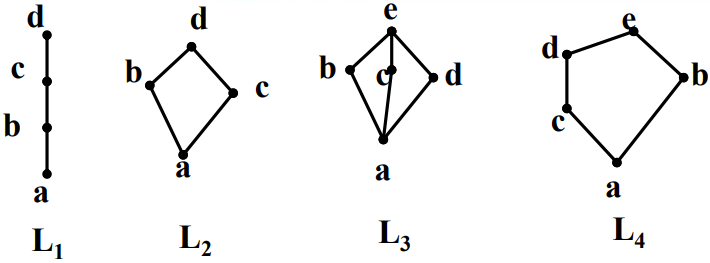
有限图（finite graph）： 由有限个点所组成的图（$P$ 为有限集）。
简单图（simple graph）： 任意一对不同点之间最多有一条边的图。
多重图（simple graph）： 任意一对不同点之间有多条平行边的图。
无向图（multigraph）： 允许有平行边和反身边的图。
空图/零图（empty/null graph）： 没有任何边的图（$L(G)=\emptyset$）。
平凡图（trivial graph）： 仅有一个节点的图。
完全图（complete graph）： 任意两点之间都有边的图。

补图（complementary graph）：
设 $G,H$ 是两个有限图，如果 $P(G)=P(H)$，并且对 $G$ 中相邻的两点 $u,v$，在 $H$ 中不相邻，则称 $G$ 与 $H$ 互为补图，记作 $G=\overline H$。即 $G$ 的补图是从其对应的完全图中删除 $G$ 拥有的边所剩余的图。

子图（subgraph）：

• 设图 $G,H$，若 $P(H)\subseteq P(G),L(H)\subseteq L(G)$，则称 $H$ 为 $G$ 的子图，$G$ 为 $H$ 的母图（supergraph）。
• 若 $H$ 为 $G$ 的子图，并且 $P(H)=P(G)$，则称 $H$ 为 $G$ 的生成子图（spanning subgraph，或称为支撑子图）。
• 若 $H$ 为 $G$ 的 子图，并且对 $P(H)$ 任意两个在 $H$ 中相邻的点，它们在 $G$ 中也相邻，则称 $H$ 为点集 $P(H)$ 在 $G$ 中诱导出的子图（induced subgraph）。即 $H$ 是 $G$ 删除某些点后得到的。

图的同构（graph isomorphism）：
设图 $G,H$，若存在 $P(G)$ 到 $P(H)$ 的双射 $\sigma$，使对任意的 $u,v\in P(G)$，$u$ 与 $v$ 在 $G$ 中相邻当且仅当 $\sigma(u)$ 与 $\sigma(v)$ 在 $H$ 中相邻，则称图 $G$ 与 $H$ 是同构的。我们一般将同构的图看作是同一个图。

有向图（directed graph）：

• 若边所对应的点对 $(u,v)$ 有序，则称其为有向边或弧（arc），所形成的图称为有向图，记作 $G=(P,A)$。弧的起点 $u$ 称为头（head），终点 $v$ 称为尾（tail），头和尾都是同一点的弧称为反身弧（reflexive arc）。

• 在有向图中，点 $v$ 作为图中弧的终点的次数之和称为点 $v$ 的入度（in-degree），记作 $\deg_+(v)$；点 $v$ 作为图中弧的起点的次数之和称为点 $v$ 的出度（out-degree），记作 $\deg_-(v)$，出度和入度满足

$$\deg(v)=\deg_+(v)+\deg_-(v)$$

• 若 $G$ 中一点 $v$ 的出度和入度皆为 0，则称点 $v$ 为孤立点；若 $G$ 中每点都有有限且相等的出度和入度，则称 $G$ 为平衡图（balanced graph）。

• 设有向图 $G,H$，若 $P(H)\subseteq P(G),A(H)\subseteq A(G)$，则称 $H$ 为 $G$ 的有向子图，$G$ 为 $H$ 的母图（supergraph）。

• 将有向图 $G$ 删去弧的方向、反身边和平行边后得到的图称为图 $G$ 的基图（base graph）。

图的表示法

关联矩阵（incidence matrix）：
设 $G=(P,L)$ 是有限图，集合 $P$ 的元素个数为 $m$，集合 $L$ 的元素个数 $|L|=n$，不妨设 $P(G)=\{v_1,\cdots,v_m\}$，$L(G)=\{l_1,\cdots,l_n\}$，则矩阵 $\bm M(G)=[a_{ij}]$ 称作 $G$ 的关联矩阵，其中

$$a_{ij}=\begin{cases} 0,&v_i\ \text{不是}\ l_j\ \text{的端点}\\ 1,&v_i\ \text{是}\ l_j\ \text{的端点} \end{cases}$$

邻接矩阵（adjacency matrix）：
设 $G=(P,L)$ 是有限图，集合 $P$ 的元素个数 $|P|=m$，不妨设 $P(G)=\{v_1,\cdots,v_m\}$，则矩阵 $\bm A(G)=[b_{ij}]$ 称作 $G$ 的邻接矩阵，其中

$$b_{ij}=\begin{cases} 0,&v_i\ \text{与}\ v_j\ \text{不相邻}\\ 1,&v_i\ \text{与}\ v_j\ \text{相邻} \end{cases}$$

定理 1（握手定理）： 设 $G=(P,L)$ 是有限图，则

$$\sum_{v\in P(G)}\deg(v)=2|L|$$

证明：

设 $\bm M(G)$ 是 $G$ 的关联矩阵，因为 $G$ 中某点 $v$ 的度 $\deg(v)$ 恰是 $\bm M(G)$ 中代表点 $v$ 那一行中 1 的个数，所以

$$\sum_{v\in P(G)}\deg(v)=M(G)\ \text{中}\ 1\ \text{的个数}$$

而 $\bm M(G)$ 中每列恰有两个 1，$\bm M(G)$ 共 $|L|$ 列，因此 $\bm M(G)$ 中 1 的个数为 $2|L|$，所以

$$\sum_{v\in P(G)}\deg(v)=2|L|$$

定理 2： 任一有限图中，奇数度的点的个数为偶数。

证明：

设 $S_1,S_2$ 分别是图 $G$ 中具有奇数度的点和具有偶数度的点的集合，则由握手定理可得

$$\sum_{v\in S_1}\deg(v)+\sum_{v\in S_2}\deg(v)=2|L|$$

为偶数。又因为 $\sum_{v\in S_2}\deg(v)$ 为偶数，所以 $\sum_{v\in S_1}\deg(v)$ 也为偶数，所以 $S_1$ 具有偶数个元素。

路与连通性

设图 $G$，$v,v'$ 是 $G$ 中两点，由 $G$ 中的点组成的序列 $(v_0,v_1,\cdots,v_n)$ 称为从 $v$ 到 $v'$ 的长度为 $\bm n$ 的路（walk），这条路中有 $n+1$ 个允许重复的点，并且

1. $v_0=v,v_n=v'$；
2. $v_i$ 与 $v_{i+1}$ 相邻，$0\leq i<n$.

回路（circuit）： 起点 $v_0$ 和终点 $v_n$ 重复的路，其长度不小于3。
回环（cycle）： 除了起点 $v_0$ 和 $v_n$ 重复以外，没有其它重复点的回路。
简单路（simple path）： 没有任何重复点和边的路。

设图 $G=(P,L)$，若从 $G$ 中两点 $u$ 到 $v$ 有一条路，则称 $u$ 与 $v$ 是相连的（connected）。我们一般规定，一个点与其自身是相连的。

$G$ 中两点之间的相连关系是一个等价关系，在此等价关系下，集合 $P(G)$ 可以分成一些等价类，设为 $S_0,\cdots,S_i,\cdots$，每一个 $S_i$ 和 $G$ 中所有以 $S_i$ 中的点为端点的边一同组成 $G$ 的一个子图 $G_i$，称为 $G$ 的一个连通分量（connected component），用 $W(G)$ 表示图 $G$ 的连通分量数。

所谓连通分量，就是自己内部连通但与整个图的其他部分不连通的子图。

如果图 $G$ 中仅有一个连通分量，则称图 $G$ 具有连通性（connectivity），称作连通图（connected graph），并且此时 $G$ 中任意两点都是相连的。

定理 1： 若图 $G$ 是不连通的，则 $G$ 的补图 $\overline G$ 是连通的。

证明（直接使用定义）：

设图 $G$ 的连通分量为 $G_1,G_2,\cdots,G_k\ (k\geq 2)$，任取 $G$ 中的两个点 $u,v$ 有如下两种情况：

1. $u,v$ 分别属于两个不同的连通分量，则 $uv$ 是 $\overline G$ 的边，因此，$\overline G$ 中存在点 $u$ 到点 $v$ 的路。
2. $u,v$ 属于同一个连通分量，则在另一个连通分量中取点 $w$，于是 $uw$ 和 $vw$ 都是 $\overline G$ 中的边，$\overline G$ 中存在点 $u$ 到点 $v$ 的路。

综上所述，$\overline G$ 是连通的。

定理 2： 设 $G=(P,L)$ 是有限图， $P(G),L(G)$ 的元素个数分别为 $m,n$，如果 $n>C_{m-1}^2$，则 $G$ 是连通的。

证明（反证法）：

假设此时 $G$ 不连通，则将 $G$ 中的一个连通分量作为子图记作 $G_1$，剩余的部分记作 $G_2$，并设 $P(G_1)$ 的元素个数为 $m_1$，$P(G_2)$ 的元素个数为 $m_2$，则

$$1\leq m_1,\quad m_2<m,\quad m_1+m_2=m$$

于是

$$\begin{aligned} n\leq m_1\frac{m_1-1}{2}+m_2\frac{m_2-1}{2}&=\frac 1 2\left(m_1^2+m_2^2-m_1-m_2\right)\\ &=\frac 1 2\left[(m_1+m_2)^2-2m_1m_2-(m_1+m_2)\right]\\ &=\frac 1 2\left(m^2-m-2m_1m_2\right) \end{aligned}$$

因为 $(m_1-1)(m_2-1)\geq 0$，所以有

$$\begin{aligned}m_1m_2-(m_1+m_2)+1&\geq 0\\m_1m_2&\geq m-1\end{aligned}$$

则

$$\begin{aligned} n\leq\frac 1 2\left[m^2-m-2(m-1)\right]&=\frac 1 2\left(m^2-3m+2\right)\\ &=\frac 1 2(m-1)(m-2)\\ &=C_{m-1}^2 \end{aligned}$$

产生矛盾，故原命题得证。

设有向图 $G=(P,A)$，如果弧序列 $(e_1,\cdots,e_n)$ 满足

1. $e_i\in A(G),\ i=1,2,\cdots,n$；
2. $v$ 是 $e_1$ 的起点，$v'$ 是 $e_n$ 的终点；
3. $e_k$ 的终点是 $e_{k+1}$ 的起点 $(1\leq k\leq n-1)$

则该弧序列称为 $G$ 的从 $v$ 到 $v'$ 的长度为 $n$ 的有向路（directed walk）。

对 $G$ 中任意两点 $v,v'\ (v\neq v')$，如果都有从 $v$ 到 $v'$ 的有向路，则称 $G$ 是强连通（strongly connected） 的；若有向图 $G$ 删去方向、反身边、平行边后得到的基图是连通的，则称图 $G$ 是弱连通（weakly connected） 的。

对于 $r\in P(G)$，如果对 $G$ 中任意一点 $v\ (v\neq r)$，都有从 $v$ 到 $r$ 的有向路，则称 $r$ 为 $G$ 的根（root）。

强连通图的每一点都是根。

树的基本定理

引理： 设 $G$ 是至少有一条边的有限图，且无回路，则 $G$ 至少有一点只相邻于另一点，即 $G$ 至少有一点度数为 1。

证明：

因为 $G$ 至少有一条边，所以 $G$ 有一点 $v_1$ 必有相邻点 $v_2$，若 $v_2$ 度数为 1，则 $v_2$ 即为所求的点；若 $v_2$ 度数大于 1，令 $v_3$ 为 $v_2$ 的不同于 $v_1$ 的相邻点。

以此类推，对于 $k\geq 2$，点 $v_k$ 有两种可能性：

1. $v_k$ 只与 $v_{k-1}$ 相邻，$v_k$ 即为所求的点；
2. $v_k$ 相邻于 $v_{k+1}\neq v_{k-1}$.

于是得 $v_1,v_2,\cdots,v_{k-1},v_k,v_{k+1},\cdots$，因为 $G$ 无回路，所以这一串点不会产生重复，又因为 $G$ 是有限图，故上述过程必然会在有限步内停止，从而引理得证。

由该引理，我们可以引出树与森林的概念：

定义： 设图 $G=(P,L)$，如果 $G$ 没有回路，则 $G$ 可以被称作森林（forest）；如果 $G$ 同时还是连通图，则 $G$ 可以被称作树（tree）。树中节点的度为它的子节点的个数（拥有子树的数目），度数为 0 的节点称作树叶（leaf），度数不为 0 的节点称作分支点（branch）。

对于图 $G=(P,L)$ 而言，以下命题等价成立：

1. $G$ 是树。
2. $G$ 是连通图，并且删去 $G$ 的任意一边，所得之图都不连通。
3. 对 $G$ 中任意不相同的两点 $v,v'$，恰有一条从 $v$ 到 $v'$ 的简单路。
4. 当 $|P|=n$ 时，$G$ 不含回路，且有 $n-1$ 条边。
5. 当 $|P|=n$ 时，$G$ 是连通图，且有 $n-1$ 条边。

推论： 任意有限连通图必有一生成子图是树，此生成子图称作母图的生成树（spanning tree，或称为支撑树）。若 $G'$ 是有限图 $G$ 的生成树，$vv'$ 为 $G$ 边，且 $vv'$ 不在 $G'$ 中，则 $G'$ 添上边 $vv'$ 后必有回路。

有向树（directed tree）： 如果有向图 $G$ 中有一点 $r$ 满足

1. $r$ 是图 $G$ 的根
2. $r$ 不是任何弧的起点；
3. $G$ 中每一点 $v\ (v\neq r)$ 都恰是一条弧 $e$ 的起点；

则称图 $G$ 为有向树。

有向树具有如下性质：

1. 有向树中每一点 $v\ (v\neq r)$ 到 $r$ 恰有一条有向路。
2. 有向树中没有有向回路。
3. 有向树中两点间最多有一条弧。

转化定理： 对有向树 $G$，若无视其各弧之方向，则得一树 $G_0$；反之，若 $G_0$ 为树，可选取任一点作根，并适当指定各边之方向，则得一有向树 $G$.

图论基本算法

加权图与 Dijkstra 算法

对于有限图 $G=(P,L)$，如果对 $L(G)$ 中每一条边都规定一个实数 $w(l)$ 附在其上，则称 $G$ 为加权图（weighted graph），称 $w(l)$ 为边 $l$ 的权重（weight）。

我们规定点与自身之间的权为 0，两个没有共享边的点之间的权为无穷 $\infty$.

在一张加权图 $G$ 中，任意两点 $u,v$ 之间都可能有多条路，在这些路中，所带的权重之和最小的那条就称作图中从 $u$ 到 $v$ 的最短路，这条最短路所带的权和称作从 $u$ 到 $v$ 的距离，记作 $d(u,v)$，即

$$d(u_0,S')=\min_{v\in S'}\{d(u_0,v)\},\quad(u_0\subseteq S\subseteq P,\ S'=P-S)$$

并且

$$d(u_0,S')=\min_{u\in S\atop v\in S'}\{d(u_0,u)+w(u,v)\}$$

两点间的最短路一定是简单路。

接下来我们所要了解的 Dijkstra 算法，就是一种用来求两点间最短路及其距离的通用解法。

Dijkstra 算法的基本思路： 基于贪心算法和广度优先搜索，从起始点开始，每次遍历到始点距离最近且未访问过的顶点的邻接节点，找到局部最短路径，直至扩展到终点为止。

算法实现：

设加权有限图 $G=(P,L)$，

1. 初始化，令 $S=\{u_0\}$，$S'=P-S$，对 $S'$ 中每一点 $v$，令 $l(v)=w(u_0,v)$；
2. 找到 $u_i\in S'$，满足 $l(u_i)=\min\limits_{v\in S'}\{l(v)\}$；
3. 令 $S=S\cup\{u_i\}$，$S'=S'-\{u_i\}$，对 $S'$ 中每一点 $v$，计算

$$l(v)=\min_{v\in S'}\{l(v),l(u_i)+w(u_i,v)\}$$

4. 重复步骤 2 和 步骤 3，直到 $S=P$ 后，算法停止。

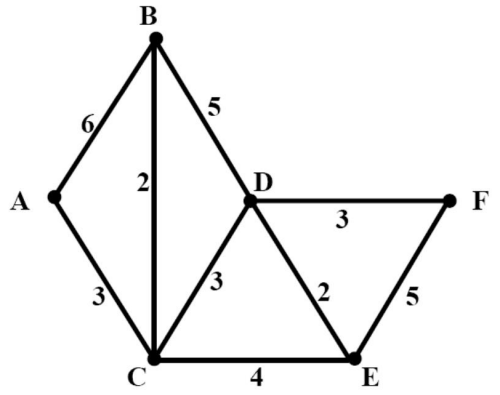
例：求下面加权图中 $A$ 点到其它各点的最短路及其距离：

解：

第一次遍历：

$$\begin{aligned} l(B)&=6\\ l(C)&=3\\ l(D)&=\infty\\ l(E)&=\infty\\ l(F)&=\infty \end{aligned}$$

$A$ 到 $C$ 的最短路为 $AC$，距离为 3；

第二次遍历：

$$\begin{aligned} l(B)&=\min\{l(B),l(C)+w(C,B)\}=\min\{6,3+2\}=5\\ l(D)&=\min\{l(D),l(C)+w(C,D)\}=\min\{\infty,3+3\}=6\\ l(E)&=\min\{l(E),l(C)+w(C,E)\}=\min\{\infty,3+4\}=7\\ l(F)&=\min\{l(F),l(C)+w(C,F)\}=\min\{\infty,3+\infty\}=\infty \end{aligned}$$

$A$ 到 $B$ 的最短路为 $ACB$，距离为 5；

第三次遍历：

$$\begin{aligned} l(D)&=\min\{l(D),l(B)+w(B,D)\}=\min\{6,5+5\}=6\\ l(E)&=\min\{l(E),l(B)+w(B,E)\}=\min\{7,5+\infty\}=7\\ l(F)&=\min\{l(F),l(B)+w(B,F)\}=\min\{\infty,5+\infty\}=\infty \end{aligned}$$

$A$ 到 $D$ 的最短路为 $ACD$，距离为 6；

第四次遍历：

$$\begin{aligned} l(E)&=\min\{l(E),l(D)+w(D,E)\}=\min\{7,6+2\}=7\\ l(F)&=\min\{l(F),l(D)+w(D,F)\}=\min\{\infty,6+3\}=9 \end{aligned}$$

$A$ 到 $E$ 的最短路为 $ACE$，距离为 7；

第五次遍历：

$$l(F)=\min\{l(F),l(E)+w(E,F)\}=\min\{9,7+5\}=9$$

$A$ 到 $F$ 的最短路为 $ACDF$，距离为 9。

最优树与 Kruskal 算法

设 $G$ 是加权连通图，带有最小权的生成树称作加权图 $G$ 的最优树（shortest path tree，SPT），最小生成树或 Huffman 树。

接下来我们所要了解的 Kruskal 算法，就是一种用来求加权连通图中最优树的通用解法。

Kruskal 算法的基本思路： 将连通网中所有的边按照权值大小做升序排序，从权值最小的边开始选择，只要此边不和已选择的边一起构成回路，就可以选择它组成最优树。对于 $n$ 个顶点的连通网，挑选出 $n-1$ 条符合条件的边，这些边组成的生成树就是最优树。

算法实现：

设加权连通图 $G=(P,L)$，

1. 在 $L(G)$ 中选取一个具有最小权值的边，记为 $l_1$，令 $T=\{l_1\}$；
2. 如果在 $L(G)-T$ 中存在 $l_i$，使得 $T\cup\{l_i\}$ 不产生回路，并且 $w(l_i)$ 最小，则令 $T=T\cup\{l_i\}$，重复此步骤；
3. 如果不存在这样的 $l_i$，则算法停止。
4. 最终得到的 $T=\{l_1,l_2,\cdots,l_n\}$ 即为 $G$ 的最优树。

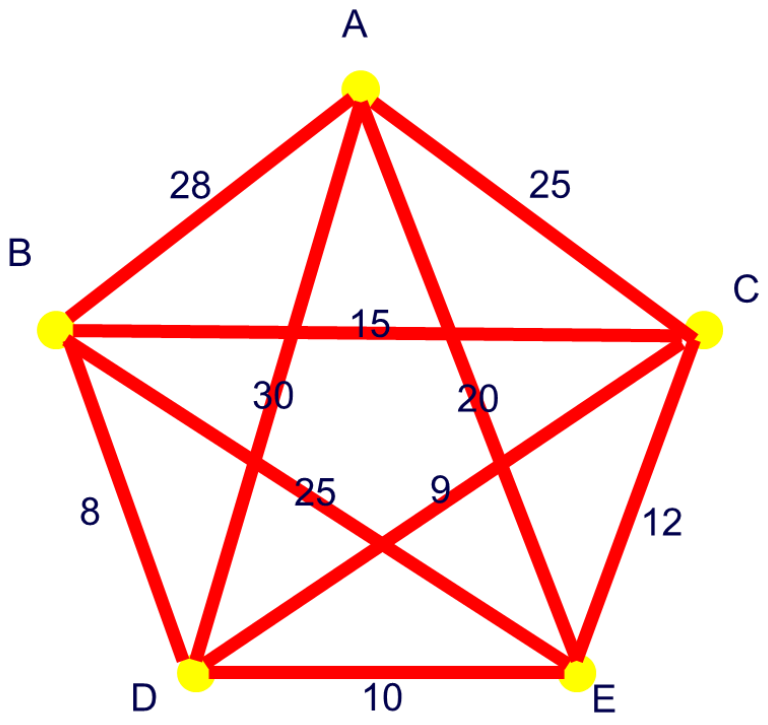
例：给出下面权图中最优树的权值：

$$BD(8),\quad CD(9),\quad DE(10),\quad AE(20)$$

故权值为 $8+9+10+20=47$.

欧拉图

设有向图 $G$，若图中一有向路 $(e_1,\cdots,e_n)$，其中 $e_n$ 的终点和 $e_1$ 的起点相同，并且 $G$ 中每条弧在此有向路中恰好出现一次，则称该有向路为欧拉路（Euler path），称该有向图 $G$ 为欧拉图（Euler graph）。

欧拉路实际上是一条封闭的一笔画路径。

若 $j>i$，则欧拉路形如：

$$(e_1,\cdots,e_i,\cdots,e_j,\cdots,e_n)$$

其中 $(e_i,e_{i+1},\cdots,e_{j-1})$ 是从 $v$ 到 $v'$ 的有向路。

若 $i>j$，则欧拉路形如：

$$(e_1,\cdots,e_j,\cdots,e_i,\cdots,e_n)$$

其中 $(e_i,e_{i+1},\cdots,e_n,e_1,\cdots,e_{j-1})$ 是从 $v$ 到 $v'$ 的有向路。

结论：

1. 一有限平衡有向图，其弧数必有限。
2. 一有向图若存在欧拉路，则必平衡。
3. 一欧拉图若没有孤立点，则必强连通。

判定欧拉图的充要条件： 设 $G$ 是无孤立点的有限有向图，$G$ 为欧拉图的充要条件是 $G$ 为平衡图且具有连通性（强连通或弱连通）。

欧拉图与有向树的相互转化：

定理 1： 设 $G$ 是无孤立点的有限有向图，并且 $G$ 有一条欧拉路 $(e_1,\cdots, e_m)$，则

1. 令 $r$ 同时为 $e_1$ 的起点和 $e_m$ 的终点；
2. 对每个不同于 $r$ 的点 $v$，令 $e_v=e_i$，其中 $i=\max\{j\mid e_j\ \text{的起点为}\ v\}$.

于是，$G$ 的全部点和弧 $\{e_v\mid v\neq r\}$ 作成的有向图就是一个以 $r$ 为根的有向树。

定理 2： 设 $G$ 是有限平衡有向图，$G'$ 是 $G$ 的有向生成树，设 $G'$ 的根为 $r$，$e_1$ 是 $r$ 在 $G$ 中发出的任意一条弧，对从 $e_1$ 开始的任意一条有向路：$L=(e_1,\cdots,e_m)$，若满足：

1. 当 $j\neq k$ 时，$e_j\neq e_k$；
2. 只有当 $G$ 中由点 $v$ 发出的弧都出现在 $(e_1,\cdots,e_j)$ 中，$e_j$ 的起点才能为 $v$；
3. 只有当 $G$ 中由弧 $e_m$ 的终点发出的弧都已经在 $L$ 中出现过，$L$ 才会终止在 $e_m$.

则有向路 $L$ 是一条欧拉路。

哈密顿图

设有限图 $G=(P,L)$，$(v_1,\cdots,v_n)$ 是图中一条路，如果 $G$ 中每点恰在此路中出现一次，则称此路为哈密顿路（Hamiltonian path）；如果 $G$ 中除 $v_1$ 以外的每点都恰在此路中出现一次，则称此路为哈密顿回路（Hamiltonian circuit）；拥有哈密顿回路的图称为哈密顿图（Hamiltonian graph）。

显然，由 $n\ (m\geq 3)$ 个点构成的完全图 $K_n$ 是哈密顿图。

哈密顿路与欧拉路的区别：

1. 哈密顿路不考虑方向性；欧拉路考虑方向性.
2. 哈密顿路着眼于无重复地遍历图中各点；欧拉路着眼于无重复地遍历图中各弧。
3. 哈密顿路一定为简单路；欧拉路未必为简单有向路。

哈密顿路的性质：

1. 若图中存在度为 1 的点，则无哈密顿回路。
2. 若图中存在度为 0 的点，则既无哈密顿路，也无哈密顿回路。
3. 若图中存在度为 2 的点，且存在哈密顿回路，则以此点为端点的两条边均出现在此回路中。
4. 若图中存在度大于 2 的点，且存在哈密顿回路，则只使用以此点为端点的其中两条边。
5. 若图中有 $n$ 个点，则哈密顿路恰有 $n-1$ 条边，哈密顿回路恰有 $n$ 条边。
6. 哈密顿路为生成树，哈密顿回路为生成子图。

哈密顿图的必要条件： 如果图 $G=(P,L)$ 是哈密顿图，则对 $P(G)$ 的任一非空子集 $S$，都有

$$W(G-S)\leq|S|$$

证明：

设 $C$ 是 $G$ 中的哈密顿回路，显然，$C$ 是 $G$ 的生成子图，所以 $C-S$ 是 $G-S$ 的生成子图，有

$$L(C-S)\subseteq L(G-S)$$

因此

$$W(G-S)\leq W(C-S)$$

又因为 $C$ 是哈密顿回路，依次删去一点及与此点相邻的两条边每次最多只增加一个分支，所以

$$W(C-S)\leq|S|$$

故 $W(G-S)\leq|S|$.

我们主要用该必要条件的逆否命题来判断非哈密顿图，即：若在图 $G$ 中删去 $n$ 个点及与之相连的边，所得图的分支数大于 $n$，则 $G$ 不是哈密顿图。

哈密顿图的充分条件与相关推论：

定义 1： 设图 $G$ 是非哈密顿图，若在 $G$ 中增加任意一条边 $l$，$G\cup\{l\}$ 是哈密顿图，则称 $G$ 为极大非哈密顿图。

定理 1： 设有限图 $G=(P,L)$，令 $\gamma=|P(G)|$，$\delta$ 表示 $G$ 中点的最小度数，若 $\gamma\geq 3$ 且 $\delta\geq\dfrac\gamma 2$，则 $G$ 是哈密顿图。

定理 2： 设有限图 $G$，$uv$ 是 $G$ 中不相邻的两点，且满足

$$\deg(u)+\deg(v)\geq\gamma$$

则 $G$ 是哈密顿图的充要条件是 $G\cup\{uv\}$ 是哈密顿图。

定义 2： 设有限图 $G=(P,L)$，反复连接 $G$ 中不相邻并且度数之和不小于 $|P|$ 的点对，直到没有这样的点对为止，最后得到的图称为 $G$ 的闭合图（closure of a graph），记作 $C(G)$.

有限图的闭合图是唯一确定的。

定理 3： 有限图 $G$ 是哈密顿图的充要条件是其闭合图 $C(G)$ 是哈密顿图。

定理 2 可以用 定理 3 推得。

定理 4： 将有限图 $G$ 的各点的度按非降序排成的序列，称为 $G$ 的度序列（sequence of degrees），记作 $(\deg_1,\deg_2,\cdots,\deg_\gamma)$；如果不存在 $m\ (m<\dfrac\gamma 2)$，使得

$$\deg_m\leq m,\quad\deg_{\gamma-m}<\gamma-m$$

则 $G$ 是哈密顿图。

定义 3： 设 $G,H$ 是两个无公共点的有限图，将 $G$ 的每个点和 $H$ 的每个点都用边连接起来得到的图，称为 $G$ 与 $H$ 的连接图；由 $K_m,\overline{K_m},K_{n-2m}\ (1\leq m<\dfrac n 2)$ 连接起来构成的图记作 $C_{m,n}$，该图不是哈密顿图。

定理 5： 若有限图 $G=(P,L)\ (|P|\geq 3)$ 不能被任意一个 $C_{m,|P|}$ 通过增加点的度数得到，则 $G$ 是哈密顿图。

推论： 由 $n$ 个点组成的边数最多的非哈密顿图是 $C_{1,n}$，其边数为

$$|L|=\frac 1 2 (n-1)(n-2)+1$$

数论基础

整除性与辗转相除法

设 $a$ 和 $b$ 是任意整数，若存在整数 $c$，使得 $a=bc$，则称 $a$ 是 $b$ 的倍数（multiple），$b$ 是 $a$ 的因数（factor），此时 $a$ 能被 $b$ 整除，$b$ 能整除 $a$，记作 $b|a$.

任何整除都能整除 0，且规定 $0|0$；1 或 -1 可以整除任何整数。

对任意整数 $a$ 和 $b\ (b\neq 0)$，唯一存在一对整数 $q$ 和 $r$ 使得

$$a=qb+r,\quad 0\leq r<|b|$$

将 $q$ 称为商数（quotient），$r$ 称为 $a$ 被 $b$ 除的余数（remainder）。

若 $d$ 同时是 $a$ 和 $b$ 的因数，则称 $d$ 为 $a,b$ 的公因数（common factor）；若 $a,b$ 的任意公因数整除 $d$，则称 $d$ 为 $a,b$ 的最大公因数（greatest common factor，GCD），记作 $d=\gcd(a,b)$。

整除的基本性质：

1. 若 $a|b,b|c$，则 $a|c$.
2. 若 $a|b$，则 $a|bc$.
3. 若 $a|b,b|a$，则 $b=\pm a$.
4. 若 $a|b,b|c$，则 $a|b\pm c$.
5. 若 $a$ 整除 $b_1,\cdots,b_n$，$\lambda_i$ 为任意整数，则 $a|\lambda_1b_1+\cdots+\lambda_nb_n$.
6. 若在一等式中，除某项外，其余各项都是 $a$ 的倍数，则该项也是 $a$ 的倍数。
7. 设 $a=qb+c$，则 $a,b$ 的公因数与 $b,c$ 的公因数完全相同。
8. $\gcd(a,0)=\gcd(0,a)=|a|$.

辗转相除法（algorithm of division）：

辗转相除法是一个常用于求两个数的最大公因数的算法，它的基本思路如下：

若 $b|a$，则由定义易见，$b$ 就是 $a,b$ 的最大公因数；同理，若 $a|b$，则 $a$ 就是 $a,b$ 的最大公因数；
若 $a$ 和 $b$ 无法相互整除，因为任何数都可以整除 0，所以 $a\neq 0,b\neq 0$；以 $b$ 除 $a$ 得商 $q_1$ 和余数 $r_1$，再以 $r_1$ 除 $b$ 得商 $q_2$ 和余数 $r_2$，之后 $r_2$ 除 $r_1$ 得商 $q_3$ 和余数 $r_3$，如此递推可以得到以下各式：

$$\begin{cases} a=q_1b+r_1\\ b=q_2r_1+r_2\\ r_1=q_3r_2+r_3\\ \cdots\\ r_{k-2}=q_kr_{k-1}+r_k\\ \cdots\\ r_{n-2}=q_nr_{n-1}+r_n\\ r_{n-1}=q_{n+1}r_n \end{cases}$$

其中 $r_n$ 是最后一个非 0 余数，即为 $a,b$ 的最大公因数。

由性质 7 可得，$a,b$ 的公因数和 $b,r_1$ 的公因数完全相同，$b,r_1$ 的公因数和 $r_1,r_2$ 的公因数完全相同……如此类推可得：$a,b$ 的公因数和 $r_{n-1},r_n$ 的公因数完全相同。

又因为 $r_n|r_{n-1}$，所以 $r_n$ 是 $r_{n-1},r_n$ 的最大公因数，因而 $r_n$ 也是 $a,b$ 的最大公因数。

任意两个整数 $a,b$ 都有最大公因数，且可以表示为 $a,b$ 的倍数和，即

$$\gcd(a,b)=sa+tb$$

其中 $s,t$ 都是整数。使用辗转相除法可以求出这两个系数，主要公式如下：

$$S_0=0,\quad S_1=1,\quad T_0=1,\quad T_1=q_1\\ S_k=q_kS_{k-1}+S_{k-2}\\ T_k=q_kT_{k-1}+T_{k-2}$$

若 $r_n$ 即最大公因数，则

$$\gcd(a,b)=(-1)^{n-1}S_na+(-1)^nT_nb$$

互质性与质数相关定理

若 $a,b$ 除了 $\pm 1$ 以外没有其它公因数，则称 $a$ 和 $b$ 互质（coprime）。

$a$ 和 $b$ 互质的充要条件是 $a,b$ 的最大公因数为 1；
$\pm 1$ 与任何整数（包括 0）都互质。

定理 1： 若 $a$ 和 $b$ 互质，而 $a|bc$，则 $a|c$.

证明：

因为 $a,b$ 互质，所以有 $s,t$ 使得 $sa+tb=1$，从而

$$sac+tbc=c$$

因为 $a$ 能整除左边每一项，所以 $a|c$.

定理 2： 若 $a$ 和 $b_1,b_2,\cdots,b_n$ 都互质，则 $a$ 与它们的乘积 $b_1b_2\cdots b_n$ 也互质。

证明：

对 $i=1,2,\cdots,n$ 有 $s_i,t_i$ 使得

$$s_ia+t_ib_i=1$$

把所有这 $n$ 个式子乘起来，得

$$Sa+Ta_1a_2\cdots a_n=1$$

故由定义可得，$a$ 与 $b_1b_2\cdots b_n$ 互质。

定理 3： 若 $m_1,m_2,\cdots,m_k$ 两两互质且都整除 $a$，则 $m_1m_2\cdots m_k|a$.

质数与合数：

一个正整数，如果不等于 1 且除了自己和 1 以外没有其它正因数，则称其为质数（或素数，prime number），否则称为合数（composite number）。

两个质数互质的条件是无法互相整除；任意两个不同的质数互质。

算术基本定理： 任何一个大于 1 的自然数，如果其不为质数，都可以唯一分解成有限个质数的乘积。

证明：

存在性：利用数学归纳法，设正整数 $n,a\ (n\geq 2)$，

1. $n=2$ 时，2 为质数，显然成立。
2. 假设 $n<a$ 时，$n$ 可以写为有限个质数的乘积。
3. $n=a$ 时，若 $a$ 是质数，则 $n$ 也是质数，存在性成立；若 $a$ 不是质数，则 $a$ 有因数 $b,c$，并且令 $1<c<b<a$；由归纳假定可得，$b,c$ 都可以写成质数的乘积，且 $a=bc$，所以 $n=a$ 也可以写成质数的乘积，存在性成立。

唯一性：利用反证法，设

$$n=p_1\cdots p_h=q_1\cdots q_k$$

其中 $p_1,\cdots,p_h$ 和 $q_1,\cdots,q_k$ 都是质数，并且为根本不同的两列数。因为

$$\frac{p_1}{q_1\cdot(q_2\cdots q_k)}=p_2\cdots p_h$$

所以，由定理 1可得 $p_1|q_1$ 或 $p_1|q_2\cdots q_k$，又由 $p,q$ 全为质数，可得 $p_1=q_1$ 或 $p_1=q_i\ (i=2,\cdots,k)$.

以上任意一种情况，都可以将原式左右两端同消去一个数，如此递推，最终可知 $p_1,\cdots,p_h$ 和 $q_1,\cdots,q_k$ 除了次序以外完全相同，与假设产生矛盾，唯一性得证。

Euclid 定理： 质数无穷多。

证明：利用反证法，假设质数只有有限个，设为 $p_1,\cdots,p_n$，则对于

$$N=p_1p_2\cdots p_n+1$$

$p_1,\cdots,p_n$ 无法整除 $N$，否则存在 $p_i|1\ (i=1,\cdots,n)$，即 $p_i=1$，与 $p_i$ 为质数产生矛盾；所以 $N$ 无质因数，可得 $N$ 为质数，与质数仅有 $p_1,\cdots,p_n$ 产生矛盾，故可证质数无穷多。

同余式与剩余系

设任意整数 $a,b$ 和非零整数 $m$，若 $m|a-b$，则称 $a,b$ 对模 $m$ 同余（congruence），记作 $a\equiv b\pmod m$；同余为整除的另一种表示法，$a\equiv 0\pmod m$ 表示的即为 $m|a$.

在讨论同余时，我们一般假定 $m$ 是正整数。

$a\equiv b\pmod m$ 当且仅当 $m$ 除 $a$ 和 $b$ 所得的余数相同。

同余的基本性质：

1. $a\equiv a$.
2. 若 $a\equiv b$，则 $b\equiv a$.
3. 若 $a\equiv b$，$b\equiv c$，则 $a\equiv c$.
4. 若 $a\equiv b\pmod m$，$c\equiv d\pmod m$，则 $a\pm c\equiv b\pm d\pmod m$，$ac\equiv bd\pmod m$.
5. 若 $a\equiv b\pmod m$，则对任意整数 $k$，有 $a\pm k\equiv b\pm k\pmod m$.
6. 若 $a+b\equiv c\pmod m$，则 $a\equiv c-b\pmod m$.
7. 若 $a\equiv b\pmod m$，则对任意整数 $k$，有 $ka\equiv kb\pmod m$.
8. 若 $a\equiv b\pmod m$，则对 $n\geq 0$，有 $a^n\equiv b^n\pmod m$.
9. 若 $ac\equiv bc\pmod{mc}$ 且 $c\neq 0$，则 $a\equiv b\pmod m$.
10. 若 $ac\equiv bc\pmod m$，且 $c$ 和 $m$ 互质，则 $a\equiv b\pmod m$.
11. 若 $ac\equiv bc\pmod m$，且 $\gcd(c,m)=d$，则 $a\equiv b\left(\bmod\dfrac m d\right)$.
12. 若 $p$ 为质数，$c\not\equiv 0\pmod p$，而 $ac\equiv bc\pmod p$，则 $a\equiv b\pmod p$.
13. 设 $p(x)$ 是整系数多项式，$x$ 和 $y$ 是整数变量，则由 $x\equiv y\pmod m$ 可得

$$p(x)\equiv p(y)\pmod m$$

剩余系：

同余是一种等价关系，我们可以把所有整数按照模 $m$ 同余的关系分为等价类，每一个等价类称为模 $m$ 的一个剩余类（residue class）。同一个剩余类中的数互相同余。

因为以 $m$ 去除任意整数，可能得到的余数恰有 $0,1,\cdots,m-1$ 这 $m$ 个数，所以模 $m$ 共有 $m$ 个剩余类。

从模 $m$ 的每个剩余类中任意取出一个数作为代表，得到 $m$ 个数，例如 $r_1,r_2,\cdots,r_m$，称这 $m$ 个数形成一个完全剩余系（complete system of residues）。

含有整数变量的同余式称作同余方程；诸如 $ax\equiv b\pmod m$ 这种形式的同余方程称作一次同余方程，类似地，$a_2x^2+a_1x\equiv b\pmod m$ 称作二次同余方程。

一次同余方程解的个数：

若 $\gcd(a,m)=1$，则 $ax\equiv b\pmod m$ 只有唯一解；

若 $\gcd(a,m)=d>1$，则

1. $d$ 可以整除 $b$，则 $ax\equiv b\pmod m$ 有 $d$ 个解；
   令 $\alpha$ 为 $\dfrac a d x\equiv\dfrac b d\left(\bmod\dfrac m d\right)$ 的解，则这 $d$ 个解分别为

$$\alpha,\alpha+\frac m d,\alpha+\frac{2m}d,\cdots,\alpha+\frac{(d-1)m}d$$

2. $d$ 无法整除 $b$，则 $ax\equiv b\pmod m$ 无解。

一次同余方程的解法：

法 1： 先使用辗转相除法，将互质的 $a$ 与 $m$ 的最大公因数 1 表示为 $a$ 和 $m$ 的倍数和的形式，即 $1=sa+tm$，然后取 $x=sb$，即可完成求解。

因为 $a$ 和 $m$ 互质，故存在 $s,t$ 使得 $sa+tm=1$，于是有 $sab+tmb=b$，若取模 $m$，则有 $sab+tmb=b\pmod m$.
取 $x=sb$，则 $sb$ 所在的剩余类中的数皆为解。

法 2： 利用同余的性质，使 $x$ 的系数变为 1，即可完成求解。

例：解 $103x\equiv 57\pmod{211}$.

解：因为 $211=103\times 2+5$，所以由同余的性质 7 可得

$$2\times 103x\equiv 2\times 57\pmod{211}$$

因为 $211x\equiv 0\pmod{211}$，所以由同余的性质 4 可得

$$211x-2\times 103x\equiv 0-2\times 57\pmod{211}$$

即

$$5x\equiv-114\equiv97\pmod{211}$$

又因为 $211=42\times 5+1$，所以由同余的性质 7 可得

$$42\times 5x\equiv 42\times 97\equiv 211\times 19+65\equiv 65\pmod{211}$$

再由同余的性质 5 可得

$$211x-42\times 5x\equiv 0-65\pmod{211}$$

即可求得 $x\equiv -65\pmod{211}$.

代数运算与代数系统

代数运算的定义

设 $S$ 是一个非空集合，称映射 $f : S \times S \rightarrow S$ 为 $S$ 的一个二元运算，即对 $S$ 中任意两个元素 $a, b$，可以确定 $S$ 中另一个元素 $f(a, b) = c$，常记为 $a * b = c$，这体现了代数运算的封闭性。

类似地，可以定义 $S$ 的 $n$ 元运算为 $f : S_n \rightarrow S$.

例：

• 加法和乘法是自然数集 $\N$ 上的二元运算；减法和除法不是 $\N$ 上的二元运算。
• 加法、减法和乘法是整数集 $\Z$ 上的二元运算；除法不是 $\Z$ 上的二元运算。
• 乘法、除法是非零实数集 $\R^*$ 上的二元运算；加法和减法不是 $\R^*$ 上的二元运算。
• 矩阵加法和乘法是 $n$ 阶实矩阵集合上的二元运算。
• 设非空集合 $S$，$\cap$ 和 $\cup$ 是 $S$ 的幂集 $\rho(S)$ 上的二元运算。
• $\vee$、$\wedge$、$\rightarrow$、$\leftrightarrow$ 是真值集合 ${ 0, 1 }$ 上的二元运算。
• 设非空集合 $A$，$M(A)$ 是 $A\rightarrow A$ 的所有双射构成的集合，则映射的乘积是 $M(A)$ 上的二元运算。

代数运算的性质

1. 交换律：
设 $*$ 是集合 $S$ 上的二元运算，如果对于 $S$ 中任意两个元素 $a, b$，都有等式

$$a * b = b * a$$

成立，则称运算 $*$ 满足交换律。

2. 结合律：
设 $*$ 是集合 $S$ 上的二元运算，如果对于 $S$ 中任意三个元素 $a, b, c$，都有等式

$$a * b * c = a * (b * c)$$

成立，则称运算 $*$ 满足结合律。

3. 幂等律：
设 $*$ 是集合 $S$ 上的二元运算，如果对于 $S$ 中任意元素 $a$，都有等式

$$a * a = a$$

成立，则称运算 $*$ 满足幂等律，称 $a$ 为关于运算 $*$ 的幂等元。

此时，对于任意正整数 $n$，满足 $a^n = a$.

4. 分配律：
设 $*$ 和 $+$ 是集合 $S$ 上的二元运算，如果对于 $S$ 中任意三个元素 $a, b, c$，都有等式

$$a * (b + c) = (a * b) + (a * c)\\ (b + c) * a = (b * a) + (c * a)$$

成立，则称运算 $*$ 对 $+$ 满足分配律。

满足分配律的 $*$ 未必满足交换律，两个等式不一定同时成立。

5. 吸收律：
设 $*$ 和 $+$ 是集合 $S$ 上的二元运算，如果对于 $S$ 中任意两个元素 $a, b$，都有等式

$$a * (a + b) = a\\ a + (a * b) = a$$

成立，则称运算 $*$ 和 $+$ 满足吸收律。

6. 消去律：
设 $*$ 是集合 $S$ 上的二元运算，如果对于 $S$ 中任意三个元素 $a, b, c$，满足

• 若 $a * b = a * c$，则 $b = c$；
• 若 $b * a = c * a$，则 $b = c$.

则称运算 $*$ 满足消去律。

例：

• 整数集 $\Z$ 上的加法和乘法都满足交换律和结合律；乘法对加法满足分配律，但加法对乘法不满足分配律；减法既不满足交换律，也不满足结合律；它们都不满足幂等律和吸收律。
• $n$ 阶实矩阵集合上的加法满足交换律和结合律；乘法满足结合律，但不满足交换律；它们都不满足幂等律和吸收律。
• 设 $\rho(S)$ 是非空集合 $S$ 的幂集，则 $\rho(S)$ 上的 $\cap$ 和 $\cup$ 满足交换律和结合律；$\cup$ 对 $\cap$ 和 $\cap$ 对 $\cup$ 都满足分配律，它们也都满足幂等律和吸收律；$\cap$ 和 $\cup$ 都不满足消去律。

代数系统的定义

设非空集合 $S$，$f_1, \cdots, f_n$ 是 $S$ 上的代数运算，把 $S$ 及其运算 $f_1, \cdots, f_n$ 作为一个整体，称为代数系统（algebra system），记作 $(S, f_1, \cdots, f_n)$.

例：设 $\Z$ 为整数集，$\Z_0$ 为偶数集，$\N$ 为自然数集，$+, \cdot$ 为数的加法和乘法，则 $(\Z, +)$，$(\Z, \cdot)$，$(\Z, +, \cdot)$，$(\Z_0, +)$，$(\Z_0, \cdot)$，$(\Z_0, +, \cdot)$，$(\N, +)$，$(\N, \cdot)$，$(\N, +, \cdot)$ 都是代数系统。

零元： 设 $*$ 是集合 $S$ 上的二元代数运算，若 $S$ 中存在元素 $\theta$，使得对于 $\forall a\in S$，都存在 $a * \theta = \theta$，$\theta * a = \theta$，则称 $\theta$ 是 $S$ 上关于运算 $*$ 的零元。

例：设 $\rho(S)$ 是非空集合 $S$ 的幂集，$\cap$ 和 $\cup$ 是 $\rho(S)$ 上的交运算和并运算，则 $\empty$ 是 $\rho(S)$ 上关于 $\cap$ 的零元，$S$ 是 $\rho(S)$ 上关于 $\cup$ 的零元。

群（Group）

群是一个带有某种运算的集合，这个运算如何表示并不重要，可以是加法和乘法，也可以是其他的运算。在群论中通常将运算符号省略不写，并不失一般性地称群中的运算为乘法。乘法群中的单位元通常写作$1$ 或 $e$，逆元通常写作 $a^{-1}$；加法群中的单位元通常写作 $0$，逆元通常写作 $-a$.

半群的定义

设非空集合 $G$，若 $\cdot$ 为 $G$ 上的二元代数运算，且满足结合律，则称该代数系统 $(G, \cdot)$ 为半群（semigroup）。

例：

• 设 $\Z$ 为整数集，$+, -, \cdot$ 为数的加法、减法和乘法，则 $(\Z, +)$，$(\Z, \cdot)$ 都是半群，$(\Z, -)$ 不是半群。
• 设 $\rho(S)$ 是非空集合 $S$ 的幂集，$\cap$ 和 $\cup$ 是 $\rho(S)$ 上的交运算和并运算，则 $(\rho(S), \cap)$ 和 $(\rho(S), \cup)$ 都是半群。

含有单位元的半群称为单位半群或独异点（monoid）。

例：设 $A$ 是一个非空集合，$A^A$ 是 $A$ 到 $A$ 的所有映射组成的集合。证明 $A^A$ 关于映射的乘积 “$\cdot$” 构成一个有单位半群。

证：

1. 因为 $A$ 非空，所以 $A^A$ 非空。
2. 运算满足封闭性和结合律：$\forall f, g \in A^A$，$f(g(x)) = (f \cdot g)(x)$ 且 $f \cdot g \in A^A$.
3. 存在单位元：恒等映射 $I_A(x) = x$，$f \cdot I_A = I_A \cdot f = f$.

群的定义与性质

设 $(G, \cdot)$ 为半群，如果满足下列条件，则称 $(G, \cdot)$ 为群（group）：

• 存在单位元：$G$ 中存在一个元素 $e$，使得对于 $G$ 中任意元素 $a$，都存在 $e \cdot a = a \cdot e = a$；
• 存在逆：对于 $G$ 中任意元素 $a$，都存在 $G$ 中的元素 $a^{-1}$，使得 $a \cdot a^{-1} = a^{-1} \cdot a = e$.

如果一个群包含的元素个数有限，则称其为有限群，否则称其为无限群。

例：

• 设 $\Z$ 为整数集，$+, \cdot$ 为数的加法和乘法，则 $(\Z, +)$ 为整数加法群，$(\Z, \cdot)$ 除了 $1$ 和 $-1$ 以外的元素都没有逆，不是群。
• 设 $\rho(S)$ 是非空集合 $S$ 的幂集，$\cap$ 和 $\cup$ 是 $\rho(S)$ 上的交运算和并运算，则 $(\rho(S), \cap)$ 除了 $S$ 以外的元素都没有逆，$(\rho(S), \cup)$ 除了 $\empty$ 以外的元素都没有逆，它们都不是群。

设 $S = \{ 0, 1, 2, \cdots, n - 1 \}$，$a, b$ 是 $S$ 中任意元素，$+, -$ 为数的加法和减法，规定 $S$ 上的运算 $\oplus$ 为

$$a \oplus b = \begin{cases} a + b, & a + b < n\\ a + b - n, & a + b \geq n \end{cases}$$

则 $(S, \oplus)$ 为群，称为模 $\bm{n}$ 的整数加法群。

模 $n$ 的整数加法群即所有模 $n$ 同余类中的整数集合，通过加法运算而构成的群。

群的单边定义： 满足下列条件的半群 $G$ 即可成为群：

• $G$ 中存在左单位元 $e_l$，满足 $\forall a \in G$，${e_l}a = a$；
• $G$ 任意元素存在左逆元，即 $\forall a \in G$，$\exists a^{-1} \in G$，$a^{-1} \cdot a = e_l$.

对于右单位元和右逆元也同样成立，但对于左单位元和右逆元或右单位元和左逆元不成立。

证明：

先证 $a \cdot a^{-1} = e_l$：

$$a^{-1} = e_l \cdot a^{-1} = (a^{-1} \cdot a) \cdot a^{-1}$$

设 $a^{-1}$ 的左逆元为 $b$，满足 $b \cdot a^{-1} = e_l$，则

$$\begin{aligned} b \cdot a^{-1} &= b \cdot ((a^{-1} \cdot a) \cdot a^{-1})\\ &= (b \cdot a^{-1}) \cdot (a \cdot a^{-1})\\ &= e_l \cdot (a \cdot a^{-1})\\ &= a \cdot a^{-1} \end{aligned}$$

再证 $a \cdot e_l = a$：

$$\begin{aligned} a \cdot e_l &= a \cdot (a^{-1} \cdot a)\\ &= (a \cdot a^{-}) \cdot a\\ &= 1 \cdot a = a \end{aligned}$$

例：设 $(G, \cdot)$ 是一个群，$u \in G$，定义 $a * b = a \cdot u^{-1} \cdot b, \ \forall a, b \in G$，证明 $(G, *)$ 是一个群。

证：

1. 因为 $u \in G$，所以 $G$ 非空。
2. 运算的封闭性：$\forall a, b \in G$，$a * b = a \cdot u^{-1} \cdot b \in G$.
3. 运算的结合律：$\forall a, b \in G$，满足

$$(a * b) * c = (a \cdot u^{-1} \cdot b) * c = a \cdot u^{-1} \cdot b \cdot u^{-1} \cdot c\\ a * (b * c) = a * (b \cdot u^{-1} \cdot c) = a \cdot u^{-1} \cdot b \cdot u^{-1} \cdot c$$

4. 存在左单位元：$\forall a \in G$，有 $u \in G$，使得 $u * a = u \cdot u^{-1} \cdot a = a$，单位元 $e = u$.
5. 存在左逆元：$\forall a \in G$，有 $(u \cdot a^{-1} \cdot u) \in G$，使得

$$(u \cdot a^{-1} \cdot u) * a = (u \cdot a^{-1} \cdot u) \cdot u^{-1} \cdot a = u$$

群的可除条件： 对任意 $a, b \in G$，满足下列可除条件的半群 $G$ 即可成为群：

• 存在 $x \in G$，使得 $x \cdot a = b$；
• 存在 $y \in G$，使得 $a \cdot y = b$.

证明：

在任意群中，取 $x = b \cdot a^{-1}, y = a^{-1} \cdot b$，即可得 $x \cdot a = b, a \cdot y = b$，所以在任意群中可除条件都成立。

任取 $c \in G$，令 $e$ 为满足 $x \cdot c = c$ 的 $x$，即 $e \cdot c = c$；对于任意 $a \in G$，存在 $y$ 使得 $c \cdot y = a$，故

$$e \cdot a = e \cdot (c \cdot y) = (e \cdot c) \cdot y = c \cdot y = a$$

所以 $G$ 中存在左单位元 $e$.

令 $a^{-1}$ 为满足 $x \cdot a = e$ 的 $x$，即 $a^{-1} \cdot a = e$，则 $G$ 中任意元素存在左逆。

再由群的单边定义可得 $G$ 为群。

定理： 单位元是群中唯一的幂等元。

证明：设 $(G, \cdot)$ 为群，其单位元为 $e$，显然 $e$ 是幂等元；设 $x$ 是 $G$ 中的幂等元，即 $x \cdot x = x$，则

$$x = 1 \cdot x = (x^{-1} \cdot x) \cdot x = x^{-1} \cdot (x \cdot x) = x^{-1} \cdot x = e$$

定理： 群中无零元。

证明：设 $(G, \cdot)$ 为群，其单位元为 $e$.

（1）当 $|G| = 1$ 时，将其唯一元素视为单位元，无零元。

（2）当 $|G| > 1$ 时，使用反证法：

• 假设 $\theta = e$，任取 $G$ 中元素 $x \neq \theta$，则 $x = e \cdot x = \theta \cdot x = \theta$，产生矛盾，所以 $\theta \neq e$；
• 假设 $(G, \cdot)$ 有零元 $\theta \neq e$，则对 $\forall x \in G$，都有 $x \cdot \theta = \theta \cdot x = \theta \neq e$，即不存在 $x \in G$，使得 $x \cdot \theta = \theta \cdot x = e$，即 $\theta$ 不存在逆元素，与 $G$ 是群产生矛盾。

综上所述，$G$ 中不存在零元。

定理： 群中消去律一定成立。

证明：设 $(G, \cdot)$ 为群，其单位元为 $e$，对于 $G$ 中任意三个元素 $a, b, c$：

（1）若 $a \cdot b = a \cdot c$，则

$$\begin{aligned} a^{-1} \cdot (a \cdot b) &= a^{-1} \cdot (a \cdot c)\\ (a^{-1} \cdot a) \cdot b &= (a^{-1} \cdot a) \cdot c\\ e \cdot b &= e \cdot c\\ b &= c \end{aligned}$$

（2）同理可证：若 $b \cdot a = c \cdot a$，则 $b = c$.

定理： 群的单位元 $e$ 是唯一的，群中任意元素的逆也是唯一的。

结论：

• $(a^{-1})^{-1} = a$
• $(a \cdot b)^{-1} = b^{-1} \cdot a^{-1}$
• $e^{-1} = e$

定理： 我们规定群中任意元素 $a^0 = e$，$a^{-n} = (a^n)^{-e}$，则对于任意整数 $m, n$，有

• 第一指数律 $a^m \cdot a^n = a^{m + n}$ 成立；
• 第二指数律 $(a^m)^n = a^{mn}$ 成立；
• 第三指数律 $(a \cdot b)^n = a^n \cdot b^n$ 一般不成立。

例：证明在偶数元的有限群中，方程 $x^2 = 1$ 有偶数个解。

证：方程 $x^2 = 1 \iff x^{-1} = x$，因为群中任意元素的逆唯一，可知 $x$ 与 $x^{-1}$ 必成对出现，所以不满足 $x^{-1} = x$ 的元素个数为偶数。又因为 $G$ 是偶数元群，所以 $G$ 中满足方程 $x^2 = 1$ 的解有偶数个。

阿贝尔群

若群 $(G, \cdot)$ 的运算 $\cdot$ 符合交换律，则称 $(G, \cdot)$ 为阿贝尔群（Abelian group）或交换群。在阿贝尔群 $(G, \cdot)$ 中，可以任意交换用 $\cdot$ 连接的因子的次序进行求值。

一元群、二元群和三元群都是唯一的，且都是阿贝尔群。

例：

• $(\Z, +), (\mathbb{Q}, +), (\R, +), (\mathbb{C}, +)$ 都是无限阿贝尔群。
• $(\mathbb{Q}^*, \cdot), (\R^*, \cdot), (\mathbb{C}^*, \cdot)$ 都是无限阿贝尔群。
• 实数域上所有 $n$ 阶非奇异矩阵的集合在矩阵的乘法下不是阿贝尔群。

定理： 设 $(G, \cdot)$ 是一个群，则 $(G, \cdot)$ 是阿贝尔群的充要条件是对任意 $a, b \in G$，有 $(a \cdot b)^2 = a^2 \cdot b^2$.

证明：

先证必要性：若 $(G, \cdot)$ 为阿贝尔群，即对任意 $a, b \in G$，都满足 $a \cdot b = b \cdot a$，所以

$$\begin{aligned} (a \cdot b)^2 &= (a \cdot b) \cdot (a \cdot b)\\ &= a \cdot (b \cdot a) \cdot b\\ &= a \cdot (a \cdot b) \cdot b\\ &= (a \cdot a) \cdot (b \cdot b)\\ &= a^2 \cdot b^2 \end{aligned}$$

再证充分性：对任意 $a, b \in G$，由 $(a \cdot b)^2 = a^2 \cdot b^2$，可得

$$a^{-1} \cdot (a \cdot b) \cdot (a \cdot b) \cdot b^{-1} = a^{-1} \cdot (a \cdot a) \cdot (b \cdot b) \cdot b^{-1}$$

所以 $b \cdot a = a \cdot b$，由此可得，$(G, \cdot)$ 为阿贝尔群。

定理： 阿贝尔群中的元素满足第三指数律 $(a \cdot b)^n = a^n \cdot b^n$（$n$ 为任意整数）。

永远假定加法群 $(G, +)$ 是阿贝尔群，加法群中的三个指数定律如下：

• $(m + n)a = ma + na$
• $m(na) = (mn)a$
• $n(a + b) = na + nb$

例：设 $(G, \cdot)$ 是一个群，若群 $G$ 的每一个元素都满足 $x^2 = 1$，证明 $G$ 是阿贝尔群。

证：对 $\forall x \in G$，由 $x^2 = 1$ 可得 $x^{-1} = x$，因此，对 $\forall a, b \in G$，有

$$a \cdot b = (a \cdot b)^{-1} = b^{-1} \cdot a^{-1} = b \cdot a$$

对称群与置换群

设 $S$ 是一个非空的有限集合，$S$ 到自身的一一映射（双射）称为置换（permutate），一般用 $\sigma$ 来表示。

设 $S = \{ a_1, a_2, \cdots, a_n \}$，则 $S$ 的置换 $\sigma$ 可以简记为

$$\sigma = \begin{pmatrix} a_1 & a_2 & \cdots & a_n \\ \sigma(a_1) & \sigma(a_2) & \cdots & \sigma(a_n) \end{pmatrix}$$

$S$ 上的置换称为 $n$ 元置换，共有 $n!$ 个，所有置换构成集合 $S_n$；若 $\sigma(a_i) = a_i,\ i = 1, 2, \cdots, n$，则称 $\sigma$ 为 $n$ 元恒等置换。

置换的乘法： 对 $S$ 中任意元素 $a$ 及 $S$ 的任意两个置换 $\sigma, \tau$，有

$$\sigma\tau(a) = \sigma(\tau(a))$$

置换的乘法满足结合律：

$$(\sigma\tau)\rho = \sigma(\tau\rho)$$

$n$ 元恒等置换是 $S_n$ 中的单位元素，记作 $\sigma_0$，满足

$$\sigma_0\tau = \tau\sigma_0$$

每个 $n$ 元置换在 $S_n$ 中都存在逆元素：

$$\sigma = \begin{pmatrix} a_1 & a_2 & \cdots & a_n \\ \sigma(a_1) & \sigma(a_2) & \cdots & \sigma(a_n) \end{pmatrix}^{-1} = \begin{pmatrix} \sigma(a_1) & \sigma(a_2) & \cdots & \sigma(a_n) \\ a_1 & a_2 & \cdots & a_n \end{pmatrix}$$

对称群（symmetric group）： 所有 $n$ 元置换构成的集合 $S_n$ 对置换的乘法构成一个群，称为 $\bm{n}$ 次对称群，它的任一子群称为 $\bm{n}$ 次置换群。

当 $n \leq 2$ 时，$n$ 次对称群为阿贝尔群，当 $n \geq 3$ 时则不是。

置换的轮换表示： 设 $\sigma$ 是 $S$ 的置换，若可以取到 $S$ 的元素 $a_1, a_2, \cdots, a_r$，使得

$$\sigma(a_1) = a_2,\ \sigma(a_2) = a_3,\ \cdots,\ \sigma(a_{r - 1}) = a_r,\ \sigma(a_r) = a_1$$

并且 $\sigma$ 不会改变 $S$ 的其余元素，则称 $\sigma$ 为 $S$ 的一个轮换，又称循环置换，记作 $(a_1\ a_2\ \cdots\ a_r)$.

在上述轮换中将 $a_1, a_2, \cdots, a_r$ 中的任意元素 $a_i$ 排在首位是等价的，因此也可以改写为 $(a_i\ a_{i + 1}\ \cdots\ a_r\ a_1\ \cdots\ a_{i - 1})$.

轮换的逆满足

$$(a_1\ a_2\ \cdots\ a_r)^{-1} = (a_r\ \cdots\ a_2\ a_1)$$

如果对于 $S$ 的两个轮换 $\sigma = (a_1\ a_2\ \cdots\ a_r)$ 和 $\tau = (b_1\ b_2\ \cdots\ b_r)$，满足 $a_1, a_2, \cdots, a_r$ 和 $b_1, b_2, \cdots, b_r$ 都不相同（即 $\{ a_1, a_2, \cdots, a_r \} \cap \{ b_1, b_2, \cdots, b_r \} = \empty$），则称这两个轮换不相交或不相杂。

若轮换 $\sigma$ 和 $\tau$ 不相交，则 $\sigma\tau = \tau\sigma$.

任意置换 $\sigma$ 恰有唯一方法写成不相交轮换的乘积（不考虑乘积的顺序），这种方法称为置换的轮换表示法。

例：

$$\begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\ 3 & 1 & 5 & 4 & 2 & 8 & 7 & 6 \end{pmatrix}\\ = (1\ 3\ 5\ 2)(4)(6\ 8)(7) = (3\ 5\ 2\ 1)(7)(8\ 6)(4)$$

对换： 长度（元素个数）为 2 的轮换称为对换，任意轮换可以写成对换的乘积，该写法不唯一：

$$(a_1\ a_2\ \cdots\ a_r) = (a_1\ a_r)(a_1\ a_{r - 1})\cdots(a_1\ a_3)(a_1\ a_2)$$

置换的奇偶性： 设 $n$ 元置换 $\sigma$ 可以表示为 $k$ 个不相交轮换的乘积，其长度分别为 $r_1, r_2, \cdots, r_k$，若

$$\sum_{j = 1}^k (r_j - 1) = n - k$$

为奇数 / 偶数，则称 $\sigma$ 为奇置换 / 偶置换。

由于每个长度为 $r$ 的轮换都可以写成 $r - 1$ 的对换的乘积，所以 $\sigma$ 可以写成 $\sum\limits_{j = 1}^k (r_j - 1) = n - k$ 个对换的乘积。

奇置换只能分解为奇数个对换的乘积，偶置换只能分解为偶数个对换的乘积。

定理： 设 $S$ 的元素个数为 $n\ (n > 1)$，则 $S_n$ 的所有 $n$ 元置换中，奇置换和偶置换的个数相同，且都为 $\dfrac{n!}{2}$.

交代群： $n$ 次对称群 $S_n$ 中的所有偶置换构成的有 $\dfrac{n!}{2}$ 个元素的群，记作 $A_n$。

例：计算 $(2\ 5\ 4)(1\ 2\ 4)(3\ 6\ 5)$，并将结果表示为不相交轮换的乘积形式，并指出其奇偶性。

解：

$$(2\ 5\ 4)(1\ 2\ 4)(3\ 6\ 5) = (1\ 5\ 3\ 6\ 4) = (1\ 5\ 3\ 6\ 4)(2)$$

因为 $n - k = 5 - 1 = 4$ 是偶数，所以该置换是偶置换。

子群的定义与判定

设 $(G, \cdot)$ 是一个群，如果存在 $H \subseteq G$，且 $(H, \cdot)$ 仍为群，则称 $(H, \cdot)$ 为 $(G, \cdot)$ 的子群（subgroup）。

如果子群 $H \subset G$，则称其为 $(G, \cdot)$ 的真子群。

任意群 $G$ 的两个平凡子群为：

• 由其单位元素构成的子群，称为 $G$ 的单位子群；
• $G$ 自身。

例：

• 对于任意整数 $k$，$(k\Z, +)$ 是整数加法群 $(\Z, +)$ 的一个子群。
• $(\mathbb{C}, +)$ 的真子群有 $(\R, +)$，$(\mathbb{Q}, +)$ 和 $(\Z, +)$.
• $(\mathbb{C}^{*}, \cdot)$ 的真子群有 $(\R^{*}, \cdot)$ 和 $(\mathbb{Q}^{*}, \cdot)$.
• 行列式等于 $1$ 的所有 $n$ 阶矩阵可以构成实数域上所有 $n$ 阶非奇异矩阵的乘法群的一个真子群。
• 对于任意 $n > 1$，$n$ 次交代群是 $n$ 次对称群的一个真子群。

子群的判定定理一： 群 $G$ 的一个非空子集 $H$ 是 $G$ 的子群的充要条件是：

1. 若 $a \in H, b \in H$ ，则 $a \cdot b \in H$；
2. 若 $a \in H$，则 $a^{-1} \in H$.

子群 $H$ 与群 $G$ 有以下关系：

• $H$ 的单位元就是 $G$ 的单位元；
• $H$ 中任意元素 $a$ 在 $H$ 中的逆元和 $a$ 在 $G$ 中的逆元相同。

子群的判定定理二： 群 $G$ 的一个非空子集 $H$ 是 $G$ 的子群的充要条件是：若 $a \in H, b \in H$，则 $a \cdot b^{-1} \in H$.

结论： 群 $G$ 的任意多个子群的交仍然是 $G$ 的子群。

子群的判定定理三： 群 $G$ 的一个有限非空子集 $H$ 是 $G$ 的子群的充要条件是 $H$ 对 $G$ 的运算是封闭的，即若 $a \in H, b \in H$，则 $ab \in H$.

如果 $(G, \cdot)$ 是有限群，则对 $G$ 的任意非空子集 $H$，只要运算 $\cdot$ 封闭，$(H, \cdot)$ 就是 $(G, \cdot)$ 的子群。

循环群与元素的阶

设 $a$ 是群 $G$ 的一个元素，$a$ 的所有幂构成的集合 $\{ a^n \mid n \in \Z \}$，可以形成 $G$ 的一个子群，称为由 $a$ 生成的循环子群，也可简称为循环群，记作 $\langle a \rangle$，并称 $a$ 为该循环子群的生成元。

证明：因为 $a^0 = e \in \langle a \rangle$，所以 $\langle a \rangle$ 为非空集合。任取 $\langle a \rangle$ 中两元素 $a^m, a^n$，有

$$a^m(a^n)^{-1} = a^{m}a^{-n} = a^{m - n} \in \langle a \rangle$$

由子群的判定定理二，可证得 $\langle a \rangle$ 为 $G$ 的子群。

若存在 $a \in G$，使得 $G = \langle a \rangle$，即 $G$ 中的每一个元素都可以表示为 $a$ 的幂，则称 $G$ 为一个循环群。

例：

• 整数加法群 $(\Z, +)$ 是由 $1$ 生成的循环群，$(n\Z, +)$ 是由 $n$ 生成的循环群。
• 设 $G$ 为 $4$ 次对称群，则由轮换 $(1\ 2)$ 生成的循环群为 $\{ I, (1\ 2) \}$.
• 设非零复数乘法群 $(\mathbb{C}^*, \cdot)$，则 $H_1 = \{ 1, -1, i, -i \}$ 是由 $i$ 生成的循环群，$H_2 = \{ 1, -1 \}$ 是由 $-1$ 生成的循环群，$H_3 = \{ \cdots, 2^{-2}, 2^{-1}, 2^0, 2, 2^2 \}$ 是由 $2$ 生成的循环群。

定理 1： 循环群的子群仍为循环群。

定理 2： 每个循环群都是阿贝尔群。

证明：设 $(G, \cdot)$ 为循环群，$g$ 为其生成元，则对任意 $a, b \in G$，有

$$a = g^r,\quad b = g^s\\ a \cdot b = g^r \cdot g^s = g^{r + s} = g^s \cdot g^r = b \cdot a$$

可证得 $G$ 为阿贝尔群。

元素的阶（周期）： 设 $a$ 是乘法群 $G$ 中的一个元素，使得 $a^n = e$ 成立的最小正整数 $n$ 称为 $a$ 的阶，记作 $|a|$；若不存在这样的 $n$，则称 $a$ 的阶为无穷大，记作 $|a| = \infty$.

• 单位元的阶为 $1$：$|e| = 1$；
• 任意元素和它的逆元具有相同的阶：$|a| = |a^{-1}|$；
• 若 $|a| = 2$，则 $a = a^{-1}$；
• 在 $n$ 元有限群中，每一元素的阶数有限，且最多为 $n$.

例：

• 在 $(\mathbb{C}^*, \cdot)$ 中，$1$ 的阶为 $1$，$-1$ 的阶为 $2$，$\pm i$ 的阶为 $4$，复数 $z = re^{i\theta}\ (i \neq 1)$ 的阶为无穷大。
• $4$ 次对称群中轮换 $(1\ 2\ 3\ 4)$ 的阶为 $4$：

$$\begin{aligned} (1\ 2\ 3\ 4)^2 &= (1\ 3)(2\ 4)\\ (1\ 2\ 3\ 4)^3 &= (1\ 4\ 3\ 2)\\ (1\ 2\ 3\ 4)^4 &= I \end{aligned}$$

• 实数域上所有 $2$ 阶非奇异矩阵的集合和矩阵乘法构成群 $(G, *)$，则 $G$ 中 $A = \begin{bmatrix} 0 & -1 \\ 1 & -1 \end{bmatrix}$ 的阶为 $3$：

$$\begin{aligned} A^2 &= \begin{bmatrix} -1 & 1 \\ 1 & -1 \end{bmatrix}\\ A^3 &= I \end{aligned}$$

结论 1： 若群 $G$ 中元素 $a$ 的阶为 $n$，则

1. $1, a, a^2, a^3, \cdots, a^{n - 1}$ 为 $n$ 个不同元素；
2. 当且仅当 $n | m$ 时，$a^m = e$；
3. 当且仅当 $n | (s - t)$ 时，$a^s = a^t$.

结论 2： 设 $a$ 为群 $G$ 的一个元素，则

• 若 $a$ 的阶为无穷大，则 $\langle a \rangle$ 为无限循环群，且由彼此不同的元素构成：

$$\cdots, a^{-2}, a^{-1}, 1, a, a^2, \cdots$$

• 若 $a$ 为 $n$ 阶，则 $\langle a \rangle$ 为 $n$ 元循环群，且由 $n$ 个彼此不同的元素构成：

$$1, a, a^2, a^3, \cdots, a^{n - 1}$$

在加法群中，$\langle a \rangle$ 应改为 $a$ 的所有倍数的集合：

$$\cdots, -2a, -a, 0, a, 2a, \cdots$$

使得 $na = 0$ 成立的最小正整数 $n$ 称为 $a$ 的阶。

循环群的生成元素：

• 无限循环群 $\langle a \rangle$ 中有两个生成元：$a, a^{-1}$；
• $n$ 元循环群 $\langle a \rangle$ 中，满足 $(n, k) = 1$ 的元素 $a^k$ 是生成元，总数可以用欧拉函数 $\varphi(n)$ 来计算。

陪集的定义与性质

为了引入陪集的概念，我们需要定义左同余和右同余：设 $H$ 是 $G$ 的子群，$a, b \in G$，若存在 $h \in H$，使得 $a = bh$，则称 $a$ 对模 $h$ 左同余于 $b$.

同理，可以定义右同余：若存在 $h \in H$，使得 $a = hb$，则称 $a$ 对模 $h$ 右同余于 $b$.

左 / 右同余都是等价关系。

群 $G$ 在关于群 $H$ 的左同余关系下的一个等价类称为 $H$ 的一个左陪集，即对于 $g \in G$，存在左陪集

$$gH = \{ gh \mid h \in H \}$$

同理，群 $G$ 在关于群 $H$ 的右同余关系下的一个等价类称为 $H$ 的一个右陪集，即对于 $g \in G$，存在右陪集

$$Hg = \{ hg \mid h \in H \}$$

例：设 $G$ 为整数加法群，$H$ 是整数 $m$ 的所有倍数构成的子群，因为加法构成阿贝尔群，所有 $H$ 的左右陪集相同。又由

$$a \equiv b \pmod h \quad (h \in H)$$

即

$$\begin{aligned} a &= b + h \quad (h \in H)\\ a &= b + km\\ a &\equiv b \pmod m \end{aligned}$$

可得，$H$ 的陪集就是模 $m$ 的剩余类。

求陪集的方法： 若 $G$ 是有限群，求其子群 $H$ 的左陪集：

1. $H$ 本身就是一个左陪集；
2. 任取 $a \in G, a \notin H$，求解 $aH$ 可得一个左陪集；
3. 任取 $b \in G, b \notin H \cup aH$，求解 $bH$ 又可得一个左陪集，如此类推；
4. 最终 $G$ 将被穷尽，且

$$G = H \cup aH \cup bH \cup \cdots$$

例：设 $a$ 的周期为 $15$，求子群 $H = \langle a^6 \rangle$ 在群 $G = \langle a \rangle$ 中的所有左陪集。

解：$a^{15} = e$

1. $H = \langle a^6 \rangle = \langle a^3 \rangle = \{ e, a^3, a^6, a^9, a^{12}\}$
2. $aH = a \langle a^6 \rangle = \{ a, a^4, a^7, a^{10}, a^{13}\}$
3. $a^2 H = a^2 \langle a^6 \rangle = \{ a^2, a^5, a^8, a^{11}, a^{14}\}$

定理： 设 $H$ 为群 $G$ 的有限子群，则 $H$ 的任意陪集的元数皆等于 $H$ 的元数。

证明：以左陪集为例，因为 $aH = \{ ah \mid h \in H \}$，又因为 $G$ 满足消去律，则由 $ax = ay$ 可以推出 $x = y$，所以 $H$ 中不同元素以 $a$ 左乘仍然会得到不同的元素，可得 $aH$ 的元数等于 $H$ 的元数。

陪集的性质：

1. $H$ 自身也是 $H$ 的陪集。
2. 当且仅当 $a \in H$ 时，$aH = H$.
3. $a$ 在陪集 $aH$ 中。
4. 对于陪集 $aH$ 中的任意元素 $b$，都有 $aH = bH$.
5. $aH = bH$ 的充要条件是 $a^{-1}b \in H$.
6. 任意两个陪集 $aH$ 和 $bH$ 要么相等，要么不相交。

正规子群与拉格朗日定理

正规子群： 若 $H$ 是群 $G$ 的子群，且对 $G$ 中任意元素 $g$，都满足 $gH = Hg$，则称 $H$ 为 $G$ 的正规子群。

结论：当且仅当对 $\forall g \in G$，满足 $gHg^{-1} \subseteq H$ 时，$H$ 为 $G$ 的正规子群。

定理： 设 $H$ 是群 $G$ 的正规子群，若 $A, B$ 是 $N$ 的陪集，则 $AB$ 也是 $H$ 的陪集。

证明：因为 $H$ 是正规子群，所以

$$Hb = bH$$

设 $A = aH$，$B = bH$，则

$$AB = aHbH = abHH = abH$$

所以 $AB$ 也是 $H$ 的陪集。

商群： 设 $H$ 是 $G$ 的正规子群，于是以陪集的运算为群的代数运算，$H$ 的所有陪集可以构成一个新的群 $\overline G$，称为商群，记作 $\overline{G} = \dfrac{G}{H}$。

拉格朗日定理： 设 $G$ 为有限群，则 $G$ 的任意子群的元数都可以整除 $G$ 的元数。

结论：

1. 设 $G$ 为有限群且元数为 $n$，则 $G$ 的任意子群的元数均为 $n$ 的因数；但对于 $n$ 的任意一个因数 $m$，未必存在 $G$ 的 $m$ 元子群。

2. 若 $G$ 为循环群且元数为 $n$，则对于 $n$ 的任意一个正因数 $m$，一定存在 $G$ 唯一的 $m$ 元子群。

3. 元数是质数的群，一定没有除了平凡子群以外的子群。

4. 设 $G$ 为有限群且元数为 $n$，则 $G$ 中任意元素的阶一定是 $n$ 的因数。

定理 1： 有限群 $G$ 的元数除以 $H$ 的元数所得的商称为 $\bm{H}$ 在 $\bm{G}$ 中的指数，记作 $[G : H]$，则 $H$ 的指数即为其左 / 右陪集的个数。

定理 2： 设 $G$ 为 $n$ 元有限群，则对任意 $a \in G$，都有 $a^n = 1$.

证明：因为 $G$ 为有限群，所以 $a$ 的阶必然有限，设为 $m$，则 $a$ 生成一个 $m$ 元循环群 $\langle a \rangle$. 由拉格朗日定理可得 $m | n$，因此 $a^n = 1$.

定理 3： 若群 $G$ 的元素个数为质数，则 $G$ 必为循环群。

证明：设 $G$ 的元数为质数 $p\ (p > 1)$，任取 $G$ 中非单位元 $a$，设 $a$ 的阶为 $m$，则 $\langle a \rangle$ 的元数为 $m\ (m > 1)$，由拉格朗日定理可得 $m | p$. 但因为 $p$ 为质数，必然有 $m = p$，所以 $G = \langle a \rangle$，即 $G$ 是由 $a$ 生成的循环群。

克莱因（Klein）四元群： 除了单位元以外，其它三个元素的阶均为 $2$，即每个元素的逆均为其自身。克莱因四元群是最小的非循环群，同时也是阿贝尔群。

$*$	e	a	b	c
e	e	a	b	c
a	a	e	c	b
b	b	c	e	a
c	c	b	a	e

$\{ I, (1\ 2)(3\ 4), (1\ 3)(2\ 4), (1\ 4)(2\ 3) \}$ 即为克莱因四元群。

同态映射与同构映射

同态映射： 设群 $(G, *)$ 和代数系统 $(K, \cdot)$，设 $\sigma$ 是 $G$ 到 $K$ 的映射，若对 $G$ 中任意元素 $a, b$，都有

$$\sigma(a * b) = \sigma(a) \cdot \sigma(b)$$

则称该映射 $\sigma$ 为同态映射。

若 $\sigma$ 同时也是满射，则可以称其为满同态映射。

例：设 $(G, *), (K, +)$ 是两个群，令映射

$$\sigma:\ x \to e, \quad x \in G$$

其中 $e$ 是 $K$ 的单位元。$\sigma$ 是 $G$ 到 $K$ 的映射，且对任意 $a, b \in G$，有

$$\sigma(a * b) = e = e + e = \sigma(a) + \sigma(b)$$

即 $\sigma$ 是 $G$ 到 $K$ 的同态映射，$\sigma(G) = \{ e \}$ 是 $K$ 的子群，记作 $G \sim \sigma(G)$.

这种同态映射关系在任意群中都存在。

定理： 设 $(G, *)$ 是一个群，$(K, \cdot)$ 是一个代数系统，$\sigma$ 是 $G$ 到 $K$ 中的一个同态映射，$G' = \sigma(G)$，则称 $G$ 与 $G'$ 同态（homomorphism），记作 $G \sim G'$，且满足：

1. $(G', \cdot)$ 是一个群；
2. $G'$ 的单位元 $e'$ 即为 $G$ 的单位元 $e$ 的像 $\sigma(e)$；
3. 对任意 $a \in G$，都有 $(\sigma(a))^{-1} = \sigma(a^{-1})$；
4. 若 $\sigma(a) = \sigma(b)$，则 $\sigma(a^{-1}) = \sigma(b^{-1})$.

例：对群 $(\Z, +)$ 和 $(\mathbb{C}^*, \cdot)$，令映射

$$\sigma : n \to i^n, \quad n \in \Z$$

其中 $i$ 是 $\mathbb{C}$ 的虚数单位。

则 $\sigma$ 是 $\Z$ 到 $\mathbb{C}^*$ 的一个映射，且对任意整数 $m, n$，有

$$\sigma(m + n) = i^{m + n} = i^m \cdot i^n = \sigma(m) \cdot \sigma(n)$$

可知 $\sigma$ 是 $\Z$ 到 $\mathbb{C}^*$ 的同态映射，且 $\Z \sim \sigma(\Z)$.

$\sigma(\Z) = \{ 1, -1, i, -i \}$ 是 $\mathbb{C}^*$ 的一个子群。

同构映射： 设群 $(G, *)$ 和代数系统 $(K, \cdot)$，若 $\sigma$ 是 $G$ 到 $K$ 的同态映射，且 $\sigma$ 同时是 $G$ 到 $\sigma(G)$ 的双射（一一映射），则称 $\sigma$ 为同构映射。

称 $G$ 与 $\sigma(G)$ 同构（isomorphism），记作 $G \cong \sigma(G)$.

结论： 无限循环群同构于整数加法群。

证明：设无限循环群 $G = \langle g \rangle$ 和整数加法群 $\Z$，则对 $\forall a \in G$，$\exists n \in \Z$，使得 $a = g^n$，令映射 $f : a \to n$.

（1）任取 $a = g^{n_1}, b = g^{n_2} \in G$，且 $a \neq b$，则 $n_1 \neq n_2$，而 $f(g^{n_1}) = n_1, f(g^{n_2} = n_2) = n_2$，所以 $f(a) \neq f(b)$，可得 $f$ 为单射。

（2）任取 $n \in \Z$，存在 $g^n$，满足 $f(g^n) = n$，所以 $f$ 是满射，又因为 $f$ 为双射，可得 $f$ 为满射。

（3）任取 $a, b \in G$，则存在 $i, j \in Z$，使得 $a = g^i, b =g^j$，则

$$f(g^{i} g^{j}) = f(g^{i + j}) = i + j = f(g^{i}) + f(g^{j})$$

综上所述，$f$ 是群 $G$ 到群 $Z$ 的同构映射，即 $G \cong \Z$.

结论： 整数加法群同构于偶数加法群。

证明：设整数加法群 $(\Z, +)$ 和偶数加法群 $(B, +)$，对 $\forall n \in \Z$，令映射 $f : n \to 2n$.

（1）$\forall m, n \in \Z$，若 $f(m) = f(n)$，即 $2m = 2n$，则 $m = n$，可得 $f$ 为单射。

（2）$\forall k \in B$，存在 $m \in \Z$，满足 $k = 2m$，所以 $f$ 是满射，又因为 $f$ 为双射，可得 $f$ 为满射。

（3）$\forall m, n \in \Z$，有

$$f(m + n) = 2(m + n) = 2m + 2n = f(m) + f(n)$$

综上所述，$f$ 是群 $\Z$ 到群 $B$ 的同构映射，即 $\Z \cong B$.

自同构映射： 设 $G$ 是一个群，若 $\sigma$ 是 $G$ 到自身的同构映射，则称 $\sigma$ 为自同构映射。

例：

• 恒等映射是最简单的自同构映射，称为恒等自同构映射。
• 设整数加法群 $(\Z, +)$，令 $\sigma : n \to -n\ (\forall n \in \Z)$，则 $\sigma$ 是群 $\Z$ 的一个自同构映射。
• 设 $G$ 是阿贝尔群，将 $G$ 的每个元素都映射为其逆元素的映射 $\sigma : a \to a^{-1}\ (\forall a \in G)$ 是 $G$ 的一个自同构映射。
• 设 $G$ 是群，则对 $\forall a \in G$，映射 $\sigma_a : x \to axa^{-1}\ (x \in G)$ 是 $G$ 的自同构映射，称为内自同构映射。

同态核： 设群 $G'$ 是群 $G$ 的同态群，且 $\sigma(G) = G'$，令 $N$ 为 $G$ 中所有映射到 $G'$ 中单位元 $e'$ 的元素 $g$ 的集合，即

$$N = \sigma^{-1}(e') = \{ g \mid g \in G, \sigma(g) = e' \}$$

则称 $N$ 为 $\sigma$ 的核。

例：设整数加法群 $G$ 和模 3 加法群 $G' = \{ 0, 1, 2 \}$，则映射 $x \to x \pmod 3\ (x \in G)$ 是 $G$ 到 $G'$ 的同态映射，且 $\sigma$ 的核为 $\{ g \mid g = 3a, a \in G \}$.

群的第一同态定理： 设群 $G'$ 是群 $G$ 的同态群，且 $\sigma(G) = G'$，于是 $\sigma$ 的核 $N$ 是 $G$ 的一个正规子群，对 $G'$ 中的任意元素 $a'$，有

$$\sigma^{-1}(a') = \{ x \mid x \in G, \sigma(x) = a' \}$$

并且 $\sigma^{-1}(a')$ 是 $N$ 在 $G$ 中的一个陪集。

群的第二同态定理： 设 $N$ 是群 $G$ 的正规子群，则映射

$$\sigma : a \to aN, \quad a \in G$$

是 $G$ 到 $\dfrac{G}{N}$ 的一个同态映射，且 $\sigma$ 的核即为 $N$.

群的第三同态定理： 设群 $G'$ 是群 $G$ 的同态群，且 $\sigma(G) = G'$，若 $\sigma$ 的核为 $N$，则 $G' \cong \dfrac{G}{N}$.

同态群的子群相关结论：

设群 $G'$ 是群 $G$ 的同态群，且 $\sigma(G) = G'$，则有以下结论成立：

结论 1： 若 $H$ 是群 $G$ 的子群，则 $H' = \sigma(H)$ 也是 $G'$ 的子群；若 $H'$ 是群 $G'$ 的子群，则 $H = \sigma^{-1}(H')$ 也是 $G$ 的子群，其中

$$\sigma^{-1}(H') = \{ x \mid x \in G, \sigma(x) \in H' \}$$

结论 2： $\sigma^{-1}(\sigma(H)) = HN$.

结论 3： 若 $N \subseteq H$，则 $HN = H$，即 $\sigma^{-1}(\sigma(H)) = H$.

结论 4： 若 $H$ 是 $G$ 的正规子群，则 $H' = \sigma(H)$ 也是 $G'$ 的正规子群；若 $H'$ 是 $G'$ 的正规子群，则 $H = \sigma^{-1}(H')$ 也是 $G$ 的正规子群。

环（Ring）与域（Field）

环的定义与性质

设 $R$ 是一个非空集合，其中有加法 “$+$” 和乘法 “$\cdot$” 两种二元代数运算，如果满足

1. $a + b = b + a$；
2. $a + (b + c) = (a + b) + c$；
3. $R$ 种存在元素 $0$，满足 $a + 0 = a$；
4. 对任意 $a \in R$，存在 $-a \in R$，使得 $a + (-a) = 0$；
5. $a \cdot (b \cdot c) = (a \cdot b) \cdot c$；
6. $a \cdot (b + c) = (a \cdot b) + (a \cdot c)$， $(a + b) \cdot c = (a \cdot c) + (b \cdot c)$.

则称 $(R, +, \cdot)$ 为一个环。

环的第一种证明方法：

1. $R$ 非空；
2. $+$ 具有封闭性，满足交换律和结合律；
3. $R$ 中存在加法单位元（通常称为环的零元）；
4. 对 $R$ 中任意元素，存在加法逆元；
5. $\cdot$ 具有封闭性，满足结合律；
6. $\cdot$ 对 $+$ 满足分配律；

环的第二种证明方法：

1. $(R, +)$ 是阿贝尔群；
2. $(R, \cdot)$ 是半群；
3. $\cdot$ 对 $+$ 满足分配律。

例：

• 所有整数在数的加法和乘法下构成一个环 $(\Z, +, \cdot)$，称为整数环。
• 所有 $n$ 阶矩阵在矩阵的加法和乘法下构成一个环，称为 $n$ 阶矩阵环。
• 整数模 $n$ 的所有剩余类集合，在剩余类的加法和乘法下可以构成一个群。
• 所有有理数、实数、复数，在数的加法和乘法下都可分别构成环，称为有理数域、实数域和复数域。

环的性质：

1. 分配律的推广：$\displaystyle\sum_{i = 1}^m a_i \sum_{j = 1}^n b_j = \sum_{i, j} a_i b_j$.

2. 减法的分配律：$a(c - b) = ac - ab, (c - b)a = ca - ba$.

3. 加法单位元即为乘法的零元：$a \cdot 0 = 0, \quad 0 \cdot a = 0$.

4. 乘数的符号可以交换和抵消：$a(-b) = -(ab), (-a)b = -(ab), (-a)(-b) = ab$.

5. 对任意整数 $m$，都有 $a(mb) = (ma)b = m(ab)$.

6. 指数定律：$a^{m + n} = a^m a^n, \quad (a^m)^n = a^{mn}$.

特殊环的定义与性质

交换环： 若环中的乘法也满足交换律，则称其是一个交换环。

交换环的性质：

1. 第三指数律成立：$(ab)^n = a^n b^n$.

2. 二项式定理成立：

$$(a + b)^n = a^n + na^{n - 1}b + \frac{n(n - 1)}{2}a^{n - 2}b^2 + \cdots + b^n$$

含单位元环： 若环 $R$ 中有且仅有一个元素 $e$ 满足对任意 $a \in R$，有 $ea = ae = a$，则 $e$ 为 $R$ 的单位元，称 $R$ 为含单位元环。

含单位元环的性质：

1. 含单位元环的单位元是唯一确定的。
2. 含单位元环的单位元 $e$ 和加法的单位元 $0$ 一定不相同。
3. 任意环 $R$ 均可扩充为一个含单位元环。

子环： 设 $R$ 是环，$S$ 是 $R$ 的非空子集，若 $S$ 在 $R$ 的加法和乘法运算下仍是环，则称 $S$ 是 $R$ 的子环。

$R$ 本身以及仅由零元构成的环 $\{ 0 \}$ 是 $R$ 的两个平凡子环。

若大环有单位元，其子环未必有单位元；即时子环有单位元，其单位元未必与大环的单位元一致。

定理： 环 $R$ 的非空子集 $S$ 构成子环的充要条件是对任意 $a \in S, b \in S$，满足 $a - b \in S, ab \in S$.

无零因子环： 设 $R$ 是环，$a, b \in R$，如果 $a \neq 0, b \neq 0$，但 $ab = 0$，则称 $a, b$ 为零因子。如果 $R$ 中不存在这样元素，则称其为无零因子环。

例：

• 整数环是无零因子环。
• 矩阵环不是无零因子环，例如当元素个数为 2 时，有

$$\begin{bmatrix} 0 & 1 \\ 0 & 0 \end{bmatrix} \begin{bmatrix} 1 & 0 \\ 0 & 0 \end{bmatrix} = \begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix}$$

无零因子环的性质：

1. 环 $R$ 是非零元环的充要条件是 $R$ 中的非零元在乘法运算中满足消去律。
2. 在无零因子环中，非零元在加法下的周期相同。
3. 在无零因子环中，非零元在加法下的周期为 0 或一个质数。

整区（integral domain）： 有单位元无零因子的交换环。

要证明环 $(R, +, \cdot)$ 是整区，需要证明：

1. $(R, +)$ 是阿贝尔群；
2. $(R, \cdot)$ 是有单位元的半群（单位半群）；
3. 群中元素满足交换律和消去律（无零因子）；
4. $\cdot$ 对 $+$ 满足分配律。

例：

• 整数环、有理数环、实数环复数环都是整区。
• 矩阵环既不是交换环也不是无零元环，因此不是整区。
• 整数模 4 的所有剩余类集合 $\Z_4$ 在剩余类的加法与乘法下构成一个含单位元的交换环，但其有零因子，所以不是整区。

除环（division ring）： 也称为体，是非零元素能构成一个乘法群的环。

要证明环 $(R, +, \cdot)$ 是除环，需要证明：

1. $(R, +)$ 是阿贝尔群；
2. 设 $R^*$ 是 $R$ 的非零元素构成的集合，则 $(R^*, \cdot)$ 是群；
3. $\cdot$ 对 $+$ 满足分配律。

结论：若 $R$ 是无零因子的有限环，且不只有一个元素，则 $R$ 必为除环。

域和子域

域： 交换除环即称为域。域中除法运算成立，即 $ab^{-1}$ 可以写成 $\dfrac{a}{b}$.

要证明环 $(R, +, \cdot)$ 是域，需要证明：

1. $(R, +)$ 是阿贝尔群；
2. $(R^*, \cdot)$ 是阿贝尔群；
3. $\cdot$ 对 $+$ 满足分配律。

在域中，每一个非零元素都具有两个与之相联系的周期，一个是在加法群中的加法周期，一个是在乘法群中的乘法周期。

例：在有理数域、实数域和复数域中，每个非零元素的加法周期都为 0（无穷大），1 的乘法周期为 1，-1 的乘法周期为 2，其它非零元的乘法周期为 0.

定理 1： 域中所有非零元素都有相同的加法周期，且为 0 或一个质数。

定理 2： 域是整区，有限整区是域。

子域： 若除环 $R$（域 $F$） 的一个子环仍为除环，则称为 $R$（$F$） 的子除环；若同时又为域，则称为 $R$（$F$） 的子域。

例：整数环是实数域的子环，实数域是复数域的子域。

格（Lattice）

偏序格与代数格

偏序格： 设偏序集 $(L, \leq)$, 如果对于任意 $a, b \in L$，$L$ 的子集 $\{a, b\}$ 在 $L$ 中都有一个最大下界 $\inf\{a, b\}$ 和一个最小上界 $\sup\{a, b\}$，则称 $(L，\leq)$ 为一个格。

结论：全序集必然是格，但偏序集不一定是格。

例 1：设 $\rho(S)$ 是任意集合 $S$ 的幂集，则对任意 $A, B \in \rho(S)$，有

$$\sup\{A, B\} = A \cup B \in \rho(S),\\ \inf\{A, B\} = A \cap B \in \rho(S)$$

因此部分序集 $(\rho(S), \subseteq)$ 是一个格。

例 2：设 $n$ 是正整数，$S_n$ 是 $n$ 的所有正因数的集合，$D$ 是整除关系，则对任意 $a, b \in S_n$，有

$$\sup\{a, b\} = a, b \ \text{的最小公倍数} \ \in \rho(S),\\ \inf\{a, b\} = a, b \ \text{的最大公因数} \ \in \rho(S)$$

因此 $(S_n, D)$ 是一个格。

格的 Hasse 图表示法：

需要注意的是，下列 Hasse 图不是格：

偏序子格： 设 $(L，\leq)$ 是格，$S \subseteq L$，如果 $(S，\leq)$ 也是格，则称 $(S，\leq)$ 是 $(L，\leq)$ 的一个子格。

代数格： 设 $L$ 是一个集合，$\wedge, \vee$ 是 $L$ 上的两个二元代数运算，如果这两种运算对 $L$ 中元素满足：

1. 交换律：$a \wedge b = b \wedge a, a \vee b = b \vee a$；
2. 结合律：$a \wedge (b \wedge c) = (a \wedge b) \wedge c, a \vee (b \vee c) = (a \vee b) \vee c$；
3. 吸收律：$a \wedge (a \vee b) = a, a \vee (a \wedge b) = a$.

则称该代数系统 $(L, \wedge, \vee)$ 为一个格。

由 $\wedge, \vee$ 满足吸收律可推出它们也满足幂等律。

定理： 若 $(L, \wedge, \vee)$ 是格，则 $(L, \wedge)$ 和 $(L, \vee)$ 是交换半群。

例 1：设 $\rho(S)$ 是任意集合 $S$ 的幂集，则 $(\rho(S), \cap, \cup)$ 是一个代数格。又因为 $(ρ(S)，\subseteq)$ 是偏序格，可见对任意 $A, B \in \rho(S)$，有

$$A \subseteq B \iff A \cap B = A \iff A \cup B = B$$

例 2：设 $n$ 是正整数，$S_n$ 是 $n$ 的所有正因数的集合，两个正整数的最大公因数运算为 $\wedge$，最小公倍数运算为 $\vee$，则 $(S_n, \wedge, \vee)$ 是一个代数格。又因为 $(S_n，D)$ 是偏序格，可见对任意 $a, b \in S_n$，有

$$aDb \iff a \wedge b = a \iff a \vee b = b$$

由上述例子，可以发现代数格与偏序格之间存在等价性，即：一个偏序格必是一个代数格；反之亦然。

代数子格： 设 $(L, \wedge, \vee)$ 是代数格，若对于 $S \subseteq L$，$S$ 在运算 $\wedge, \vee$ 下是封闭的，则称 $(S, \wedge, \vee)$ 是 $(L, \wedge, \vee)$ 的一个子格。

代数子格与偏序子格的关系： 设 $(L, \leq)$ 是偏序格，$(L, \wedge, \vee)$ 是与其等价的代数格，且 $S \subseteq L$，则

• 若 $(S, \wedge, \vee)$ 是 $(L, \wedge, \vee)$ 的代数子格，则 $(S, \leq)$ 是 $(L, \leq)$ 的偏序子格；
• 若 $(S, \leq)$ 是 $(L, \leq)$ 的偏序子格，则 $(S, \wedge, \vee)$ 不一定是 $(L, \wedge, \vee)$ 的代数子格。

例：设 $(L, \wedge, \vee)$ 是一个格，$a, b \in L$，令 $S = \{ x \mid (x \in L) \wedge (a \leq x \leq b) \}$，其中 $\leq$ 是与 $(L, \wedge, \vee)$ 等价的偏序格中的部分序关系，证明 $(S, \wedge, \vee)$ 是 $L$ 的子格。

证：设 $x, y \in S$，则 $x, y \in L$，且 $a \leq x, y \leq b$，所以

$$a \wedge a \leq x \wedge y \leq b \wedge b\\ a \vee a \leq x \vee y \leq b \vee b$$

即

$$a \leq x \wedge y \leq b, \quad a \leq x \vee y \leq b$$

因此 $x \wedge y, x \vee y \in L$，故运算 $\wedge, \vee$ 在 $S$ 上是封闭的，所以 $(S, \wedge, \vee)$ 是 $(L, \wedge, \vee)$ 的子格。

性质 1： 设 $(L, \leq)$ 是一个格，对于任意 $a, b \in L$，有

$$a \leq b \iff a \wedge b = a \iff a \vee b = b$$

性质 2： 设 $(L, \leq)$ 是一个格，对任意 $a, b, c \in L$，若 $b \leq c$，则有

$$a \wedge b \leq a \wedge c, \quad a \vee b \leq a \vee c$$

性质 3： 设 $(L, \leq)$ 是一个格，对任意 $a, b, c \in L$，有

$$a \vee (b \wedge c) \leq (a \vee b) \wedge (a \vee c)\\ (a \wedge b) \vee (a \wedge c) \leq a \wedge (b \vee c)$$

性质 4： 设 $(L, \leq)$ 是一个格，对任意 $a, b, c \in L$，有

$$a \leq b \iff a \vee (b \wedge c) \leq b \wedge (a \vee c)$$

例：设 $(L, \leq)$ 是格，证明：

1. $(a \wedge b) \vee (c \wedge d) \leq (a \vee c) \wedge (b \vee d)$；
2. $(a \wedge b) \vee (b \wedge c) \vee (c \wedge a) \leq (a \vee b) \wedge (b \vee c) \wedge (c \vee a)$.

证：

$$\begin{aligned} (a \wedge b) \vee (c \wedge d) &\leq [(a \wedge b) \vee c] \wedge [(a \wedge b) \vee d]\\ &\leq (a \vee c) \wedge (b \vee c) \wedge (a \vee d) \wedge (b \vee d)\\ &\leq [(a \vee c) \wedge (a \vee d)] \wedge [(b \vee d) \wedge (b \vee c)]\\ &\leq (a \vee c) \wedge (b \vee d) \end{aligned}$$

$$\begin{aligned} (a \wedge b) \vee (b \wedge c) \vee (c \wedge a) &\leq \{[(a \wedge b) \vee b] \wedge [(a \wedge b) \vee c]\} \vee (c \wedge a)\\ &= \{b \wedge [(a \wedge b) \vee c]\} \vee (c \wedge a)\\ &\leq \{[b \wedge [(a \wedge b) \vee c]] \vee c\} \wedge \{[b \wedge [(a \wedge b) \vee c]] \vee a\}\\ &\leq (b \vee c) \wedge \{[(a \wedge b) \vee c] \vee c\} \wedge (b \vee a) \wedge \{[(a \wedge b) \vee c] \vee a\}\\ &\leq (b \vee c) \wedge (a \vee b) \wedge (a \vee c) \wedge (b \vee c)\\ &= (a \vee b) \wedge (b \vee c) \wedge (c \vee a) \end{aligned}$$

$\bm{n}$ 维格： 规定

$$(a_1, \cdots, a_n) \leq_n (b_1, \cdots, b_n) \iff a_i \leq b_i \ (i = 1, \cdots, n)$$

由上述元素和运算构成的格称为 $n$ 维格，记作 $(L^n, \leq_n)$，与其等价的代数格记作 $(L^n, \wedge, \vee)$，于是对 $L^n$ 中任意两个元素，显然有

$$(a_1, \cdots, a_n) \wedge (b_1, \cdots, b_n) = (a_1 \wedge b_1, \cdots, a_n \wedge b_n)\\ (a_1, \cdots, a_n) \vee (b_1, \cdots, b_n) = (a_1 \vee b_1, \cdots, a_n \vee b_n)$$

格的同态与同构

设 $(L_1, \wedge, \vee)$ 和 $(L_2, \wedge', \vee')$ 是格，映射 $f : L_1 \to L_2$，若对任意 $a, b \in L_1$，满足

$$f(a \wedge b) = f(a) \wedge' f(b)\\ f(a \vee b) = f(a) \vee' f(b)$$

则称 $f$ 为格 $L_1$ 到 $L_2$ 的同态映射，简称格同态；格 $L$ 到自身的同态映射称为格的自同态映射。

若 $f : L_1 \to L_2$ 是双射（一一映射），则称格 $L_1$ 和格 $L_2$ 同构，此时对任意 $x \in L_1, y \in L_2$，有

$$f^{-1}(f(x)) = x, f(f^{-1}(y)) = y$$

同态保序定理： 设 $(L_1, \wedge, \vee) \equiv (L_1, \leq)$ 和 $(L_2, \wedge', \vee') \equiv (L_2, \leq')$ 是格，映射 $f : L_1 \to L_2$，

• 若 $f$ 是格同态映射，则 $f$ 具有保序性，即对任意 $a, b \in L_1$，$a \leq b \iff f(a) \leq' f(b)$；
• 若 $f$ 是双射，则 $f$ 为格同构映射当且仅当对任意 $a, b \in L_1$，$a \leq b \iff f(a) \leq' f(b)$.

定理 1： 设 $L$ 是格，$f$ 是其自同态映射，则 $f(x)$ 是 $L$ 的子格。

定理 2： 设 $L_1$ 和 $L_2$ 是格，若 $f : L_1 \to L_2$ 是同构映射，则 $f$ 的逆映射 $f^{-1}$ 是 $L_2$ 到 $L_1$ 的同构映射。

特殊格的定义与性质

有界格： 拥有一个最大元（记作全上界 1）和一个最小元（记作全下界 0）的格，即对任意 $a \in L$，都有 $0 \leq a \leq 1$.

结论：有限格必是有界格。令 $L = \{ a_1, a_2, \cdots, a_n \}$，则

$$0 = a_1 \wedge a_2 \wedge \cdots \wedge a_n\\ 1 = a_1 \vee a_2 \vee \cdots \vee a_n$$

但有界格不一定是有限格。

定理： 若 $(L, \wedge, \vee, 0, 1)$ 是有界格，则对任意 $a \in L$，恒有

$$a \vee 0 = a, \quad a \wedge 1 = a, \\ a \vee 1 = 1, \quad a \wedge 0 = 0$$

补元（余元）： 在有界格 $L$ 中，若存在 $a, b \in L$，满足 $a \wedge b = 0, a \vee b = 1$，则称 $b$ 为 $a$ 的补元。

在有界格中，一个元素可能没有补元，也可能有一个或一个以上的补元。1 是 0 唯一的补元，反之亦然。

例：

有补格（有余格，complemented lattice）： 若对有界格中任意一个元素，都至少有一个补元，则称该有界格为有补格。

例：设 $\rho(S)$ 是集合 $S$ 的幂集，于是 $(\rho(S)，\subseteq)$ 是有补格，并且 $\empty$ 和 $S$ 是此格的界。对任意元素 $A \in \rho(S)$，元素 $S - A \in \rho(S)$ 是其补元。

$n$ 维格 $(L^n, \leq_n)$ 是一个有补格，并且 $1_n = (1, 1, \cdots, 1), 0_n = (0, 0, \cdots, 0)$ 是界。对任意元素 $(a_1, \cdots, a_n) \in L^n$，存在元素 $(b_1, \cdots, b_n) \in L^n$ 是其补元，其中

$$b_i = 0 \iff a_i = 1, \quad b_i = 1 \iff a_i = 0, \quad (i = 1, \cdots, n)$$

分配格（distributive lattice）： 若代数格 $L$ 内的运算满足分配律，则称 $L$ 为分配格。即对任意 $a, b, c \in L$，有

$$a \wedge (b \vee c) = (a \wedge b) \vee (a \wedge c)\\ a \vee (b \wedge c) = (a \vee b) \wedge (a \vee c)$$

分配格的任意子格仍是分配格。

分配格定义中的两个等式是等价的：

$$\begin{aligned} (a \vee b) \wedge (a \vee c) &= ((a \vee b) \wedge a) \vee ((a \vee b) \wedge c)\\ &= a \vee ((a \wedge c) \vee (b \wedge c))\\ &= (a \vee (a \wedge c)) \vee (b \wedge c)\\ &= a \vee (b \wedge c) \end{aligned}$$

分配格与 Hasse 图的关系：

其中 $L_1$ 和 $L_2$ 是分配格，而 $L_3$ 和 $L_4$ 不是，在 $L_3$ 中

$$b \wedge (c \vee d) = b \wedge e = b\\ (b \wedge c) \vee (b \wedge d) = a \vee a = a$$

在 $L_4$ 中

$$d \wedge (b \vee c) = d \wedge e = d\\ (d \wedge b) \vee (d \wedge c) = a \vee c = c$$

形状类似 $L_3$ 的格称为钻石格，形状类似 $L_4$ 的格称为五角格。当且仅当 $L$ 不含有与钻石格或五角格同构的子格时，$L$ 是分配格。任意一个链都是分配格。

德摩根定律： 设 $(L, \wedge, \vee)$ 是分配格，对任意 $a, b \in L$，若存在对应的补元 $a', b'$，则

$$(a \wedge b)' = a' \vee b', \quad (a \vee b)' = a' \wedge b'$$

定理： 设 $(L, \wedge, \vee)$ 是分配格，对任意 $a, b, c \in L$，如果满足 $a \wedge c = b \wedge c, a \vee c = b \vee c$，则 $a = b$.

证明：

$$\begin{aligned} a &= a \wedge (a \vee c)\\ &= a \wedge (b \vee c)\\ &= (a \wedge b) \vee (a \wedge c)\\ &= (a \wedge b) \vee (b \wedge c)\\ &= b \wedge (a \vee c)\\ &= b \wedge (b \vee c)\\ &= b \end{aligned}$$

推论： 设 $(L, \wedge, \vee)$ 是有补分配格，则对任意 $a \in L$，$a$ 的补元 $a'$ 唯一。

证明：设 $a'$ 和 $a''$ 都是 $a$ 的补元，即

$$a \wedge a' = 0, \quad a \vee a' = 1\\ a \wedge a'' = 0, \quad a \vee a'' = 1$$

故 $a \wedge a' = a \wedge a'', a \vee a' = a \vee a''$，因此 $a' = a''$.

模格（modular lattice）： 若对格 $(L, \leq) \equiv (L, \wedge, \vee)$ 中的任意 $a, b, c \in L$，满足

$$a \leq b \iff a \vee (b \wedge c) = b \wedge (a \vee c)$$

则称 $L$ 为模格。

分配格都是模格，但模格不一定是分配格。

模格的充要条件： 对任意 $a, b, c \in L$，如果

$$a \leq b, \quad a \wedge c = b \wedge c, \quad a \vee c = b \vee c$$

则必有 $a = b$.

模格与 Hasse 图的关系：

其中 $L_1, L_2$ 和 $L_3$ 都是模格，而 $L_4$ 不是，在 $L_4$ 中

$$c \leq d, \quad c \vee (b \wedge d) = c, \quad (c \vee b) \wedge d = d$$

当且仅当 $L$ 不含有与五角格同构的子格时，$L$ 是模格，此时若 $L$ 不含有与钻石格同构的子格，则 $L$ 是分配格。