由于计算机中的数据都以离散量的形式存储,处于对研究数据结构和算法的需要,离散数学成为了计算机科学必备的前置科目。离散数学是一门证明较多,实用性较强的学科,因此概念和定理也非常繁杂。
离散量:逻辑量,图,树,整数,布尔代数等
命题逻辑
命题逻辑与联结词
所谓命题(proposition) ,是指一句有真假意义的话。我们用大写的英文字母 P , Q , R , ⋯ P,Q,R,\cdots P , Q , R , ⋯ 命题符号 。
如果一个命题为真,则称其真值为1,也用“1”代表一个抽象的真命题;如果一个命题为假,则称其真值为0,也用“0”代表一个抽象的假命题。
命题“P P P P P P 否定 ,记作 ¬ P \neg P ¬ P P P P ¬ P \neg P ¬ P ⟺ \iff ⟺ P P P
命题“P P P Q Q Q P , Q P,Q P , Q 析取(disjunctive) ,记作 P ∨ Q P\vee Q P ∨ Q P P P Q Q Q P ∨ Q P\vee Q P ∨ Q ⟺ \iff ⟺ P , Q P,Q P , Q
命题“P P P Q Q Q P , Q P,Q P , Q 合取(conjunction) ,记作 P ∧ Q P\wedge Q P ∧ Q P P P Q Q Q P ∧ Q P\wedge Q P ∧ Q ⟺ \iff ⟺ P , Q P,Q P , Q
自然语言中“或”有两种含义——表示两者可以同时成立,称为可兼或 ;表示二者只能居其一,不会同时成立,称为不可兼或 ,或异或(exclusive or) ,可以表示为:
( P ∧ ¬ Q ) ∨ ( ¬ P ∧ Q ) (P\wedge\neg Q)\vee(\neg P\wedge Q)
( P ∧ ¬ Q ) ∨ ( ¬ P ∧ Q )
命题“如果 P P P Q Q Q P P P 蕴涵 Q Q Q P P P implies Q Q Q P → Q P\rightarrow Q P → Q P → Q P\rightarrow Q P → Q ⟺ \iff ⟺ P P P Q Q Q
命题“P P P Q Q Q P P P 等价 Q Q Q P P P is equivalent to Q Q Q P ↔ Q P\leftrightarrow Q P ↔ Q P ↔ Q P\leftrightarrow Q P ↔ Q ⟺ \iff ⟺ P , Q P,Q P , Q
联结词的运算优先级(从高到低): ¬ , ∧ , ∨ , → , ↔ \neg,\wedge,\vee,\rightarrow,\leftrightarrow ¬ , ∧ , ∨ , → , ↔
命题公式
设 G G G A 1 , ⋯ , A n A_1,\cdots,A_n A 1 , ⋯ , A n G G G 原子(atom) ,指定 A 1 , ⋯ , A n A_1,\cdots,A_n A 1 , ⋯ , A n G G G 解释 I I I T I ( G ) T_{I}(G) T I ( G ) n n n 2 n 2^n 2 n
T I ( G ) = { m 1 , m 2 , ⋯ , m n } T_{I}(G)=\{m_1,m_2,\cdots,m_n\}
T I ( G ) = { m 1 , m 2 , ⋯ , m n }
m i = { A i 当 A i 在 I 下为 1 时 ¬ A i 当 A i 在 I 下为 0 时 i = 1 , 2 , ⋯ , n m_i=\begin{cases}A_i&\text{当}A_i\text{在}I\text{下为}1\text{时}\\\neg A_i&\text{当}A_i\text{在}I\text{下为}0\text{时}\end{cases}\\
i=1,2,\cdots,n m i = { A i ¬ A i 当 A i 在 I 下为 1 时 当 A i 在 I 下为 0 时 i = 1 , 2 , ⋯ , n
如果 G G G I I I I I I 满足 G G G G G G I I I I I I 弄假 G G G
公式 G G G G G G 真值表(truth table) 。
如果 G G G 恒真式(重言式) ;G G G 恒假式(矛盾式) ;G G G I I I G G G 可满足式 。
公式的等价:
如果 G , H G,H G , H I I I G , H G,H G , H 等价 的,记作 G = H G=H G = H G , H G,H G , H ⟺ \iff ⟺ G ↔ H G\leftrightarrow H G ↔ H
定律
基本等价式
单条件等价式
G ↔ H = ( G → H ) ∧ ( H → G ) G \leftrightarrow H=(G \rightarrow H)\wedge(H \rightarrow G) G ↔ H = ( G → H ) ∧ ( H → G )
双条件等价式
G → H = ¬ G ∨ H G \rightarrow H=\neg G \vee H G → H = ¬ G ∨ H
幂等律
G ∨ G = G G ∧ G = G G \vee G=G\\ G \wedge G=G G ∨ G = G G ∧ G = G
交换律
G ∨ H = H ∨ G G ∧ H = H ∧ G G \vee H=H \vee G\\ G \wedge H=H \wedge G G ∨ H = H ∨ G G ∧ H = H ∧ G
吸收律
G ∨ ( G ∧ H ) = G G ∧ ( G ∨ H ) = G G \vee(G \wedge H)=G\\ G \wedge(G \vee H)=G G ∨ ( G ∧ H ) = G G ∧ ( G ∨ H ) = G
分配律
G ∨ ( H ∧ S ) = ( G ∨ H ) ∧ ( G ∨ S ) G ∧ ( H ∨ S ) = ( G ∧ H ) ∨ ( G ∧ S ) G \vee(H \wedge S)=(G \vee H)\wedge(G \vee S)\\ G \wedge(H \vee S)=(G \wedge H)\vee(G \wedge S) G ∨ ( H ∧ S ) = ( G ∨ H ) ∧ ( G ∨ S ) G ∧ ( H ∨ S ) = ( G ∧ H ) ∨ ( G ∧ S )
同一律
G ∨ 0 = G G ∧ 1 = G G \vee 0=G\\ G \wedge 1=G G ∨ 0 = G G ∧ 1 = G
零一律
G ∨ 1 = 1 G ∧ 0 = 0 G \vee 1=1\\ G \wedge 0=0 G ∨ 1 = 1 G ∧ 0 = 0
互补律
G ∨ ¬ G = 1 G ∧ ¬ G = 0 G \vee \neg G=1\\ G \wedge \neg G=0 G ∨ ¬ G = 1 G ∧ ¬ G = 0
De Morgan 律
¬ ( G ∨ H ) = ¬ G ∧ ¬ H ¬ ( G ∧ H ) = ¬ G ∨ ¬ H \neg(G \vee H)=\neg G \wedge \neg H\\ \neg(G \wedge H)=\neg G \vee \neg H ¬ ( G ∨ H ) = ¬ G ∧ ¬ H ¬ ( G ∧ H ) = ¬ G ∨ ¬ H
利用基本等价式化简命题公式:
例:
( P → Q ) → P ∧ Q = ¬ ( ¬ P ∨ Q ) ∨ ( P ∧ Q ) = ( P ∧ ¬ Q ) ∨ ( P ∧ Q ) = P ∧ ( ¬ Q ∨ Q ) = P ∧ 1 = P \begin{aligned}
&\quad(P\rightarrow Q)\rightarrow P\wedge Q\\
&=\neg(\neg P\vee Q)\vee(P\wedge Q)\\
&=(P\wedge\neg Q)\vee(P\wedge Q)\\
&=P\wedge(\neg Q\vee Q)\\
&=P\wedge 1=P
\end{aligned} ( P → Q ) → P ∧ Q = ¬ ( ¬ P ∨ Q ) ∨ ( P ∧ Q ) = ( P ∧ ¬ Q ) ∨ ( P ∧ Q ) = P ∧ ( ¬ Q ∨ Q ) = P ∧ 1 = P
利用基本等价式判断命题公式是否恒真:
例:
( P → Q ) → ( ( Q → R ) → ( P → R ) ) = ¬ ( ¬ P ∨ Q ) ∨ ( ¬ ( ¬ Q ∨ R ) ∨ ( ¬ P ∨ R ) ) = ( P ∧ ¬ Q ) ∨ ( ( Q ∧ ¬ R ) ∨ ( ¬ P ∨ R ) ) = ( P ∧ ¬ Q ) ∨ ( ( Q ∨ ¬ P ∨ R ) ∧ ( ¬ R ∨ ¬ P ∨ R ) ) = ( P ∧ ¬ Q ) ∨ ( ( Q ∨ ¬ P ∨ R ) ∧ 1 ) = ( P ∧ ¬ Q ) ∨ ( Q ∨ ¬ P ∨ R ) = ( P ∨ Q ∨ ¬ P ∨ R ) ∧ ( ¬ Q ∨ Q ∨ ¬ P ∨ R ) = 1 ∨ 1 = 1 \begin{aligned}
&\quad(P\rightarrow Q)\rightarrow((Q\rightarrow R)\rightarrow(P\rightarrow R))\\
&=\neg(\neg P\vee Q)\vee(\neg(\neg Q\vee R)\vee(\neg P\vee R))\\
&=(P\wedge\neg Q)\vee((Q\wedge\neg R)\vee(\neg P\vee R))\\
&=(P\wedge\neg Q)\vee((Q\vee\neg P\vee R)\wedge(\neg R\vee\neg P\vee R))\\
&=(P\wedge\neg Q)\vee((Q\vee\neg P\vee R)\wedge 1)\\
&=(P\wedge\neg Q)\vee(Q\vee\neg P\vee R)\\
&=(P\vee Q\vee\neg P\vee R)\wedge(\neg Q\vee Q\vee\neg P\vee R)\\
&=1\vee 1=1
\end{aligned} ( P → Q ) → (( Q → R ) → ( P → R )) = ¬ ( ¬ P ∨ Q ) ∨ ( ¬ ( ¬ Q ∨ R ) ∨ ( ¬ P ∨ R )) = ( P ∧ ¬ Q ) ∨ (( Q ∧ ¬ R ) ∨ ( ¬ P ∨ R )) = ( P ∧ ¬ Q ) ∨ (( Q ∨ ¬ P ∨ R ) ∧ ( ¬ R ∨ ¬ P ∨ R )) = ( P ∧ ¬ Q ) ∨ (( Q ∨ ¬ P ∨ R ) ∧ 1 ) = ( P ∧ ¬ Q ) ∨ ( Q ∨ ¬ P ∨ R ) = ( P ∨ Q ∨ ¬ P ∨ R ) ∧ ( ¬ Q ∨ Q ∨ ¬ P ∨ R ) = 1 ∨ 1 = 1
所以原命题公式为恒真式。
联结词的完备集
设 Q Q Q Q Q Q Q Q Q Q Q Q 完备集 。
可以证明,{ ¬ , ∧ } \{\neg,\wedge\} { ¬ , ∧ } { ¬ , ∨ } \{\neg,\vee\} { ¬ , ∨ } { ¬ , → } \{\neg,\rightarrow\} { ¬ , → }
证明 { ¬ , ∧ } \{\neg,\wedge\} { ¬ , ∧ }
P ∨ Q = ¬ ( ¬ P ∧ ¬ Q ) P → Q = ¬ P ∨ Q = ¬ ( P ∧ ¬ Q ) P ↔ Q = ( P → Q ) ∧ ( Q → P ) = ( ¬ P ∨ Q ) ∧ ( ¬ Q ∨ P ) = ( ¬ ( P ∧ ¬ Q ) ) ∧ ( ¬ ( ¬ Q ∧ ¬ P ) ) \begin{aligned}
P\vee Q&=\neg(\neg P\wedge\neg Q)\\
P\rightarrow Q&=\neg P\vee Q=\neg(P\wedge\neg Q)\\
P\leftrightarrow Q&=(P\rightarrow Q)\wedge(Q\rightarrow P)\\
&=(\neg P\vee Q)\wedge(\neg Q\vee P)\\
&=(\neg(P\wedge\neg Q))\wedge(\neg(\neg Q\wedge\neg P))
\end{aligned} P ∨ Q P → Q P ↔ Q = ¬ ( ¬ P ∧ ¬ Q ) = ¬ P ∨ Q = ¬ ( P ∧ ¬ Q ) = ( P → Q ) ∧ ( Q → P ) = ( ¬ P ∨ Q ) ∧ ( ¬ Q ∨ P ) = ( ¬ ( P ∧ ¬ Q )) ∧ ( ¬ ( ¬ Q ∧ ¬ P ))
证明 { ¬ , ∨ } \{\neg,\vee\} { ¬ , ∨ }
P ∧ Q = ¬ ( ¬ P ∨ ¬ Q ) P → Q = ¬ P ∨ Q P ↔ Q = ( P → Q ) ∧ ( Q → P ) = ( ¬ P ∨ Q ) ∧ ( ¬ Q ∨ P ) = ¬ ( ¬ ( ¬ P ∨ Q ) ∨ ¬ ( ¬ Q ∨ P ) ) \begin{aligned}
P\wedge Q&=\neg(\neg P\vee\neg Q)\\
P\rightarrow Q&=\neg P\vee Q\\
P\leftrightarrow Q&=(P\rightarrow Q)\wedge(Q\rightarrow P)\\
&=(\neg P\vee Q)\wedge(\neg Q\vee P)\\
&=\neg(\neg(\neg P\vee Q)\vee\neg(\neg Q\vee P))
\end{aligned} P ∧ Q P → Q P ↔ Q = ¬ ( ¬ P ∨ ¬ Q ) = ¬ P ∨ Q = ( P → Q ) ∧ ( Q → P ) = ( ¬ P ∨ Q ) ∧ ( ¬ Q ∨ P ) = ¬ ( ¬ ( ¬ P ∨ Q ) ∨ ¬ ( ¬ Q ∨ P ))
证明 { ¬ , → } \{\neg,\rightarrow\} { ¬ , → }
P ∨ Q = ¬ P → Q P ∧ Q = ¬ ( ¬ P ∨ ¬ Q ) = ¬ ( P → ¬ Q ) P ↔ Q = ( P → Q ) ∧ ( Q → P ) = ¬ ( ( P → Q ) → ¬ ( Q → P ) ) \begin{aligned}
P\vee Q&=\neg P\rightarrow Q\\
P\wedge Q&=\neg(\neg P\vee\neg Q)\\
&=\neg(P\rightarrow\neg Q)\\
P\leftrightarrow Q&=(P\rightarrow Q)\wedge(Q\rightarrow P)\\
&=\neg((P\rightarrow Q)\rightarrow\neg(Q\rightarrow P))
\end{aligned} P ∨ Q P ∧ Q P ↔ Q = ¬ P → Q = ¬ ( ¬ P ∨ ¬ Q ) = ¬ ( P → ¬ Q ) = ( P → Q ) ∧ ( Q → P ) = ¬ (( P → Q ) → ¬ ( Q → P ))
与非式和或非式
命题“P P P Q Q Q P P P Q Q Q 与非式 ,记作 P ↑ Q P\uparrow Q P ↑ Q P ↑ Q P\uparrow Q P ↑ Q ⟺ \iff ⟺ P , Q P,Q P , Q
P ↑ Q = ¬ ( P ∧ Q ) P\uparrow Q=\neg(P\wedge Q)
P ↑ Q = ¬ ( P ∧ Q )
因为 { ¬ , ∧ } \{\neg,\wedge\} { ¬ , ∧ } { ↑ } \{\uparrow\} { ↑ }
命题“P P P Q Q Q P P P Q Q Q 或非式 ,记作 P ↓ Q P\downarrow Q P ↓ Q P ↓ Q P\downarrow Q P ↓ Q ⟺ \iff ⟺ P , Q P,Q P , Q
P ↓ Q = ¬ ( P ∨ Q ) P\downarrow Q=\neg(P\vee Q)
P ↓ Q = ¬ ( P ∨ Q )
因为 { ¬ , ∨ } \{\neg,\vee\} { ¬ , ∨ } { ↓ } \{\downarrow\} { ↓ }
公式的蕴涵与演绎推理
逻辑公式的一个重要作用就是研究命题推理,除了利用公式的等价关系进行推理以外,公式间的逻辑蕴涵(entailment)关系,也可以反映命题间的 演绎推理(deductive reasoning) :
设 G , H G,H G , H G , H G,H G , H I I I I I I G G G I I I H H H H H H G G G 逻辑结果 (G G G 蕴涵 H H H G ⇒ H G\Rightarrow H G ⇒ H
G ⇒ H G\Rightarrow H G ⇒ H ⟺ \iff ⟺ G → H G\rightarrow H G → H
证明:
必要性:任取 G , H G,H G , H I I I T I ( G ) = 1 T_I(G)=1 T I ( G ) = 1 G ⇒ H G\Rightarrow H G ⇒ H T I ( H ) = 1 T_I(H)=1 T I ( H ) = 1 T I ( G → H ) = 1 T_I(G\rightarrow H)=1 T I ( G → H ) = 1 T I ( G ) = 0 T_I(G)=0 T I ( G ) = 0 T I ( G → H ) = 1 T_I(G\rightarrow H)=1 T I ( G → H ) = 1 G , H G,H G , H I I I G → H G\rightarrow H G → H
充分性:任取 G , H G,H G , H I I I T I ( G ) = 1 T_I(G)=1 T I ( G ) = 1 G → H G\rightarrow H G → H T I ( H ) = 1 T_I(H)=1 T I ( H ) = 1 G ⇒ H G\Rightarrow H G ⇒ H
设 G 1 , G 2 , ⋯ , G n , H G_1,G_2,\cdots,G_n,H G 1 , G 2 , ⋯ , G n , H ( G 1 ∧ G 2 ∧ ⋯ ∧ G n ) ⇒ H (G_1\wedge G_2\wedge \cdots\wedge G_n)\Rightarrow H ( G 1 ∧ G 2 ∧ ⋯ ∧ G n ) ⇒ H H H H G 1 , G 2 , ⋯ , G n G_1,G_2,\cdots,G_n G 1 , G 2 , ⋯ , G n 逻辑结果 (G 1 , G 2 , ⋯ , G n G_1,G_2,\cdots,G_n G 1 , G 2 , ⋯ , G n 共同蕴涵 H H H
显然,( G 1 ∧ G 2 ∧ ⋯ ∧ G n ) ⇒ H (G_1\wedge G_2\wedge \cdots\wedge G_n)\Rightarrow H ( G 1 ∧ G 2 ∧ ⋯ ∧ G n ) ⇒ H ⟺ \iff ⟺ G 1 , G 2 , ⋯ , G n → H G_1,G_2,\cdots,G_n\rightarrow H G 1 , G 2 , ⋯ , G n → H
定理: 如果 H 1 , H 2 , ⋯ H m , P H_1,H_2,\cdots H_m,P H 1 , H 2 , ⋯ H m , P Q Q Q H 1 , H 2 , ⋯ H m H_1,H_2,\cdots H_m H 1 , H 2 , ⋯ H m P → Q P\rightarrow Q P → Q
演绎的定义:
设 S S S 前提集合 ,从 S S S G G G
G 1 , G 2 , ⋯ , G k G_1,G_2,\cdots,G_k
G 1 , G 2 , ⋯ , G k
其中,G k G_k G k G G G G i G_i G i S S S G j ( j < i ) G_j\ (j<i) G j ( j < i )
此时称从 S S S 演绎 出 G G G G G G S ⇒ G S\Rightarrow G S ⇒ G
演绎方法的完备性:
引理:设 G , H 1 , H 2 G,H_1,H_2 G , H 1 , H 2 G ⇒ H 1 , G ⇒ H 2 G\Rightarrow H_1,G\Rightarrow H_2 G ⇒ H 1 , G ⇒ H 2 G ⇒ ( H 1 ∧ H 2 ) G\Rightarrow(H_1\wedge H_2) G ⇒ ( H 1 ∧ H 2 )
证明:任取 G , H 1 , H 2 G,H_1,H_2 G , H 1 , H 2 I I I I I I G G G H 1 , H 2 H_1,H_2 H 1 , H 2 G G G I I I H 1 H_1 H 1 I I I H 2 H_2 H 2 I I I H 1 ∧ H 2 H_1\wedge H_2 H 1 ∧ H 2 I I I G ⇒ ( H 1 ∧ H 2 ) G\Rightarrow(H_1\wedge H_2) G ⇒ ( H 1 ∧ H 2 )
设 S S S G G G S S S G G G G G G S S S
证明:
必要性:设从 S S S G G G G 1 , G 2 , ⋯ , G k G_1,G_2,\cdots,G_k G 1 , G 2 , ⋯ , G k G i ( i = 1 , 2 , ⋯ , k ) G_i\ (i=1,2,\cdots,k) G i ( i = 1 , 2 , ⋯ , k ) G i G_i G i S S S
对 i i i
当 i = 1 i=1 i = 1 G 1 ∈ S G_1\in S G 1 ∈ S G 1 ∧ ⋯ → G 1 G_1\wedge\cdots\rightarrow G_1 G 1 ∧ ⋯ → G 1 S ⇒ G 1 S\Rightarrow G_1 S ⇒ G 1
当 i < n i<n i < n S ⇒ G i S\Rightarrow G_i S ⇒ G i
当 i = n i=n i = n G n ∈ S G_n\in S G n ∈ S S ⇒ G n S\Rightarrow G_n S ⇒ G n G n G_n G n G j ( j < n ) G_j\ (j<n) G j ( j < n ) ( G j 1 ∧ ⋯ ∧ G j h ) ⇒ G n (G_{j1}\wedge\cdots\wedge G_{jh})\Rightarrow G_n ( G j 1 ∧ ⋯ ∧ G jh ) ⇒ G n j 1 , ⋯ , j n < n j_1,\cdots,j_n<n j 1 , ⋯ , j n < n S ⇒ G j m , m = 1 , ⋯ , h S\Rightarrow G_{jm},\ m=1,\cdots,h S ⇒ G jm , m = 1 , ⋯ , h S ⇒ ( G j 1 ∧ ⋯ ∧ G j h ) S\Rightarrow(G_{j1}\wedge\cdots\wedge G_{jh}) S ⇒ ( G j 1 ∧ ⋯ ∧ G jh ) S ⇒ G n S\Rightarrow G_n S ⇒ G n
充分性:若 G G G S S S G G G H 1 , H 2 , ⋯ , H m , G H_1,H_2,\cdots,H_m,G H 1 , H 2 , ⋯ , H m , G H 1 , H 2 , ⋯ , H m H_1,H_2,\cdots,H_m H 1 , H 2 , ⋯ , H m S S S
演绎定理: 设 S S S G , H G,H G , H S ∪ { G } S\cup\{G\} S ∪ { G } H H H S S S G → H G\rightarrow H G → H
定律
基本蕴涵式
恒等律
0 ⇒ G G ⇒ 1 0\Rightarrow G\\ G\Rightarrow 1 0 ⇒ G G ⇒ 1
化简律
P ∧ Q ⇒ P P ∧ Q ⇒ Q P\wedge Q\Rightarrow P\\ P\wedge Q\Rightarrow Q P ∧ Q ⇒ P P ∧ Q ⇒ Q
附加律
P ⇒ P ∨ Q Q ⇒ P ∨ Q P\Rightarrow P\vee Q\\ Q\Rightarrow P\vee Q P ⇒ P ∨ Q Q ⇒ P ∨ Q
变形化简律
¬ ( P → Q ) ⇒ P ¬ ( P → Q ) ⇒ ¬ Q \neg(P\rightarrow Q)\Rightarrow P\\ \neg(P\rightarrow Q)\Rightarrow\neg Q ¬ ( P → Q ) ⇒ P ¬ ( P → Q ) ⇒ ¬ Q
变形附加律
¬ P ⇒ ( P → Q ) Q ⇒ ( P → Q ) \neg P\Rightarrow(P\rightarrow Q)\\ Q\Rightarrow(P\rightarrow Q) ¬ P ⇒ ( P → Q ) Q ⇒ ( P → Q )
前提引入规则
P , Q ⇒ P ∧ Q P,Q\Rightarrow P\wedge Q P , Q ⇒ P ∧ Q
析取三段论
¬ P , P ∨ Q ⇒ Q \neg P,P\vee Q\Rightarrow Q ¬ P , P ∨ Q ⇒ Q
假言推理
P , P → Q ⇔ Q P,P\rightarrow Q\Leftrightarrow Q P , P → Q ⇔ Q
拒取式
¬ Q , P → Q ⇔ ¬ P \neg Q,P\rightarrow Q\Leftrightarrow\neg P ¬ Q , P → Q ⇔ ¬ P
假言三段论
P → Q , Q → R ⇔ P → R P\rightarrow Q,Q\rightarrow R\Leftrightarrow P\rightarrow R P → Q , Q → R ⇔ P → R
二难推理
P ∨ Q , P → R , Q → R ⇔ R P\vee Q,P\rightarrow R,Q\rightarrow R\Leftrightarrow R P ∨ Q , P → R , Q → R ⇔ R
公式间蕴涵的证明方法:
给出两个公式 G , H G,H G , H G ⇒ H G\Rightarrow H G ⇒ H
真值表法,将公式 G G G H H H G G G H H H G ⇒ H G\Rightarrow H G ⇒ H
证 G → G\rightarrow G →
利用一些基本等价式和基本蕴涵式进行推导;
任取解释 I I I I I I G G G I I I H H H
反证法,设结论为假,只需证明前提也为假,即证明 ¬ H ⇒ ¬ G \neg H\Rightarrow\neg G ¬ H ⇒ ¬ G
自然演绎法推理
根据一些基本等价式和基本蕴涵式,可以从公式 S S S G G G
规则 P(前提引入规则,premise rule): 在推导的过程中,可随时引入前提集合中的任意一个前提。规则 T(逻辑结果引用规则,transformation rule): 在推导的过程中,可随时引入前面演绎出的某些公式的逻辑结果。规则 CP(附加前提规则,conclusion premise rule): 如果需要演绎出的公式是 P → Q P\rightarrow Q P → Q P P P Q Q Q
例:证明 { ( P ∨ Q ) , ( P → R ) , ( Q → S ) } ⇒ S ∨ R \{(P\vee Q),(P\rightarrow R),(Q\rightarrow S)\}\Rightarrow S\vee R {( P ∨ Q ) , ( P → R ) , ( Q → S )} ⇒ S ∨ R
证法一(不使用规则 CP):
( 1 ) P ∨ Q ( 2 ) ¬ P → Q ( 3 ) Q → S ( 4 ) ¬ P → S ( 5 ) ¬ S → P ( 6 ) P → R ( 7 ) ¬ S → R ( 8 ) S ∨ R \begin{align}
&(1)\quad P\vee Q\tag{P}\\
&(2)\quad \neg P\rightarrow Q\tag{T,1}\\
&(3)\quad Q\rightarrow S\tag{P}\\
&(4)\quad \neg P\rightarrow S\tag{T,2,3}\\
&(5)\quad \neg S\rightarrow P\tag{T,4}\\
&(6)\quad P\rightarrow R\tag{P}\\
&(7)\quad \neg S\rightarrow R\tag{T,5,6}\\
&(8)\quad S\vee R\tag{T,7}
\end{align} ( 1 ) P ∨ Q ( 2 ) ¬ P → Q ( 3 ) Q → S ( 4 ) ¬ P → S ( 5 ) ¬ S → P ( 6 ) P → R ( 7 ) ¬ S → R ( 8 ) S ∨ R ( P ) ( T,1 ) ( P ) ( T,2,3 ) ( T,4 ) ( P ) ( T,5,6 ) ( T,7 )
证法二(使用规则 CP):
( 1 ) ¬ S ( 2 ) Q → S ( 3 ) ¬ Q ( 4 ) P ∨ Q ( 5 ) P ( 6 ) P → R ( 7 ) R ( 8 ) ¬ S → R ( 9 ) S ∨ R \begin{align}
&(1)\quad \neg S\tag{CP}\\
&(2)\quad Q\rightarrow S\tag{P}\\
&(3)\quad \neg Q\tag{T,1,2}\\
&(4)\quad P\vee Q\tag{P}\\
&(5)\quad P\tag{T,3,4}\\
&(6)\quad P\rightarrow R\tag{P}\\
&(7)\quad R\tag{T,5,6}\\
&(8)\quad \neg S\rightarrow R\tag{CP,1,7}\\
&(9)\quad S\vee R\tag{T,8}
\end{align} ( 1 ) ¬ S ( 2 ) Q → S ( 3 ) ¬ Q ( 4 ) P ∨ Q ( 5 ) P ( 6 ) P → R ( 7 ) R ( 8 ) ¬ S → R ( 9 ) S ∨ R ( CP ) ( P ) ( T,1,2 ) ( P ) ( T,3,4 ) ( P ) ( T,5,6 ) ( CP,1,7 ) ( T,8 )
析取范式与合取范式
使用真值表来判定命题公式的真假虽然是万能的,但在公式包含原子数较多时,就会显得太过繁琐,为了简化两个命题公式是否等价及一个公式恒真、恒假、可满足的判定,我们引入范式(normal form) 的概念。
原子或原子的否定称为文字 ,有限个文字的析取式 称为一个子句 ,有限个文字的合取式 称为一个短语 。一个文字既可以称为是一个子句,也可以称为是一个短语。
有限个短语的析取式称为析取范式(disjunctive normal form,DNF) ;合取范式(conjunctive normal form,CNF) 。
定理: 对于任意命题公式,都存在与其等价的析取范式与合取范式。
对于公式 G G G G G G
使用基本等价式,将 G G G → , ↔ \rightarrow,\leftrightarrow → , ↔
使用 ¬ ( ¬ H ) = H \neg(\neg H)=H ¬ ( ¬ H ) = H G G G ¬ \neg ¬
反复使用分配律,即可得到等价于 G G G
极小项与主析取范式:
设 P 1 , P 2 , ⋯ , P n P_1,P_2,\cdots,P_n P 1 , P 2 , ⋯ , P n n n n 短语 如果恰好包含所有 这 n n n P 1 , P 2 , ⋯ , P n P_1,P_2,\cdots,P_n P 1 , P 2 , ⋯ , P n P 1 , P 2 , ⋯ , P n P_1,P_2,\cdots,P_n P 1 , P 2 , ⋯ , P n 极小项(minterm) ,对任意一个极小项 m m m 2 n 2^n 2 n
极小项与解释和 n n n
极小项
成真解释
记法
¬ P ∧ ¬ Q ∧ ¬ R \neg P\wedge\neg Q\wedge\neg R ¬ P ∧ ¬ Q ∧ ¬ R 000
m 0 m_0 m 0
¬ P ∧ ¬ Q ∧ R \neg P\wedge\neg Q\wedge R ¬ P ∧ ¬ Q ∧ R 001
m 1 m_1 m 1
¬ P ∧ Q ∧ ¬ R \neg P\wedge Q\wedge\neg R ¬ P ∧ Q ∧ ¬ R 010
m 2 m_2 m 2
¬ P ∧ Q ∧ R \neg P\wedge Q\wedge R ¬ P ∧ Q ∧ R 011
m 3 m_3 m 3
P ∧ ¬ Q ∧ ¬ R P\wedge\neg Q\wedge\neg R P ∧ ¬ Q ∧ ¬ R 100
m 4 m_4 m 4
P ∧ ¬ Q ∧ R P\wedge\neg Q\wedge R P ∧ ¬ Q ∧ R 101
m 5 m_5 m 5
P ∧ Q ∧ ¬ R P\wedge Q\wedge\neg R P ∧ Q ∧ ¬ R 110
m 6 m_6 m 6
P ∧ Q ∧ R P\wedge Q\wedge R P ∧ Q ∧ R 111
m 7 m_7 m 7
任意两个不同极小项的合取式恒假,所有极小项的析取式恒真:
⋁ i = 0 2 n − 1 m i = 1 \bigvee_{i=0}^{2^n-1}m_i=1
i = 0 ⋁ 2 n − 1 m i = 1
设命题公式 G G G P 1 , P 2 , ⋯ , P n P_1,P_2,\cdots,P_n P 1 , P 2 , ⋯ , P n G G G G ′ G' G ′ P 1 , P 2 , ⋯ , P n P_1,P_2,\cdots,P_n P 1 , P 2 , ⋯ , P n G ′ G' G ′ G G G 主析取范式(principal disjunctive normal form) 。在真值表中,使得公式为真的解释所对应的极小项的析取即为此公式的主析取范式。
定理: 对于任意命题公式,都存在唯一一个与其等价的主析取范式。
设命题公式 G G G P 1 , P 2 , ⋯ , P n P_1,P_2,\cdots,P_n P 1 , P 2 , ⋯ , P n
将公式 G G G G ′ G' G ′
删去析取范式中所有恒假的短语。
用等幂律将短语中重复出现的同一文字化简为只出现一次,例如 P ∧ P = P P\wedge P=P P ∧ P = P
对 G ′ G' G ′ G i ′ G_i' G i ′ P 1 , P 2 , ⋯ , P n P_1,P_2,\cdots,P_n P 1 , P 2 , ⋯ , P n G i ′ G_i' G i ′ P j 1 , ⋯ , P j k P_{j1},\cdots,P_{jk} P j 1 , ⋯ , P jk G i ′ G_i' G i ′ G G G
G i ′ = G i ′ ∧ ( P j 1 ∨ ¬ P j 1 ) ∧ ⋯ ∧ ( P j k ∨ ¬ P j k ) = m i 1 ∨ m i 2 ∨ ⋯ ∨ m i 2 k \begin{aligned}G_i'&=G_i'\wedge(P_{j1}\vee\neg P_{j1})\wedge\cdots\wedge(P_{jk}\vee\neg P_{jk})\\&=m_{i_1}\vee m_{i_2}\vee\cdots\vee m_{i_{2^k}}\end{aligned}
G i ′ = G i ′ ∧ ( P j 1 ∨ ¬ P j 1 ) ∧ ⋯ ∧ ( P jk ∨ ¬ P jk ) = m i 1 ∨ m i 2 ∨ ⋯ ∨ m i 2 k
极大项与主合取范式:
和极小项类似,设 P 1 , P 2 , ⋯ , P n P_1,P_2,\cdots,P_n P 1 , P 2 , ⋯ , P n n n n 子句 如果恰好包含所有 这 n n n P 1 , P 2 , ⋯ , P n P_1,P_2,\cdots,P_n P 1 , P 2 , ⋯ , P n P 1 , P 2 , ⋯ , P n P_1,P_2,\cdots,P_n P 1 , P 2 , ⋯ , P n 极大项(maxterm) ,对任意一个极大项 M M M
m i = ¬ M i , M i = ¬ m i m_i=\neg M_i,\quad M_i=\neg m_i
m i = ¬ M i , M i = ¬ m i
极大项
成假解释
记法
P ∨ Q ∨ R P\vee Q\vee R P ∨ Q ∨ R 000
M 0 M_0 M 0
P ∨ Q ∨ ¬ R P\vee Q\vee\neg R P ∨ Q ∨ ¬ R 001
M 1 M_1 M 1
P ∨ ¬ Q ∨ R P\vee\neg Q\vee R P ∨ ¬ Q ∨ R 010
M 2 M_2 M 2
P ∨ ¬ Q ∨ ¬ R P\vee\neg Q\vee\neg R P ∨ ¬ Q ∨ ¬ R 011
M 3 M_3 M 3
¬ P ∨ Q ∨ R \neg P\vee Q\vee R ¬ P ∨ Q ∨ R 100
M 4 M_4 M 4
¬ P ∨ Q ∨ ¬ R \neg P\vee Q\vee\neg R ¬ P ∨ Q ∨ ¬ R 101
M 5 M_5 M 5
¬ P ∨ ¬ Q ∨ R \neg P\vee\neg Q\vee R ¬ P ∨ ¬ Q ∨ R 110
M 6 M_6 M 6
¬ P ∨ ¬ Q ∨ ¬ R \neg P\vee\neg Q\vee\neg R ¬ P ∨ ¬ Q ∨ ¬ R 111
M 7 M_7 M 7
任意两个不同的极大项的析取式恒真,所有极大项的合取式恒假:
⋀ i = 0 2 n − 1 M i = 0 \bigwedge_{i=0}^{2^n-1}M_i=0
i = 0 ⋀ 2 n − 1 M i = 0
设命题公式 G G G P 1 , P 2 , ⋯ , P n P_1,P_2,\cdots,P_n P 1 , P 2 , ⋯ , P n G G G G ′ G' G ′ P 1 , P 2 , ⋯ , P n P_1,P_2,\cdots,P_n P 1 , P 2 , ⋯ , P n G ′ G' G ′ G G G 主合取范式(principal conjunctive normal form) 。在真值表中,使得公式为假的解释所对应的极大项的合取即为此公式的主合取范式。
定理: 对于任意命题公式,都存在唯一一个与其等价的主合取范式。
设命题公式 G G G P 1 , P 2 , ⋯ , P n P_1,P_2,\cdots,P_n P 1 , P 2 , ⋯ , P n
将公式 G G G G ′ G' G ′
删去合取范式中所有恒真的短语。
用等幂律将子句中重复出现的同一文字化简为只出现一次,例如 P ∨ P = P P\vee P=P P ∨ P = P
对 G ′ G' G ′ G i ′ G_i' G i ′ P 1 , P 2 , ⋯ , P n P_1,P_2,\cdots,P_n P 1 , P 2 , ⋯ , P n G i ′ G_i' G i ′ P j 1 , ⋯ , P j k P_{j1},\cdots,P_{jk} P j 1 , ⋯ , P jk G i ′ G_i' G i ′ G G G
G i ′ = G i ′ ∨ ( P j 1 ∧ ¬ P j 1 ) ∨ ⋯ ∨ ( P j k ∧ ¬ P j k ) = M i 1 ∧ M i 2 ∧ ⋯ ∧ M i 2 k \begin{aligned}G_i'&=G_i'\vee(P_{j1}\wedge\neg P_{j1})\vee\cdots\vee(P_{jk}\wedge\neg P_{jk})\\&=M_{i_1}\wedge M_{i_2}\wedge\cdots\wedge M_{i_{2^k}}\end{aligned}
G i ′ = G i ′ ∨ ( P j 1 ∧ ¬ P j 1 ) ∨ ⋯ ∨ ( P jk ∧ ¬ P jk ) = M i 1 ∧ M i 2 ∧ ⋯ ∧ M i 2 k
等价于同一公式的主析取范式 G ′ G' G ′ G ′ ′ G'' G ′′
G ′ ′ = ¬ ¬ G ′ = ¬ ¬ m 0 = ¬ ( m 1 ∨ m 2 ⋯ ∨ m k ) = ¬ m 1 ∧ ¬ m 2 ∧ ⋯ ∧ ¬ m k = M 1 ∧ M 2 ∧ ⋯ ∧ M k \begin{aligned}
G''&=\neg\neg G'\\
&=\neg\neg m_0\\
&=\neg(m_1\vee m_2\cdots\vee m_k)\\
&=\neg m_1\wedge\neg m_2\wedge\cdots\wedge\neg m_k\\
&=M_1\wedge M_2\wedge\cdots\wedge M_k
\end{aligned} G ′′ = ¬¬ G ′ = ¬¬ m 0 = ¬ ( m 1 ∨ m 2 ⋯ ∨ m k ) = ¬ m 1 ∧ ¬ m 2 ∧ ⋯ ∧ ¬ m k = M 1 ∧ M 2 ∧ ⋯ ∧ M k
通过如下方法即可将主析取范式转化为主合取范式:
求出 G G G m i m_i m i
求出与该极小项下标相同的极大项 M i M_i M i
将求出的所有极大项合取起来,即可得到 G G G G ′ G' G ′
用范式判断公式的等价性:
主析取范式和主合取范式都可以用来判断公式是否等价。因为等价于同一公式的主析取范式和主合取范式都是唯一的,所以假如对应于公式 G , H G,H G , H G , H G,H G , H
用范式判断公式的恒真恒假性:
析取范式法:公式 G G G G G G
主析取范式法:公式恒假时,主析取范式没有极小项(G ′ = 0 G'=0 G ′ = 0 G ′ = 1 G'=1 G ′ = 1
另一种判定算法:对任给要判定的命题公式 G G G P 1 , P 2 , ⋯ , P n P_1,P_2,\cdots,P_n P 1 , P 2 , ⋯ , P n 令 P 1 \bm{P_1} P 1 ,求 G G G G 1 G_1 G 1 P 2 , ⋯ , P n P_2,\cdots,P_n P 2 , ⋯ , P n 再令 P 1 \bm{P_1} P 1 ,求 G G G 只含0或1为止 。若最终结果全为1,则公式 G G G G G G G G G
例:求 ( P ∧ Q → R ) ∧ ( P → Q ) → ( P → R ) (P\wedge Q\rightarrow R)\wedge(P\rightarrow Q)\rightarrow(P\rightarrow R) ( P ∧ Q → R ) ∧ ( P → Q ) → ( P → R )
P P P ⇒ \Rightarrow ⇒ P P P ⇒ \Rightarrow ⇒ ( Q → R ) ∧ Q → R (Q\rightarrow R)\wedge Q\rightarrow R ( Q → R ) ∧ Q → R
Q Q Q ⇒ \Rightarrow ⇒ Q Q Q ⇒ \Rightarrow ⇒ R → R R\rightarrow R R → R
R R R ⇒ \Rightarrow ⇒ R R R ⇒ \Rightarrow ⇒
最终结果全为1,可得原公式恒真。
谓词逻辑
命题逻辑有一些严重的缺陷,那就是把问题看成一个个孤立的命题,忽略了问题之间的联系,不能反映某些重要的常见的逻辑思维过程。为解决这些问题,我们引入了谓词和谓词逻辑的概念。
谓词逻辑与量词
我们首先提出个体的定义:可以独立存在 的物体称为个体(individual) ,在谓词演算中,个体通常指一个命题里的思维对象;个体变化的范围称为个体域(individual domain) ,个体域可以是有限的,也可以是无限的;具象的个体称为个体常元(individual constant) ,抽象的个体称为个体变元(individual variable) ,变元可以被个体域内的任意一个元素代入。
用用于描述个体的性质或个体之间关系的词就称为谓词(predicate) ,含有 n n n n \bm n n 元谓词 ,记作 P ( x 1 , x 2 , ⋯ , x n ) P(x_1,x_2,\cdots,x_n) P ( x 1 , x 2 , ⋯ , x n )
命题“对任意 x x x G ( x ) G(x) G ( x ) 全称命题 ,记作 ∀ x G ( x ) \forall xG(x) ∀ x G ( x ) ∀ x \forall x ∀ x 全称量词(universal quantifier) 。∀ x G ( x ) \forall xG(x) ∀ x G ( x ) ⟺ \iff ⟺ x x x G ( x ) G(x) G ( x ) ∀ x G ( x ) \forall xG(x) ∀ x G ( x ) ⟺ \iff ⟺ x 0 x_0 x 0 G ( x 0 ) G(x_0) G ( x 0 )
命题“存在 x x x G ( x ) G(x) G ( x ) 存在命题 ,记作 ∃ x G ( x ) \exists xG(x) ∃ x G ( x ) ∃ x \exists x ∃ x 存在量词(existential quantifier) 。∃ x G ( x ) \exists xG(x) ∃ x G ( x ) ⟺ \iff ⟺ x 0 x_0 x 0 G ( x 0 ) G(x_0) G ( x 0 ) ∃ x G ( x ) \exists xG(x) ∃ x G ( x ) ⟺ \iff ⟺ x x x G ( x ) G(x) G ( x )
∀ x G ( x ) ⇒ G ( a ) ⇒ ∃ x G ( x ) ¬ ∃ x G ( x ) ⇒ ¬ ∀ x G ( x ) \forall xG(x)\Rightarrow G(a)\Rightarrow\exists xG(x)\\
\ \\
\neg\exists xG(x)\Rightarrow\neg \forall xG(x) ∀ x G ( x ) ⇒ G ( a ) ⇒ ∃ x G ( x ) ¬∃ x G ( x ) ⇒ ¬∀ x G ( x )
量词本身不是一个独立的逻辑概念,可以用析取和合取代替。当个体域 D = { x 0 , x 1 , ⋯ } D=\{x_0,x_1,\cdots\} D = { x 0 , x 1 , ⋯ }
∀ x G ( x ) ⟺ G ( x 0 ) ∧ G ( x 1 ) ∧ ⋯ ∃ x G ( x ) ⟺ G ( x 0 ) ∨ G ( x 1 ) ∨ ⋯ \forall xG(x)\iff G(x_0)\wedge G(x_1)\wedge\cdots\\
\ \\
\exists xG(x)\iff G(x_0)\vee G(x_1)\vee\cdots ∀ x G ( x ) ⟺ G ( x 0 ) ∧ G ( x 1 ) ∧ ⋯ ∃ x G ( x ) ⟺ G ( x 0 ) ∨ G ( x 1 ) ∨ ⋯
量词的约束范围:
当变元至少一次出现在使用这个变元的量词范围之内,则该变元受量词约束,称其为约束变元(bound variable) ;当变元至少一次出现在使用这个变元的量词范围之外,则该变元不受量词约束,称其为自由变元(free variable) 。一个变元可以既是约束变元又是自由变元。
约束变元的名称可以被更改,但这种改名必须在量词作用区域内各处 以及该量词符号中 同时进行,并且改成的新约束变元必须有别于 改名区域中的所有其它变元。
谓词公式
为了给出谓词公式的定义,我们需要先引入项(term) 的概念。谓词逻辑中的项具有如下递归定义:
个体常元是项;
个体变元是项;
若 f ( x 1 , x 2 , ⋯ , x n ) f(x_1,x_2,\cdots,x_n) f ( x 1 , x 2 , ⋯ , x n ) n n n x 1 , x 2 , ⋯ , x n x_1,x_2,\cdots,x_n x 1 , x 2 , ⋯ , x n f ( x 1 , x 2 , ⋯ , x n ) f(x_1,x_2,\cdots,x_n) f ( x 1 , x 2 , ⋯ , x n )
有限次使用以上规则生成的符号串都是项。
若 P ( x 1 , ⋯ , x n ) P(x_1,\cdots,x_n) P ( x 1 , ⋯ , x n ) n n n t 1 , ⋯ , t n t_1,\cdots,t_n t 1 , ⋯ , t n P ( x 1 , ⋯ , x n ) P(x_1,\cdots,x_n) P ( x 1 , ⋯ , x n ) 原子 。
谓词公式具有如下递归定义:
原子是公式;
若 G , H G,H G , H ( ¬ G ) (\neg G) ( ¬ G ) ( G ∨ H ) (G\vee H) ( G ∨ H ) ( G ∧ H ) (G\wedge H) ( G ∧ H ) ( G → ) (G\rightarrow) ( G → ) ( G ↔ G ) (G\leftrightarrow G) ( G ↔ G )
若 G G G x x x G G G ∀ x G \forall xG ∀ x G ∃ x G \exists xG ∃ x G
有限次使用以上规则生成的符号串都是公式。
若公式中无自由变元,或将自由变元看作常元,则称其为封闭公式 ,只有封闭公式可以看作命题,并且有确定的真值。
谓词公式 G G G 解释 I \bm I I D D D G G G
对每个个体常元,指定 D D D
对每个 n n n
对每个 n n n
例:证明 ∀ x ∃ y P ( x , y ) \forall x\exists yP(x,y) ∀ x ∃ y P ( x , y ) ∃ y ∀ x P ( x , y ) \exists y\forall xP(x,y) ∃ y ∀ x P ( x , y )
证:对函数 P ( x , y ) P(x,y) P ( x , y )
P ( 1 , 1 ) = 1 , P ( 1 , 2 ) = 0 , P ( 2 , 1 ) = 0 , P ( 2 , 2 ) = 1 P(1,1)=1,P(1,2)=0,P(2,1)=0,P(2,2)=1
P ( 1 , 1 ) = 1 , P ( 1 , 2 ) = 0 , P ( 2 , 1 ) = 0 , P ( 2 , 2 ) = 1
考虑论域 D = { 1 , 2 } D=\{1,2\} D = { 1 , 2 } I I I
T I ( ∀ x ∃ y P ( x , y ) ) = T I ( P ( 1 , 1 ) ∨ P ( 1 , 2 ) ) ∧ ( P ( 2 , 1 ) ∨ P ( 2 , 2 ) ) = 1 T I ( ∃ y ∀ x P ( x , y ) ) = T I ( P ( 1 , 1 ) ∧ P ( 1 , 2 ) ) ∨ ( P ( 2 , 1 ) ∧ P ( 2 , 2 ) ) = 0 T_I(\forall x\exists yP(x,y))=T_I(P(1,1)\vee P(1,2))\wedge(P(2,1)\vee P(2,2))=1\\
T_I(\exists y\forall xP(x,y))=T_I(P(1,1)\wedge P(1,2))\vee(P(2,1)\wedge P(2,2))=0 T I ( ∀ x ∃ y P ( x , y )) = T I ( P ( 1 , 1 ) ∨ P ( 1 , 2 )) ∧ ( P ( 2 , 1 ) ∨ P ( 2 , 2 )) = 1 T I ( ∃ y ∀ x P ( x , y )) = T I ( P ( 1 , 1 ) ∧ P ( 1 , 2 )) ∨ ( P ( 2 , 1 ) ∧ P ( 2 , 2 )) = 0
所以二者不等价。
在使用量词时,要注意多重量词的运算顺序和量词的作用范围。
不同的量词运算顺序:
构造解释 I I I D D D P ( x , y ) : x > y P(x,y):x>y P ( x , y ) : x > y
(1)
T I ( ∀ x ∃ y P ( x , y ) ) = T I ( ∃ y P ( 0 , y ) ∧ ∃ y P ( 1 , y ) ∧ ⋯ ∧ ∃ y ( P , n , y ) ∧ ⋯ ) T_I(\forall x\exists yP(x,y))=T_I(\exists yP(0,y)\wedge\exists yP(1,y)\wedge\cdots\wedge\exists y(P,n,y)\wedge\cdots)
T I ( ∀ x ∃ y P ( x , y )) = T I ( ∃ y P ( 0 , y ) ∧ ∃ y P ( 1 , y ) ∧ ⋯ ∧ ∃ y ( P , n , y ) ∧ ⋯ )
因为
T I ( ∃ y P ( 0 , y ) ) = T I ( P ( 0 , 0 ) ∨ P ( 0 , 1 ) ∨ ⋯ ) = 0 T_I(\exists yP(0,y))=T_I(P(0,0)\vee P(0,1)\vee\cdots)=0
T I ( ∃ y P ( 0 , y )) = T I ( P ( 0 , 0 ) ∨ P ( 0 , 1 ) ∨ ⋯ ) = 0
所以 T I ( ∀ x ∃ y P ( x , y ) ) = 0 T_I(\forall x\exists yP(x,y))=0 T I ( ∀ x ∃ y P ( x , y )) = 0
(2)
T I ( ∀ y ∃ x P ( x , y ) ) = T I ( ∃ x P ( x , 0 ) ∧ ∃ x P ( x , 1 ) ∧ ⋯ ∧ ∃ x P ( x , n ) ∧ ⋯ ) = 1 ∧ 1 ∧ ⋯ ∧ 1 ∧ ⋯ = 1 \begin{aligned}T_I(\forall y\exists xP(x,y))&=T_I(\exists xP(x,0)\wedge\exists xP(x,1)\wedge\cdots\wedge\exists xP(x,n)\wedge\cdots)\\&=1\wedge 1\wedge\cdots\wedge 1\wedge\cdots\\&=1\end{aligned}
T I ( ∀ y ∃ x P ( x , y )) = T I ( ∃ x P ( x , 0 ) ∧ ∃ x P ( x , 1 ) ∧ ⋯ ∧ ∃ x P ( x , n ) ∧ ⋯ ) = 1 ∧ 1 ∧ ⋯ ∧ 1 ∧ ⋯ = 1
(3)
T I ( ∃ x ∀ y P ( x , y ) ) = T I ( ∀ y P ( 0 , y ) ∨ ∀ y P ( 1 , y ) ∨ ⋯ ∨ ∀ y P ( n , y ) ∨ ⋯ ) = 0 ∨ 0 ∨ ⋯ ∨ 0 ∨ ⋯ = 0 \begin{aligned}T_I(\exists x\forall yP(x,y))&=T_I(\forall yP(0,y)\vee\forall yP(1,y)\vee\cdots\vee\forall yP(n,y)\vee\cdots)\\&=0\vee 0\vee\cdots\vee 0\vee\cdots\\&=0\end{aligned}
T I ( ∃ x ∀ y P ( x , y )) = T I ( ∀ y P ( 0 , y ) ∨ ∀ y P ( 1 , y ) ∨ ⋯ ∨ ∀ y P ( n , y ) ∨ ⋯ ) = 0 ∨ 0 ∨ ⋯ ∨ 0 ∨ ⋯ = 0
综上所述,∀ x ∃ y P ( x , y ) \forall x\exists yP(x,y) ∀ x ∃ y P ( x , y ) ∀ y ∃ x P ( x , y ) \forall y\exists xP(x,y) ∀ y ∃ x P ( x , y ) ∃ x ∀ y P ( x , y ) \exists x\forall yP(x,y) ∃ x ∀ y P ( x , y )
当论域 D D D
∀ x ∀ y P ( x , y ) = ∀ y ∀ x P ( x , y ) ∃ x ∃ y P ( x , y ) = ∃ y ∃ x P ( x , y ) \forall x\forall yP(x,y)=\forall y\forall xP(x,y)\\
\exists x\exists yP(x,y)=\exists y\exists xP(x,y) ∀ x ∀ y P ( x , y ) = ∀ y ∀ x P ( x , y ) ∃ x ∃ y P ( x , y ) = ∃ y ∃ x P ( x , y )
不同的量词作用范围:
∀ x P ( x ) → P ( a ) \forall xP(x)\rightarrow P(a) ∀ x P ( x ) → P ( a ) ∀ x ( P ( x ) → P ( a ) ) \forall x(P(x)\rightarrow P(a)) ∀ x ( P ( x ) → P ( a ))
设 D D D a ∈ D a\in D a ∈ D P ( x ) P(x) P ( x ) D D D
(1)任取解释 I I I P ( a ) P(a) P ( a ) I I I ∀ x P ( x ) → P ( a ) \forall xP(x)\rightarrow P(a) ∀ x P ( x ) → P ( a ) I I I P ( a ) P(a) P ( a ) I I I ∀ x P ( x ) \forall xP(x) ∀ x P ( x ) I I I ∀ x P ( x ) → P ( a ) \forall xP(x)\rightarrow P(a) ∀ x P ( x ) → P ( a ) I I I ∀ x P ( x ) → P ( a ) \forall xP(x)\rightarrow P(a) ∀ x P ( x ) → P ( a )
(2)构造解释 I I I D = { 1 , 2 } D=\{1,2\} D = { 1 , 2 } a = 1 a=1 a = 1 P ( 1 ) = 0 , P ( 2 ) = 0 P(1)=0,P(2)=0 P ( 1 ) = 0 , P ( 2 ) = 0
T I ( ∀ x ( P ( x ) → P ( a ) ) ) = T I ( ( P ( 1 ) → P ( 1 ) ) ∧ ( P ( 2 ) → P ( 1 ) ) ) = 1 ∧ 0 = 0 \begin{aligned}T_I(\forall x(P(x)\rightarrow P(a)))&=T_I((P(1)\rightarrow P(1))\wedge(P(2)\rightarrow P(1)))\\&=1\wedge 0 \\&=0\end{aligned}
T I ( ∀ x ( P ( x ) → P ( a ))) = T I (( P ( 1 ) → P ( 1 )) ∧ ( P ( 2 ) → P ( 1 ))) = 1 ∧ 0 = 0
因此,∀ x ( P ( x ) → P ( a ) ) \forall x(P(x)\rightarrow P(a)) ∀ x ( P ( x ) → P ( a ))
综上所述,∀ x P ( x ) → P ( a ) \forall xP(x)\rightarrow P(a) ∀ x P ( x ) → P ( a ) ∀ x ( P ( x ) → P ( a ) ) \forall x(P(x)\rightarrow P(a)) ∀ x ( P ( x ) → P ( a ))
谓词公式的等价与蕴涵
谓词公式的等价与蕴涵和命题公式类似。因为对任意谓词公式 G , H G,H G , H I I I G , H G,H G , H 基本等价式 在谓词逻辑中仍然成立;同理,命题逻辑中给出的基本蕴涵式 在谓词逻辑中也仍然成立。
此外,谓词逻辑还引入了一些新的常用基本等价式与蕴涵式:
定律
基本等价式
量词辖域扩张及收缩律 \\ H H H x x x
∀ x ( G ( x ) ∨ H ) = ∀ x G ( x ) ∨ H ∃ x ( G ( x ) ∨ H ) = ∃ x G ( x ) ∨ H ∀ x ( G ( x ) ∧ H ) = ∀ x G ( x ) ∧ H ∃ x ( G ( x ) ∧ H ) = ∃ x G ( x ) ∧ H \forall x(G(x)\vee H)=\forall xG(x)\vee H\\ \exists x(G(x)\vee H)=\exists xG(x)\vee H\\ \forall x(G(x)\wedge H)=\forall xG(x)\wedge H\\ \exists x(G(x)\wedge H)=\exists xG(x)\wedge H ∀ x ( G ( x ) ∨ H ) = ∀ x G ( x ) ∨ H ∃ x ( G ( x ) ∨ H ) = ∃ x G ( x ) ∨ H ∀ x ( G ( x ) ∧ H ) = ∀ x G ( x ) ∧ H ∃ x ( G ( x ) ∧ H ) = ∃ x G ( x ) ∧ H
量词转化律
¬ ∀ x G ( x ) = ∃ x ¬ G ( x ) ¬ ∃ x G ( x ) = ∀ x ¬ G ( x ) \neg\forall xG(x)=\exists x\neg G(x)\\ \neg\exists xG(x)=\forall x\neg G(x) ¬∀ x G ( x ) = ∃ x ¬ G ( x ) ¬∃ x G ( x ) = ∀ x ¬ G ( x )
量词分配律
∀ x G ( x ) ∧ ∀ x H ( x ) = ∀ x ( G ( x ) ∧ H ( x ) ) ∃ x G ( x ) ∨ ∃ x H ( x ) = ∃ x ( G ( x ) ∨ H ( x ) ) \forall xG(x)\wedge\forall xH(x)=\forall x(G(x)\wedge H(x))\\ \exists xG(x)\vee\exists xH(x)=\exists x(G(x)\vee H(x)) ∀ x G ( x ) ∧ ∀ x H ( x ) = ∀ x ( G ( x ) ∧ H ( x )) ∃ x G ( x ) ∨ ∃ x H ( x ) = ∃ x ( G ( x ) ∨ H ( x ))
量词分配律(改名)
∀ x G ( x ) ∨ ∀ x H ( x ) = ∀ x ∀ y ( G ( x ) ∨ H ( y ) ) ∃ x G ( x ) ∧ ∃ x H ( x ) = ∃ x ∃ y ( G ( x ) ∧ H ( y ) ) \forall xG(x)\vee\forall xH(x)=\forall x\forall y(G(x)\vee H(y))\\ \exists xG(x)\wedge\exists xH(x)=\exists x\exists y(G(x)\wedge H(y)) ∀ x G ( x ) ∨ ∀ x H ( x ) = ∀ x ∀ y ( G ( x ) ∨ H ( y )) ∃ x G ( x ) ∧ ∃ x H ( x ) = ∃ x ∃ y ( G ( x ) ∧ H ( y ))
定律
基本蕴涵式
量词分配律
∃ x ( A ( x ) ∧ B ( x ) ) ⇒ ∃ x A ( x ) ∧ ∃ y B ( y ) ∀ x A ( x ) ∨ ∀ y B ( y ) ⇒ ∀ x ( A ( x ) ∨ B ( x ) ) ∀ x ( A ( x ) → B ( x ) ) ⇒ ∀ x A ( x ) → ∀ x B ( x ) \exists x(A(x)\wedge B(x))\Rightarrow\exists xA(x)\wedge\exists yB(y)\\ \forall xA(x)\vee\forall yB(y)\Rightarrow\forall x(A(x)\vee B(x))\\ \forall x(A(x)\rightarrow B(x))\Rightarrow\forall xA(x)\rightarrow\forall xB(x) ∃ x ( A ( x ) ∧ B ( x )) ⇒ ∃ x A ( x ) ∧ ∃ y B ( y ) ∀ x A ( x ) ∨ ∀ y B ( y ) ⇒ ∀ x ( A ( x ) ∨ B ( x )) ∀ x ( A ( x ) → B ( x )) ⇒ ∀ x A ( x ) → ∀ x B ( x )
对于谓词公式 A , B A,B A , B A ⇒ B A\Rightarrow B A ⇒ B
方法一: 证明 A → B A\rightarrow B A → B
例:证明 ∃ x ∃ y ( A ( x ) ∧ B ( y ) ) ⇒ ∃ x A ( x ) \exists x\exists y(A(x)\wedge B(y))\Rightarrow\exists xA(x) ∃ x ∃ y ( A ( x ) ∧ B ( y )) ⇒ ∃ x A ( x )
只需证明 ∃ x ∃ y ( A ( x ) ∧ B ( y ) ) → ∃ x A ( x ) \exists x\exists y(A(x)\wedge B(y))\rightarrow\exists xA(x) ∃ x ∃ y ( A ( x ) ∧ B ( y )) → ∃ x A ( x )
∃ x ∃ y ( A ( x ) ∧ B ( y ) ) → ∃ x A ( x ) = ∃ x A ( x ) ∧ ∃ y B ( y ) → ∃ x A ( x ) = ¬ ∃ x A ( x ) ∨ ¬ ∃ y B ( y ) ∨ ∃ x A ( x ) = ( ¬ ∃ x A ( x ) ∨ ∃ x A ( x ) ) ∨ ¬ ∃ y B ( y ) = 1 ∨ ¬ ∃ y B ( y ) = 1 \begin{aligned}
&\quad\exists x\exists y(A(x)\wedge B(y))\rightarrow\exists xA(x)\\
&=\exists xA(x)\wedge\exists yB(y)\rightarrow\exists xA(x)\\
&=\neg\exists xA(x)\vee\neg\exists yB(y)\vee\exists xA(x)\\
&=(\neg\exists xA(x)\vee\exists xA(x))\vee\neg\exists yB(y)\\
&=1\vee\neg\exists yB(y)\\
&=1
\end{aligned} ∃ x ∃ y ( A ( x ) ∧ B ( y )) → ∃ x A ( x ) = ∃ x A ( x ) ∧ ∃ y B ( y ) → ∃ x A ( x ) = ¬∃ x A ( x ) ∨ ¬∃ y B ( y ) ∨ ∃ x A ( x ) = ( ¬∃ x A ( x ) ∨ ∃ x A ( x )) ∨ ¬∃ y B ( y ) = 1 ∨ ¬∃ y B ( y ) = 1
方法二: 由基本等价式和基本蕴涵式推导出 A ⇒ B A\Rightarrow B A ⇒ B
例:证明 ( ∃ x A ( x ) → ∀ x B ( x ) ) ⇒ ∀ x ( A ( x ) → B ( x ) ) (\exists xA(x)\rightarrow\forall xB(x))\Rightarrow\forall x(A(x)\rightarrow B(x)) ( ∃ x A ( x ) → ∀ x B ( x )) ⇒ ∀ x ( A ( x ) → B ( x ))
∃ x A ( x ) → ∀ x B ( x ) = ¬ ∃ x A ( x ) ∨ ∀ x B ( x ) = ∀ x ( ¬ A ( x ) ) ∨ ∀ x B ( x ) ⇒ ∀ x ( ¬ A ( x ) ∨ B ( x ) ) = ∀ x ( A ( x ) → B ( x ) ) \begin{aligned}
\exists xA(x)\rightarrow\forall xB(x)&=\neg\exists xA(x)\vee\forall xB(x)\\
&=\forall x(\neg A(x))\vee\forall xB(x)\\
&\Rightarrow\forall x(\neg A(x)\vee B(x))\\
&=\forall x(A(x)\rightarrow B(x))
\end{aligned} ∃ x A ( x ) → ∀ x B ( x ) = ¬∃ x A ( x ) ∨ ∀ x B ( x ) = ∀ x ( ¬ A ( x )) ∨ ∀ x B ( x ) ⇒ ∀ x ( ¬ A ( x ) ∨ B ( x )) = ∀ x ( A ( x ) → B ( x ))
方法三: 任取解释 I I I I I I A A A I I I B B B
方法四: 证明 ¬ B ⇒ ¬ A \neg B\Rightarrow\neg A ¬ B ⇒ ¬ A
例:证明 ∃ x ( A ( x ) ∨ B ( x ) ) ⇒ ∀ x A ( x ) ∨ ∃ x B ( x ) \exists x(A(x)\vee B(x))\Rightarrow\forall xA(x)\vee\exists xB(x) ∃ x ( A ( x ) ∨ B ( x )) ⇒ ∀ x A ( x ) ∨ ∃ x B ( x )
证法一(方法三):任取解释 I I I ∃ x ( A ( x ) ∨ B ( x ) ) \exists x(A(x)\vee B(x)) ∃ x ( A ( x ) ∨ B ( x )) I I I D D D x x x A ( x ) ∨ B ( x ) A(x)\vee B(x) A ( x ) ∨ B ( x )
若对 D D D x 0 x_0 x 0 B ( x 0 ) B(x_0) B ( x 0 ) ∃ x 0 B ( x 0 ) \exists x_0B(x_0) ∃ x 0 B ( x 0 ) ∀ x 0 A ( x 0 ) ∨ ∃ x 0 B ( x 0 ) \forall x_0A(x_0)\vee\exists x_0B(x_0) ∀ x 0 A ( x 0 ) ∨ ∃ x 0 B ( x 0 )
若对 D D D x x x B ( x ) B(x) B ( x ) A ( x ) A(x) A ( x ) ∀ x A ( x ) \forall xA(x) ∀ x A ( x ) ∀ x 0 A ( x 0 ) ∨ ∃ x 0 B ( x 0 ) \forall x_0A(x_0)\vee\exists x_0B(x_0) ∀ x 0 A ( x 0 ) ∨ ∃ x 0 B ( x 0 )
综上所述,可推得 ∃ x ( A ( x ) ∨ B ( x ) ) ⇒ ∀ x A ( x ) ∨ ∃ x B ( x ) \exists x(A(x)\vee B(x))\Rightarrow\forall xA(x)\vee\exists xB(x) ∃ x ( A ( x ) ∨ B ( x )) ⇒ ∀ x A ( x ) ∨ ∃ x B ( x )
证法二(方法四):假设存在解释 I I I ∃ x ( A ( x ) ∨ B ( x ) ) \exists x(A(x)\vee B(x)) ∃ x ( A ( x ) ∨ B ( x )) ∀ x A ( x ) \forall xA(x) ∀ x A ( x ) ∃ x B ( x ) \exists xB(x) ∃ x B ( x ) D D D x 0 x_0 x 0 A ( x 0 ) A(x_0) A ( x 0 ) D D D x x x B ( x ) B(x) B ( x ) A ( x 0 ) ∨ B ( x 0 ) A(x_0)\vee B(x_0) A ( x 0 ) ∨ B ( x 0 ) ∃ x ( A ( x ) ∨ B ( x ) ) \exists x(A(x)\vee B(x)) ∃ x ( A ( x ) ∨ B ( x )) I I I
因此,∃ x ( A ( x ) ∨ B ( x ) ) ⇒ ∀ x A ( x ) ∨ ∃ x B ( x ) \exists x(A(x)\vee B(x))\Rightarrow\forall xA(x)\vee\exists xB(x) ∃ x ( A ( x ) ∨ B ( x )) ⇒ ∀ x A ( x ) ∨ ∃ x B ( x )
前束范式
如果量词均在公式的开头,并且它们的作用域延伸到整个公式的末端,则该公式被称作前束范式(prenex normal form) ,它的形式如下:
Q 1 x 1 Q 2 x 2 ⋯ Q n x n M , i = 1 , 2 , ⋯ , n Q_1x_1Q_2x_2\cdots Q_nx_nM,\quad i=1,2,\cdots,n
Q 1 x 1 Q 2 x 2 ⋯ Q n x n M , i = 1 , 2 , ⋯ , n
其中 Q i x i Q_ix_i Q i x i ∀ x i \forall x_i ∀ x i ∃ x i \exists x_i ∃ x i M M M Q 1 x 1 Q 2 x 2 ⋯ Q n x n Q_1x_1Q_2x_2\cdots Q_nx_n Q 1 x 1 Q 2 x 2 ⋯ Q n x n 首标 ,将 M M M 母式 。
定理: 对任何公式 G G G
通过如下算法,可将公式 G G G
使用基本等价式,将 G G G ↔ \leftrightarrow ↔ → \rightarrow →
( K ↔ H ) = ( K → H ) ∧ ( H → K ) ( K → H ) = ¬ K ∨ H \begin{aligned}(K\leftrightarrow H)&=(K\rightarrow H)\wedge(H\rightarrow K)\\
(K\rightarrow H)&=\neg K\vee H\end{aligned} ( K ↔ H ) ( K → H ) = ( K → H ) ∧ ( H → K ) = ¬ K ∨ H
使用 ¬ ( ¬ H ) = H \neg(\neg H)=H ¬ ( ¬ H ) = H G G G ¬ \neg ¬
如果必要的话,对约束变元进行改名。
使用量词辖域扩张与分配律将所有量词都提到 G G G
Skolem(斯科伦)范式
如果公式 G G G 可满足性等价(并不一定等价) 的公式 S S S G G G Skolem 化(Skolemization) ,消除存在量词后得到的公式 S S S Skolem 范式(Skolem normal form) 。
所谓可满足性等价,可以理解为以下两点:
满足 S S S G G G
满足 G G G 适当扩充后 可满足 S S S
设 Q 1 x 1 Q 2 x 2 ⋯ Q n x n M Q_1x_1Q_2x_2\cdots Q_nx_nM Q 1 x 1 Q 2 x 2 ⋯ Q n x n M G G G M M M G G G
若 Q r Q_r Q r M M M c c c c c c M M M x r x_r x r Q r x r Q_rx_r Q r x r
若 Q s 1 , Q s 2 , ⋯ , Q s m ( m ≥ 1 , 1 ≤ s 1 < s 2 < ⋯ < s m < r ) Q_{s_1},Q_{s_2},\cdots,Q_{s_m}\ (m\geq 1,1\leq s_1<s_2<\cdots<s_m<r) Q s 1 , Q s 2 , ⋯ , Q s m ( m ≥ 1 , 1 ≤ s 1 < s 2 < ⋯ < s m < r ) Q r x r Q_rx_r Q r x r M M M m m m f ( x s 1 , x s 2 , ⋯ , x s m ) f(x_{s_1},x_{s_2},\cdots,x_{s_m}) f ( x s 1 , x s 2 , ⋯ , x s m ) M M M x r x_r x r Q r x r Q_rx_r Q r x r
用于代替 x r x_r x r G G G Skolem 函数 。
例:将下面公式化为 Skolem 范式:
∀ x ∀ y ( A ( x ) → B ( x , y ) ) → ( ∃ y C ( y ) → ∃ z D ( z ) ) \forall x\forall y(A(x)\to B(x,y))\to(\exists yC(y)\to\exists zD(z))
∀ x ∀ y ( A ( x ) → B ( x , y )) → ( ∃ y C ( y ) → ∃ zD ( z ))
先将其化成母式为合取范式的前束范式:
∃ x ∃ y ∀ t ∃ z [ ( A ( x ) ∨ ¬ C ( t ) ∨ D ( z ) ) ∧ ( ¬ B ( x , y ) ∨ ¬ C ( t ) ∨ D ( z ) ) ] \exists x\exists y\forall t\exists z[(A(x)\vee\neg C(t)\vee D(z))\wedge(\neg B(x,y)\vee\neg C(t)\vee D(z))]
∃ x ∃ y ∀ t ∃ z [( A ( x ) ∨ ¬ C ( t ) ∨ D ( z )) ∧ ( ¬ B ( x , y ) ∨ ¬ C ( t ) ∨ D ( z ))]
用 a a a x x x b b b y y y f ( t ) f(t) f ( t ) z z z
∀ t [ ( A ( a ) ∨ ¬ C ( t ) ∨ D ( f ( t ) ) ) ∧ ( ¬ B ( a , b ) ∨ ¬ C ( t ) ∨ ( f ( t ) ) ) ] \forall t[(A(a)\vee\neg C(t)\vee D(f(t)))\wedge(\neg B(a,b)\vee\neg C(t)\vee(f(t)))]
∀ t [( A ( a ) ∨ ¬ C ( t ) ∨ D ( f ( t ))) ∧ ( ¬ B ( a , b ) ∨ ¬ C ( t ) ∨ ( f ( t )))]
定理: 设 S S S G G G G G G S S S
证明:
假设 G G G S S S G G G S S S G G G S S S G G G G G G S S S G G G
故该定理成立。
例:假设 ∃ x ∀ y M ( x , y ) \exists x\forall yM(x,y) ∃ x ∀ y M ( x , y ) G G G M ( x , y ) M(x,y) M ( x , y ) x , y x,y x , y f f f M ( x , y ) M(x,y) M ( x , y ) G G G ∃ x M ( x , f ( x ) ) \exists xM(x,f(x)) ∃ x M ( x , f ( x ))
分析:要证明 G G G ∃ x M ( x , f ( x ) ) \exists xM(x,f(x)) ∃ x M ( x , f ( x )) ¬ G \neg G ¬ G ¬ ∃ x M ( x , f ( x ) ) \neg\exists xM(x,f(x)) ¬∃ x M ( x , f ( x ))
证:因为
¬ G = ∀ x ∃ y ( ¬ M ( x , y ) ) ¬ ∃ x M ( x , f ( x ) ) = ∀ x ( ¬ M ( x , f ( x ) ) ) \begin{aligned}
\neg G&=\forall x\exists y(\neg M(x,y))\\
\neg\exists xM(x,f(x))&=\forall x(\neg M(x,f(x)))
\end{aligned} ¬ G ¬∃ x M ( x , f ( x )) = ∀ x ∃ y ( ¬ M ( x , y )) = ∀ x ( ¬ M ( x , f ( x )))
又因为 ∀ x ( ¬ M ( x , f ( x ) ) ) \forall x(\neg M(x,f(x))) ∀ x ( ¬ M ( x , f ( x ))) ¬ G \neg G ¬ G
高阶逻辑概述
在之前,我们所使用的谓词逻辑都处在一阶逻辑 系统下,但一些命题并不能用一阶逻辑来确切表述。例如:设 G ( x ) G(x) G ( x ) G ( x ) G(x) G ( x ) ∀ x G ( x ) \forall xG(x) ∀ x G ( x ) ∀ G ( ∀ x G ( x ) ) \forall G(\forall xG(x)) ∀ G ( ∀ x G ( x )) 高阶逻辑 命题。
在公式 ∀ G ( ∀ x G ( x ) ) \forall G(\forall xG(x)) ∀ G ( ∀ x G ( x )) x x x 关于谓词符号的量词 ,由这样的公式所组成的逻辑系统就被称为高阶逻辑。在高阶逻辑中,不仅判定问题不可解,甚至连一个完备的公理系统都没有。
集合代数
集合论所讨论和研究的对象是集合(set) ,所谓集合,是我们将一系列客体的总和而考虑为的一个整体,这些客体叫作该集合的元素(element) ,若有一个集合 A A A a a a A A A a a a a ∈ A a\in A a ∈ A
集合的性质:
确定性:任何一个对象,要么是这个集合的元素,要么不是。
互异性:集合中不允许出现重复的元素。
无序性:我们不考虑集合中元素的顺序。
多样性:集合中的元素可以是任意的对象,相互独立,不要求一定要具备明显的相同特征。
集合的常见定义:
空集(empty set):一个没有任何元素的集合,记作 ∅ \emptyset ∅ ∅ \varnothing ∅ { } \{\} { }
全集(univerasal set):所讨论的对象的全体组成的集合,记作 E E E U U U
有限集(finite set):包含有限个元素的集合,元素数(基数)表示为 ∣ A ∣ |A| ∣ A ∣
无限集(finite set):包含无限个元素的集合。
相等集合:当两个集合所包含的元素完全一样,则称这两个集合相等。
子集(subset):设 A , B A,B A , B A A A B B B A A A B B B A A A B B B A ⊆ B A\subseteq B A ⊆ B
真子集(proper subset):设 A , B A,B A , B A ⊆ B A\subseteq B A ⊆ B A ≠ B A\neq B A = B A A A B B B A A A B B B A ⊂ B A\subset B A ⊂ B
常见的集合表示法:
列举法:将集合中的元素一一列举,或列出足够多的元素以反映集合中元素的特征。
描述法:通过描述集合中元素的共同特征来表示集合:
A = { x ∣ x 的特征 } A=\{x|x的特征\}
A = { x ∣ x 的特征 }
文氏图(又称韦恩图,Venn diagram):
康托尔的朴素集合论公理
1. 外延公理:
2. 抽象公理:
3. 选择公理:
康托尔的朴素集合论公理看上去很美好,但是罗素悖论(Russell’s paradox) 的出现推翻了抽象公理,这里不作过多介绍。
集合的运算
1. 交集(intersection): A , B A,B A , B A A A B B B A A A B B B
A ∩ B = { x ∣ x ∈ A ∧ x ∈ B } A\cap B=\{x|x\in A\wedge x\in B\}
A ∩ B = { x ∣ x ∈ A ∧ x ∈ B }
2. 并集(union): A , B A,B A , B A A A B B B A A A B B B
A ∪ B = { x ∣ x ∈ A ∨ x ∈ B } A\cup B=\{x|x\in A\vee x\in B\}
A ∪ B = { x ∣ x ∈ A ∨ x ∈ B }
并集和交集拥有对应的推广运算:
设 A 1 , A 2 , ⋯ , A n A_1,A_2,\cdots,A_n A 1 , A 2 , ⋯ , A n n n n
A 1 ∪ A 2 ∪ ⋯ ∪ A n ⇔ ⋃ i = 1 n A i A_1\cup A_2\cup\cdots\cup A_n\Leftrightarrow\bigcup_{i=1}^nA_i
A 1 ∪ A 2 ∪ ⋯ ∪ A n ⇔ i = 1 ⋃ n A i
A 1 ∩ A 2 ∩ ⋯ ∩ A n ⇔ ⋂ i = 1 n A i A_1\cap A_2\cap\cdots\cap A_n\Leftrightarrow\bigcap_{i=1}^nA_i
A 1 ∩ A 2 ∩ ⋯ ∩ A n ⇔ i = 1 ⋂ n A i
3. 差集(difference): A , B A,B A , B A A A B B B A A A B B B
A − B = { x ∣ x ∈ A 且 x ∉ B } A-B=\{x|x\in A\ 且\ x\notin B\}
A − B = { x ∣ x ∈ A 且 x ∈ / B }
4. 补集(complement): A A A E E E A A A A A A A ‾ \overline A A
A ‾ = E − A \overline A = E - A
A = E − A
补集和差集的关系:A − B = A ∩ B ‾ A-B=A\cap\overline B A − B = A ∩ B
5. 对称差(symmetric difference): A , B A,B A , B
A ⊕ B = ( A − B ) ∪ ( B − A ) = ( A ∪ B ) − ( A ∩ B ) A\oplus B=(A-B)\cup(B-A)=(A\cup B)-(A\cap B)
A ⊕ B = ( A − B ) ∪ ( B − A ) = ( A ∪ B ) − ( A ∩ B )
6. 幂集(power set): A A A ρ ( A ) \rho(A) ρ ( A ) 2 A 2^A 2 A
定理: 若 A A A
∣ ρ ( A ) ∣ = C n 0 + C n 1 + ⋯ + C n n = 2 n |\rho(A)|=C_n^0+C_n^1+\cdots+C_n^n=2^n
∣ ρ ( A ) ∣ = C n 0 + C n 1 + ⋯ + C n n = 2 n
推论 1: x ∈ ρ ( A ) x\in\rho(A) x ∈ ρ ( A ) x ⊆ A x\subseteq A x ⊆ A
推论 2: 设 A , B A,B A , B A ⊆ B A\subseteq B A ⊆ B ρ ( A ) ⊆ ρ ( B ) \rho(A)\subseteq\rho(B) ρ ( A ) ⊆ ρ ( B )
基本运算律:
运算律
公式
幂等律
A ∩ A = A A ∪ A = A A\cap A=A\\ A\cup A=A A ∩ A = A A ∪ A = A
交换律
A ∩ B = B ∩ A A ∪ B = B ∪ A A\cap B=B\cap A\\ A\cup B=B\cup A A ∩ B = B ∩ A A ∪ B = B ∪ A
结合律
( A ∩ B ) ∩ C = A ∩ ( B ∩ C ) ( A ∪ B ) ∪ C = A ∪ ( B ∪ C ) (A\cap B)\cap C=A\cap(B\cap C)\\ (A\cup B)\cup C=A\cup(B\cup C) ( A ∩ B ) ∩ C = A ∩ ( B ∩ C ) ( A ∪ B ) ∪ C = A ∪ ( B ∪ C )
分配律
A ∩ ( B ∪ C ) = ( A ∩ B ) ∪ ( A ∩ C ) A ∪ ( B ∩ C ) = ( A ∪ B ) ∩ ( A ∪ C ) A\cap(B\cup C)=(A\cap B)\cup(A\cap C)\\ A\cup(B\cap C)=(A\cup B)\cap(A\cup C) A ∩ ( B ∪ C ) = ( A ∩ B ) ∪ ( A ∩ C ) A ∪ ( B ∩ C ) = ( A ∪ B ) ∩ ( A ∪ C )
吸收律
A ∩ ( A ∪ B ) = A A ∪ ( A ∩ B ) = A A\cap(A\cup B)=A\\ A\cup(A\cap B)=A A ∩ ( A ∪ B ) = A A ∪ ( A ∩ B ) = A
互补律
A ∩ A ‾ = ∅ A ∪ A ‾ = E A\cap\overline A=\emptyset\\ A\cup\overline A=E A ∩ A = ∅ A ∪ A = E
De Morgan 律
( A ∩ B ) ‾ = A ‾ ∪ B ‾ ( A ∪ B ) ‾ = A ‾ ∩ B ‾ \overline{(A\cap B)}=\overline A\cup\overline B\\ \overline{(A\cup B)}=\overline A\cap\overline B ( A ∩ B ) = A ∪ B ( A ∪ B ) = A ∩ B
同一律
E ∩ A = A ∅ ∪ A = A E\cap A=A\\ \emptyset\cup A=A E ∩ A = A ∅ ∪ A = A
零一律
∅ ∩ A = ∅ E ∪ A = E \emptyset\cap A=\emptyset\\ E\cup A=E ∅ ∩ A = ∅ E ∪ A = E
双重否定律
A ‾ ‾ = A \overline{\overline A}=A A = A
与集合有关的证明
证明集合的包含关系:
利用上面我们所了解的集合基本概念,我们可以尝试证明集合的包含关系,常见的有以下几种证法:
方法一: 利用定义来证明集合的包含关系。
要证明 A ⊆ B A\subseteq B A ⊆ B x ∈ A x\in A x ∈ A x ∈ B x\in B x ∈ B A A A x ∈ A x\in A x ∈ A x ∈ B x\in B x ∈ B x x x 是任取的 就至关重要。
方法二: 利用包含关系的传递性。
设法找到一个集合 T T T A ⊆ T A\subseteq T A ⊆ T T ⊆ B T\subseteq B T ⊆ B A ⊆ B A\subseteq B A ⊆ B
方法三: 利用 A ⊆ B A\subseteq B A ⊆ B
A ∪ B = B ⟺ A ∩ B = A ⟺ A − B = ∅ A\cup B=B\iff A\cap B=A\iff A-B=\emptyset
A ∪ B = B ⟺ A ∩ B = A ⟺ A − B = ∅
方法四: 利用已知包含式的并、交等运算符得到新的包含式。
例:证明若 A ∩ C ⊆ B ∩ C A\cap C\subseteq B\cap C A ∩ C ⊆ B ∩ C A − C ⊆ B − C A-C\subseteq B-C A − C ⊆ B − C A ⊆ B A\subseteq B A ⊆ B
证:
( A ∩ C ) ∪ ( A − C ) ⊆ ( B ∩ C ) ∪ ( B − C ) ( A ∩ C ) ∪ ( A ∩ C ‾ ) ⊆ ( B ∩ C ) ∪ ( B ∩ C ‾ ) A ∩ ( C ∩ C ‾ ) ⊆ B ∩ ( C ∩ C ‾ ) A ∩ E ⊆ B ∩ E A ⊆ B \begin{aligned}
(A\cap C)\cup(A-C)&\subseteq(B\cap C)\cup(B-C)\\
(A\cap C)\cup(A\cap\overline C)&\subseteq(B\cap C)\cup(B\cap\overline C)\\
A\cap(C\cap\overline C)&\subseteq B\cap(C\cap\overline C)\\
A\cap E&\subseteq B\cap E\\
A&\subseteq B
\end{aligned} ( A ∩ C ) ∪ ( A − C ) ( A ∩ C ) ∪ ( A ∩ C ) A ∩ ( C ∩ C ) A ∩ E A ⊆ ( B ∩ C ) ∪ ( B − C ) ⊆ ( B ∩ C ) ∪ ( B ∩ C ) ⊆ B ∩ ( C ∩ C ) ⊆ B ∩ E ⊆ B
方法五: 反证法:
例:证明若 A ∩ C ⊆ B ∩ C A\cap C\subseteq B\cap C A ∩ C ⊆ B ∩ C A − C ⊆ B − C A-C\subseteq B-C A − C ⊆ B − C A ⊆ B A\subseteq B A ⊆ B
证:若不然,则有 x ∈ A x\in A x ∈ A x ∉ B x\notin B x ∈ / B x ∈ C x\in C x ∈ C x ∈ A ∩ C x\in A\cap C x ∈ A ∩ C x ∉ B ∩ C x\notin B\cap C x ∈ / B ∩ C A ∩ C ⊆ B ∩ C A\cap C\subseteq B\cap C A ∩ C ⊆ B ∩ C x ∉ C x\notin C x ∈ / C x ∈ A − C x\in A-C x ∈ A − C x ∉ B − C x\notin B-C x ∈ / B − C A − C ⊆ B − C A-C\subseteq B-C A − C ⊆ B − C A ⊆ B A\subseteq B A ⊆ B
证明集合的相等关系:
方法一: 利用定义来证明集合的相等关系。
若 A , B A,B A , B A = B A=B A = B A , B A,B A , B A ⊆ B ∧ B ⊆ A A\subseteq B\wedge B\subseteq A A ⊆ B ∧ B ⊆ A
方法二: 反证法。
方法三: 利用集合算律和集合等式。
利用集合的基本算律以及已证明的集合等式,通过相等变换将待证明的等式左(右)边的集合化到右(左)边的集合,或者两边同时相等变换到同一集合。
二元关系
有序对与笛卡尔积
在介绍二元关系之前,我们首先来了解一下有序n元组(ordered n-tuples) ,按一定顺序依次给出 n n n x 1 , x 2 , ⋯ , x n x_1,x_2,\cdots,x_n x 1 , x 2 , ⋯ , x n ( x 1 , x 2 , ⋯ , x n ) (x_1,x_2,\cdots,x_n) ( x 1 , x 2 , ⋯ , x n )
两个有序n元组 ( x 1 , x 2 , ⋯ , x n ) (x_1,x_2,\cdots,x_n) ( x 1 , x 2 , ⋯ , x n ) ( y 1 , y 2 , ⋯ , y n ) (y_1,y_2,\cdots,y_n) ( y 1 , y 2 , ⋯ , y n ) i ∈ { 1 , 2 , ⋯ , n } i\in\{1,2,\cdots,n\} i ∈ { 1 , 2 , ⋯ , n } x i = y i x_i=y_i x i = y i
对于有序n元组,当 n = 2 n=2 n = 2 有序二元组 ,也称作有序对 或序偶 。若 a ≠ b a\neq b a = b ( a , b ) ≠ ( b , a ) (a,b)\neq(b,a) ( a , b ) = ( b , a ) ( a , b ) (a,b) ( a , b ) ( b , a ) (b,a) ( b , a ) a = c , b = d a=c,b=d a = c , b = d
笛卡尔积:
有了有序对的概念,接下来我们引入一种新的运算,称作笛卡尔积 或直积 ,下面这种运算被称作二元笛卡尔积:
A × B = { ( x , y ) ∣ x ∈ A ∧ y ∈ B } A\times B=\{(x,y)|x\in A\wedge y\in B\}
A × B = {( x , y ) ∣ x ∈ A ∧ y ∈ B }
同理还有三元笛卡尔积等等:
A × B × C = { ( x , y , z ) ∣ x ∈ A ∧ y ∈ B ∧ z ∈ C } A\times B\times C=\{(x,y,z)|x\in A\wedge y\in B\wedge z\in C\}
A × B × C = {( x , y , z ) ∣ x ∈ A ∧ y ∈ B ∧ z ∈ C }
下面我们所说的笛卡尔积皆为二元笛卡尔积。
笛卡尔积有以下性质:
若 ∣ A ∣ = m , ∣ B ∣ = b |A|=m,|B|=b ∣ A ∣ = m , ∣ B ∣ = b ∣ A × B ∣ = ∣ A ∣ × ∣ B ∣ = m n |A\times B|=|A|\times|B|=mn ∣ A × B ∣ = ∣ A ∣ × ∣ B ∣ = mn
对任意集合 A A A A × ∅ = ∅ A\times\emptyset=\emptyset A × ∅ = ∅ ∅ × A = ∅ \emptyset\times A=\emptyset ∅ × A = ∅
笛卡尔积不满足交换律,即 A × B ≠ B × A A\times B\neq B\times A A × B = B × A
笛卡尔积不满足结合律,即 ( A × B ) × C ≠ A × ( B × C ) (A\times B)\times C\neq A\times(B\times C) ( A × B ) × C = A × ( B × C )
直积运算对并和交运算满足分配律:
A × ( B × C ) = ( A × B ) ∪ ( A × C ) ( B ∪ C ) × A = ( B × A ) ∪ ( C × A ) A × ( B ∩ C ) = ( A × B ) ∩ ( A × C ) ( B ∩ C ) × A = ( B × A ) ∩ ( C × A ) A\times(B\times C)=(A\times B)\cup(A\times C)\\
(B\cup C)\times A=(B\times A)\cup(C\times A)\\
A\times(B\cap C)=(A\times B)\cap(A\times C)\\
(B\cap C)\times A=(B\times A)\cap(C\times A) A × ( B × C ) = ( A × B ) ∪ ( A × C ) ( B ∪ C ) × A = ( B × A ) ∪ ( C × A ) A × ( B ∩ C ) = ( A × B ) ∩ ( A × C ) ( B ∩ C ) × A = ( B × A ) ∩ ( C × A )
设 A , B , C , D A,B,C,D A , B , C , D A ⊆ C A\subseteq C A ⊆ C B ⊆ D B\subseteq D B ⊆ D A × B ⊆ C × D A\times B\subseteq C\times D A × B ⊆ C × D
关系的定义
设 A 1 , A 2 , ⋯ , A n A_1,A_2,\cdots,A_n A 1 , A 2 , ⋯ , A n n n n A 1 × A 2 × ⋯ × A n A_1\times A_2\times\cdots\times A_n A 1 × A 2 × ⋯ × A n F F F A 1 , A 2 , ⋯ , A n A_1,A_2,\cdots,A_n A 1 , A 2 , ⋯ , A n n \bm n n 元关系 。
特别地,集合 A × B A\times B A × B R R R A A A B B B 二元关系 ,简称为关系 。
对于 x ∈ A , y ∈ B x\in A,y\in B x ∈ A , y ∈ B
若 ( x , y ) ∈ R (x,y)\in R ( x , y ) ∈ R x , y x,y x , y R R R x R y xRy x R y
若 ( x , y ) ∉ R (x,y)\notin R ( x , y ) ∈ / R x , y x,y x , y R R R x R y x\cancel Ry x R y
A \bm A A
若 A = B A=B A = B R R R A A A
A × A A\times A A × A A A A 若 ∣ A ∣ = n |A|=n ∣ A ∣ = n A A A 2 n 2 2^{n^2} 2 n 2
A A A ∅ \emptyset ∅ E A = A × A E_A=A\times A E A = A × A I A = { ( x , x ) ∣ x ∈ A } I_A=\{(x,x)|x\in A\} I A = {( x , x ) ∣ x ∈ A } R ‾ = E A − R = A × A − R \overline R=E_A-R=A\times A-R R = E A − R = A × A − R
关系的表示法
集合表示法: 直接使用定义,这种表示法便于书写。
例:设 A = { 1 , 2 , 3 , 4 } A=\{1,2,3,4\} A = { 1 , 2 , 3 , 4 } A A A
R = { ( 1 , 1 ) , ( 1 , 2 ) , ( 1 , 3 ) , ( 2 , 1 ) , ( 2 , 2 ) } R=\{(1,1),(1,2),(1,3),(2,1),(2,2)\}
R = {( 1 , 1 ) , ( 1 , 2 ) , ( 1 , 3 ) , ( 2 , 1 ) , ( 2 , 2 )}
关系矩阵(relation matrix)表示法: 这种表示法便于存储。
给定两个有限集合 A = { a 1 , ⋯ , a m } , B = { b 1 , ⋯ , b n } A=\{a_1,\cdots,a_m\},B=\{b_1,\cdots,b_n\} A = { a 1 , ⋯ , a m } , B = { b 1 , ⋯ , b n } R R R A A A B B B M R = [ r i j ] m × n M_R=[r_{ij}]_{m\times n} M R = [ r ij ] m × n R R R
[ r 11 r 12 ⋯ r 1 n r 21 r 22 ⋯ r 2 n ⋮ ⋮ ⋮ r m 1 r m 2 ⋯ r m n ] \begin{bmatrix}
r_{11}&r_{12}&\cdots&r_{1n}\\
r_{21}&r_{22}&\cdots&r_{2n}\\
\vdots&\vdots&&\vdots\\
r_{m1}&r_{m2}&\cdots&r_{mn}
\end{bmatrix} r 11 r 21 ⋮ r m 1 r 12 r 22 ⋮ r m 2 ⋯ ⋯ ⋯ r 1 n r 2 n ⋮ r mn
其中若 ( a i , b j ) ∈ R (a_i,b_j)\in R ( a i , b j ) ∈ R r i j = 1 r_{ij}=1 r ij = 1 r i j = 0 r_{ij}=0 r ij = 0
关系矩阵表示与矩阵的行列对应的集合。
关系图(digraph of relations)表示法: 这种表示法较为直观清晰。
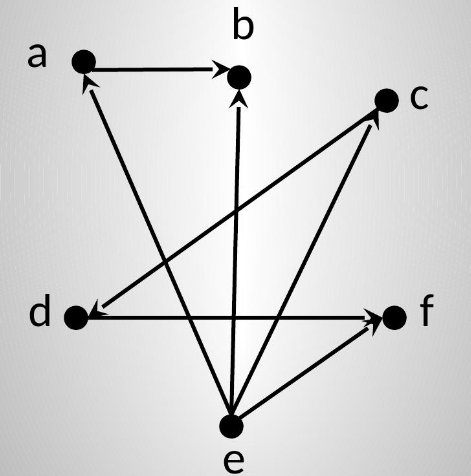
给定两个有限集合 A = { a 1 , ⋯ , a m } , B = { b 1 , ⋯ , b n } A=\{a_1,\cdots,a_m\},B=\{b_1,\cdots,b_n\} A = { a 1 , ⋯ , a m } , B = { b 1 , ⋯ , b n } R R R A A A B B B
首先在平面上作 m m m a 1 , ⋯ , a m a_1,\cdots,a_m a 1 , ⋯ , a m n n n b 1 , ⋯ , b n b_1,\cdots,b_n b 1 , ⋯ , b n
关系(有向)图常用来表示 A × A A\times A A × A A A A A A A A A A R R R ( a , b ) (a,b) ( a , b ) a a a b b b
关系的运算
关系是集合的一种,所以处理集合的方法对关系都是有效的,因此我们也可以为关系定义一套类似于集合的运算。
1. 关系的交: x , y ∈ A x,y\in A x , y ∈ A
x ( R ∩ S ) y ⟺ ( x , y ) ∈ R ∩ S ⟺ ( x , y ) ∈ R 并且 ( x , y ) ∈ S ⟺ x R y 并且 x S y \begin{aligned}
x(R\cap S)y&\iff(x,y)\in R\cap S\\
&\iff(x,y)\in R\ 并且\ (x,y)\in S\\
&\iff xRy\ 并且\ xSy
\end{aligned} x ( R ∩ S ) y ⟺ ( x , y ) ∈ R ∩ S ⟺ ( x , y ) ∈ R 并且 ( x , y ) ∈ S ⟺ x R y 并且 x S y
R ∩ S = { ( x , y ) ∣ x ∈ A , y ∈ A , x R y ∧ x S y } R\cap S=\{(x,y)|x\in A,y\in A,xRy\wedge xSy\}
R ∩ S = {( x , y ) ∣ x ∈ A , y ∈ A , x R y ∧ x S y }
2. 关系的并: x , y ∈ A x,y\in A x , y ∈ A
x ( R ∪ S ) y ⟺ ( x , y ) ∈ R ∪ S ⟺ ( x , y ) ∈ R 或 ( x , y ) ∈ S ⟺ x R y 或 x S y \begin{aligned}
x(R\cup S)y&\iff(x,y)\in R\cup S\\
&\iff(x,y)\in R\ 或\ (x,y)\in S\\
&\iff xRy\ 或\ xSy
\end{aligned} x ( R ∪ S ) y ⟺ ( x , y ) ∈ R ∪ S ⟺ ( x , y ) ∈ R 或 ( x , y ) ∈ S ⟺ x R y 或 x S y
R ∪ S = { ( x , y ) ∣ x ∈ A , y ∈ A , x R y ∨ x S y } R\cup S=\{(x,y)|x\in A,y\in A,xRy\vee xSy\}
R ∪ S = {( x , y ) ∣ x ∈ A , y ∈ A , x R y ∨ x S y }
3. 关系的差: x , y ∈ A x,y\in A x , y ∈ A
x ( R − S ) y ⟺ ( x , y ) ∈ R − S ⟺ x R y 并且 x S y \begin{aligned}
x(R-S)y&\iff(x,y)\in R-S\\
&\iff xRy\ 并且\ x\cancel Sy
\end{aligned} x ( R − S ) y ⟺ ( x , y ) ∈ R − S ⟺ x R y 并且 x S y
R − S = { ( x , y ) ∣ x ∈ A , y ∈ A , x R y ∧ x S y } R-S=\{(x,y)|x\in A,y\in A,xRy\wedge x\cancel Sy\}
R − S = {( x , y ) ∣ x ∈ A , y ∈ A , x R y ∧ x S y }
4. 关系的余: x , y ∈ A x,y\in A x , y ∈ A
x R ‾ y ⟺ ( x , y ) ∈ R ‾ ⟺ x R y \begin{aligned}
x\overline Ry&\iff(x,y)\in\overline R\\
&\iff x\cancel Ry
\end{aligned} x R y ⟺ ( x , y ) ∈ R ⟺ x R y
R ‾ = A × A − R = { ( x , y ) ∣ x ∈ A , y ∈ A , x R y } \overline R=A\times A-R=\{(x,y)|x\in A,y\in A,x\cancel Ry\}
R = A × A − R = {( x , y ) ∣ x ∈ A , y ∈ A , x R y }
5. 子关系: R , S R,S R , S A A A R ⊆ S R\subseteq S R ⊆ S R R R S S S
从集合的角度:R R R S S S
从关系矩阵的角度:M R M_R M R 1 1 1 M S M_S M S 1 1 1
从关系图的角度:R R R S S S
6. 逆关系: R R R A A A R − 1 R^{-1} R − 1 R R R
R − 1 = { ( y , x ) ∣ x ∈ A , y ∈ A , 并且 x R y } R^{-1}=\{(y,x)|x\in A,y\in A,并且\ xRy\}
R − 1 = {( y , x ) ∣ x ∈ A , y ∈ A , 并且 x R y }
x R − 1 y ⟺ ( x , y ) ∈ R − 1 ⟺ y R x xR^{-1}y\iff(x,y)\in R^{-1}\iff yRx
x R − 1 y ⟺ ( x , y ) ∈ R − 1 ⟺ y R x
从集合的角度:将 R R R R − 1 R^{-1} R − 1
从关系矩阵的角度:M R − 1 M_R^{-1} M R − 1 M R M_R M R
从关系图的角度:将 R R R R − 1 R^{-1} R − 1
7. 关系的乘积: R , S R,S R , S A A A R ⋅ S R\cdot S R ⋅ S R R R S S S
R ⋅ S = { ( x , y ) ∣ x ∈ A , y ∈ A , 并且存在 z ∈ A 使得 x R z , z S y } R\cdot S=\{(x,y)|x\in A,y\in A,并且存在\ z\in A\ 使得\ xRz,zSy\}
R ⋅ S = {( x , y ) ∣ x ∈ A , y ∈ A , 并且存在 z ∈ A 使得 x R z , z S y }
R ⋅ I A = I A ⋅ R = R R\cdot I_A=I_A\cdot R=R
R ⋅ I A = I A ⋅ R = R
从关系矩阵的角度:若对 { 0 , 1 } \{0,1\} { 0 , 1 } A A A R , S R,S R , S
M R ⋅ S = M R ⋅ M S M_{R\cdot S}=M_R\cdot M_S
M R ⋅ S = M R ⋅ M S
从关系图的角度:将 R , S R,S R , S
例:证明 ( R ⋅ S ) ⋅ T ⊆ R ⋅ ( S ⋅ T ) (R\cdot S)\cdot T\subseteq R\cdot(S\cdot T) ( R ⋅ S ) ⋅ T ⊆ R ⋅ ( S ⋅ T )
证:任取 ( x , y ) ∈ ( R ⋅ S ) ⋅ T (x,y)\in(R\cdot S)\cdot T ( x , y ) ∈ ( R ⋅ S ) ⋅ T x ( R ⋅ S ) ⋅ T y x(R\cdot S)\cdot Ty x ( R ⋅ S ) ⋅ T y z ∈ A z\in A z ∈ A
x ( R ⋅ S ) z , z T y x(R\cdot S)z,\quad zTy
x ( R ⋅ S ) z , z T y
同样对 x ( R ⋅ S ) z x(R\cdot S)z x ( R ⋅ S ) z z ′ ∈ A z'\in A z ′ ∈ A
x R z ′ , z ′ S z xRz',\quad z'Sz
x R z ′ , z ′ S z
故由 z ′ S z z'Sz z ′ S z z T y zTy z T y z ′ ( S ⋅ T ) y z'(S\cdot T)y z ′ ( S ⋅ T ) y x R z ′ xRz' x R z ′ x R ⋅ ( S ⋅ T ) y xR\cdot(S\cdot T)y x R ⋅ ( S ⋅ T ) y ( x , y ) ∈ R ⋅ ( S ⋅ T ) (x,y)\in R\cdot(S\cdot T) ( x , y ) ∈ R ⋅ ( S ⋅ T ) ( x , y ) ∈ ( R ⋅ S ) ⋅ T (x,y)\in(R\cdot S)\cdot T ( x , y ) ∈ ( R ⋅ S ) ⋅ T
8. 关系的幂: A A A
R n = R ⋅ R ⋅ ⋯ ⋅ R ⏟ n × R R^n=\underbrace{R\cdot R\cdot\cdots\cdot R}_{n\times R}
R n = n × R R ⋅ R ⋅ ⋯ ⋅ R
关系的幂满足如下定义:
{ R 0 = I A R n + 1 = R n ⋅ R , n ∈ N \left\{\begin{aligned}
&R^0=I_A\\
&R^{n+1}=R^n\cdot R,\quad n\in N
\end{aligned}\right. { R 0 = I A R n + 1 = R n ⋅ R , n ∈ N
关系的幂具有以下基本性质:
设 R R R A A A m , n m,n m , n
R m ⋅ R n = R m + n ( R m ) n = R m n R^m\cdot R^n=R^{m+n}\\
(R^m)^n=R^{mn} R m ⋅ R n = R m + n ( R m ) n = R mn
设集合 A A A n n n R R R A A A i , j ( 0 ≤ i < j ≤ 2 n 2 ) i,j\ (0\leq i<j\leq 2^{n^2}) i , j ( 0 ≤ i < j ≤ 2 n 2 ) R i = R j R^i=R^j R i = R j
设 R R R A A A i , j ( i < j ) i,j\ (i<j) i , j ( i < j ) R i = R j R^i=R^j R i = R j
R i + k = R j + k , k ∈ N R i + k p + m = R i + m , k , m ∈ N , p = j − i R^{i+k}=R^{j+k},\quad k\in N\\
R^{i+kp+m}=R^{i+m},\quad k,m\in N,p=j-i R i + k = R j + k , k ∈ N R i + k p + m = R i + m , k , m ∈ N , p = j − i
证明:R i + k p + m = R i + m R^{i+kp+m}=R^{i+m} R i + k p + m = R i + m k , m ∈ N , p = j − i k,m\in N,p=j-i k , m ∈ N , p = j − i
R i + k p + m = R i + ( j − i ) + ( k − 1 ) ( j − i ) + m = R j + ( k − 1 ) ( j − 1 ) + m = R i + ( k − 1 ) ( j − i ) + m = R i + ( j − i ) + ( k − 2 ) ( j − i ) + m = R j + ( k − 2 ) ( j − i ) + m = R i + ( k − 2 ) ( j − i ) + m ⋮ = R i + ( j − i ) + m = R j + m = R i + m \begin{aligned}
R^{i+kp+m}&=R^{i+(j-i)+(k-1)(j-i)+m}=R^{j+(k-1)(j-1)+m}\\
&=R^{i+(k-1)(j-i)+m}=R^{i+(j-i)+(k-2)(j-i)+m}\\
&=R^{j+(k-2)(j-i)+m}=R^{i+(k-2)(j-i)+m}\\
&\ \ \vdots\\
&=R^{i+(j-i)+m}=R^{j+m}=R^{i+m}
\end{aligned} R i + k p + m = R i + ( j − i ) + ( k − 1 ) ( j − i ) + m = R j + ( k − 1 ) ( j − 1 ) + m = R i + ( k − 1 ) ( j − i ) + m = R i + ( j − i ) + ( k − 2 ) ( j − i ) + m = R j + ( k − 2 ) ( j − i ) + m = R i + ( k − 2 ) ( j − i ) + m ⋮ = R i + ( j − i ) + m = R j + m = R i + m
特殊关系
1. 自反关系(reflexive): A A A R R R x ∈ A x\in A x ∈ A x R x xRx x R x
R R R ⟺ \iff ⟺ I A ⊆ R I_A\subseteq R I A ⊆ R ⟺ \iff ⟺ R − 1 R^{-1} R − 1 从关系矩阵的角度:M R M_R M R
从关系图的角度:R R R
2. 反自反关系(irreflexive): A A A R R R x ∈ A x\in A x ∈ A x R x x\cancel Rx x R x
R R R ⟺ \iff ⟺ I A ∩ R = ∅ I_A\cap R=\emptyset I A ∩ R = ∅ 从关系矩阵的角度:M R M_R M R
从关系图的角度:R R R
3. 对称关系(symmetric): A A A R R R x R y ( x ∈ A , y ∈ A ) xRy\ (x\in A,y\in A) x R y ( x ∈ A , y ∈ A ) y R x yRx y R x
R R R ⟺ \iff ⟺ R − 1 = R R^{-1}=R R − 1 = R 从关系矩阵的角度:M R M_R M R
从关系图的角度:R R R
4. 反对称关系(antisymmetric): A A A R R R x R y , y R x xRy,yRx x R y , y R x x = y x=y x = y x R y , x ≠ y xRy,x\neq y x R y , x = y y R x y\cancel Rx y R x
R R R ⟺ \iff ⟺ R ∩ R − 1 ⊆ I A R\cap R^{-1}\subseteq I_A R ∩ R − 1 ⊆ I A 从关系矩阵的角度:M R M_R M R
从关系图的角度:R R R
5. 传递关系(transitive): A A A R R R x ∈ A , y ∈ A , z ∈ A x\in A,y\in A,z\in A x ∈ A , y ∈ A , z ∈ A x R y , y R z xRy,yRz x R y , y R z x R z xRz x R z
R R R ⟺ \iff ⟺ R 2 ⊆ R R^2\subseteq R R 2 ⊆ R 从关系矩阵的角度:如果 M R 2 M_{R^2} M R 2 s i j = 1 s_{ij}=1 s ij = 1 M R M_R M R r i j r_{ij} r ij
从关系图的角度:R R R a , b , c a,b,c a , b , c a a a b b b b b b c c c a a a c c c
关系名称
拥有的特殊关系
空集上的空关系 ∅ \emptyset ∅
自反、反自反、对称、反对称、传递
非空集合上的空关系 ∅ \emptyset ∅
反自反、对称、反对称、传递
恒等关系 I A ( ∣ A ∣ > 0 ) I_A\ (|A|>0) I A ( ∣ A ∣ > 0 )
自反、对称、反对称、传递
全域关系 E A ( ∣ A ∣ > 1 ) E_A\ (|A|>1) E A ( ∣ A ∣ > 1 )
自反、对称、传递
关系的闭包
所谓闭包,指的就是对原关系的序偶进行一些扩充,使得原关系满足某种特殊性质,并且要求对原关系的改动最小化。
设 A A A R R R A A A R ′ R' R ′ R R R R ′ R' R ′
R ′ R' R ′ R ⊆ R ′ R\subseteq R' R ⊆ R ′ 对 A A A R ′ ′ R'' R ′′ R ⊆ R ′ ′ R\subseteq R'' R ⊆ R ′′ R ′ ′ R'' R ′′ R ′ ⊆ R ′ ′ R'\subseteq R'' R ′ ⊆ R ′′
R R R r ( R ) , s ( R ) , t ( R ) r(R),s(R),t(R) r ( R ) , s ( R ) , t ( R ) r , s , t r,s,t r , s , t 闭包运算 。
闭包定理:
r ( R ) = I A ∪ R r(R)=I_A\cup R r ( R ) = I A ∪ R s ( R ) = R ∪ R − 1 s(R)=R\cup R^{-1} s ( R ) = R ∪ R − 1 t ( R ) = ⋃ i = 1 ∞ R i \displaystyle t(R)=\bigcup_{i=1}^\infty R^i t ( R ) = i = 1 ⋃ ∞ R i R i R^i R i
等价关系与等价类
设 A A A R R R A A A R R R 自反、对称、传递性 ,则称 R R R 等价关系(equivalence relation) ,通常记作 ≅ \cong ≅
设 A A A R R R A A A A A A M M M R R R 等价类 ,其满足
若 a ∈ M , b ∈ M a\in M,b\in M a ∈ M , b ∈ M a R b aRb a R b
若 a ∈ M , b ∉ M a\in M,b\notin M a ∈ M , b ∈ / M a R b a\cancel Rb a R b a ∈ M , a R b a\in M,aRb a ∈ M , a R b b ∈ M b\in M b ∈ M
可以将等价类看作是拥有某一共同特征的元素组成的集合,等价关系即为集合中的元素所拥有的关系。
通常,用 [ a ] R [a]_R [ a ] R a a a a a a 代表元 :
[ a ] R = { x ∣ ( x , a ) ∈ R } [a]_R=\{x|(x,a)\in R\}
[ a ] R = { x ∣ ( x , a ) ∈ R }
定理1: 设 ≅ \cong ≅ A A A
证明:任取 a ∈ A a\in A a ∈ A M = { x ∣ x ∈ A 并且 x ≅ a } M=\{x|x\in A\ \text{并且}\ x\cong a\} M = { x ∣ x ∈ A 并且 x ≅ a }
(1)显然,a ∈ M a\in M a ∈ M M M M
(2)任取 x 1 ∈ M , x 2 ∈ M x_1\in M,x_2\in M x 1 ∈ M , x 2 ∈ M x 1 ≅ a , x 2 ≅ a x_1\cong a,x_2\cong a x 1 ≅ a , x 2 ≅ a ≅ \cong ≅ x 1 ≅ x 2 x_1\cong x_2 x 1 ≅ x 2
(3)任取 x 1 ∈ M x_1\in M x 1 ∈ M x 1 ≅ y x_1\cong y x 1 ≅ y x 1 ≅ a x_1\cong a x 1 ≅ a ≅ \cong ≅ y ≅ a y\cong a y ≅ a y ∈ M y\in M y ∈ M
综上所述,可以认为 M M M ≅ \cong ≅
定理2: 设 ≅ \cong ≅ A A A M 1 , M 2 , ⋯ M_1,M_2,\cdots M 1 , M 2 , ⋯ A A A ≅ \cong ≅
A = M 1 ∪ M 2 ∪ ⋯ A=M_1\cup M_2\cup\cdots
A = M 1 ∪ M 2 ∪ ⋯
并且
M i ∩ M j = ∅ ( i ≠ j ) M_i\cap M_j=\emptyset\quad(i\neq j)
M i ∩ M j = ∅ ( i = j )
换句话说,集合 A A A A A A
证明:
任取 M i , M j , i ≠ j M_i,M_j,i\neq j M i , M j , i = j M i ∩ M j ≠ ∅ M_i\cap M_j\neq\emptyset M i ∩ M j = ∅ x ∈ M i ∩ M j x\in M_i\cap M_j x ∈ M i ∩ M j a ∈ M i a\in M_i a ∈ M i b ∈ M j b\in M_j b ∈ M j a ≅ M i a\cong M_i a ≅ M i b ≅ M j b\cong M_j b ≅ M j a ≅ b a\cong b a ≅ b M i = M j M_i=M_j M i = M j M i ∩ M j = ∅ M_i\cap M_j=\emptyset M i ∩ M j = ∅
任取 a ∈ A a\in A a ∈ A M = { x ∣ x ∈ A 并且 x ≅ a } M=\{x|x\in A\ \text{并且}\ x\cong a\} M = { x ∣ x ∈ A 并且 x ≅ a } M M M k k k M k = M M_k=M M k = M a ∈ M a\in M a ∈ M a ∈ M 1 ∪ M 2 ∪ ⋯ ∪ M k ∪ ⋯ a\in M_1\cup M_2\cup\cdots\cup M_k\cup\cdots a ∈ M 1 ∪ M 2 ∪ ⋯ ∪ M k ∪ ⋯ A ⊆ M 1 ∪ M 2 ∪ ⋯ A\subseteq M_1\cup M_2\cup\cdots A ⊆ M 1 ∪ M 2 ∪ ⋯ M 1 ∪ M 2 ∪ ⋯ ⊆ A M_1\cup M_2\cup\cdots\subseteq A M 1 ∪ M 2 ∪ ⋯ ⊆ A A = M 1 ∪ M 2 ∪ ⋯ A=M_1\cup M_2\cup\cdots A = M 1 ∪ M 2 ∪ ⋯
划分与商集
称集合 A A A 子集族 C C C A A A 划分(partition) ,如果满足以下条件:
若 B ∈ C B\in C B ∈ C B ≠ ∅ B\neq\emptyset B = ∅
⋃ B ∈ C B = A \displaystyle\bigcup_{B\in C}B=A B ∈ C ⋃ B = A 对任意的 B B B B ′ ∈ C B'\in C B ′ ∈ C B ≠ B ′ B\neq B' B = B ′ B ∩ B ′ = ∅ B\cap B'=\emptyset B ∩ B ′ = ∅
则称 C C C 单元 ,或划分块 。
我们规定,A = ∅ A=\emptyset A = ∅ ∅ \emptyset ∅
设 R R R A A A R R R 所有不同等价类为元素 作成的集合称为 A A A R R R 商集(quotient set) ,简称 A A A A / R A/R A / R
划分和等价关系能由以下定理联系在一起:
设 A A A R R R A A A A / R A/R A / R A A A
设 A A A C C C A A A R C = { ( x , y ) ∣ x , y ∈ A 并且 x , y 属于 C 的同一划分块 } R_C=\{(x,y)|x,y\in A\ \text{并且}\ x,y\ \text{属于}\ C\ \text{的同一划分块}\} R C = {( x , y ) ∣ x , y ∈ A 并且 x , y 属于 C 的同一划分块 } R C R_C R C A A A
I A , E A , R i j I_A,E_A,R_{ij} I A , E A , R ij A A A
A / I A = { { a 1 } , { a 2 } , ⋯ , { a n } } A / E A = { { a 1 , a 2 , ⋯ , a n } } A / R i j = { { a i , a j } , { a k 1 } , { a k 2 } , ⋯ , { a k n − 2 } } \begin{aligned}
A/I_A&=\left\{ \{ a_1 \},\{ a_2 \},\cdots,\{ a_n \} \right\}\\
A/E_A&=\left\{ \{ a_1,a_2,\cdots,a_n \} \right\}\\
A/R_{ij}&=\left\{ \{ a_i,a_j \},\{ a_{k_1} \},\{ a_{k_2} \},\cdots,\{ a_{k_{n-2}} \} \right\}
\end{aligned} A / I A A / E A A / R ij = { { a 1 } , { a 2 } , ⋯ , { a n } } = { { a 1 , a 2 , ⋯ , a n } } = { { a i , a j } , { a k 1 } , { a k 2 } , ⋯ , { a k n − 2 } }
其中 k 1 , k 2 , ⋯ , k n − 2 k_1,k_2,\cdots,k_{n-2} k 1 , k 2 , ⋯ , k n − 2 i i i j j j C n 2 C_n^2 C n 2 R i j R_{ij} R ij
等价关系 ⇒ \bm\Rightarrow ⇒ A A A
例:A = { a , b , c } A=\{a,b,c\} A = { a , b , c } A A A I A I_A I A A / I A A/I_A A / I A
I A = { ( a , a ) , ( b , b ) , ( c , c ) } [ a ] I A = a , [ b ] I A = b , [ c ] I A = c A / I A = { { a } , { b } , { c } } \begin{aligned}
&I_A=\{(a,a),(b,b),(c,c)\}\\
&[a]_{I_A}={a},[b]_{I_A}={b},[c]_{I_A}={c}\\
&A/I_A=\left\{\{ a\},\{b\},\{c\}\right\}
\end{aligned} I A = {( a , a ) , ( b , b ) , ( c , c )} [ a ] I A = a , [ b ] I A = b , [ c ] I A = c A / I A = { { a } , { b } , { c } }
商集 ⇒ \bm\Rightarrow ⇒ R = I A ∪ { ( ) , ( ) , ⋯ } R=I_A\cup\{(),(),\cdots\} R = I A ∪ {( ) , ( ) , ⋯ }
例:A = { a , b , c } A=\{a,b,c\} A = { a , b , c } A A A A / R = { { a } , { b , c } } A/R=\left\{\{a\},\{b,c\}\right\} A / R = { { a } , { b , c } } R R R
R = { ( a , a ) , ( b , b ) , ( c , c ) , ( b , c ) , ( c , b ) } = I A ∪ { ( b , c ) , ( c , b ) } \begin{aligned}
R&=\{(a,a),(b,b),(c,c),(b,c),(c,b)\}\\
&=I_A\cup\{(b,c),(c,b)\}
\end{aligned} R = {( a , a ) , ( b , b ) , ( c , c ) , ( b , c ) , ( c , b )} = I A ∪ {( b , c ) , ( c , b )}
划分的加细:
设 C C C C ′ C' C ′ A A A C C C C ′ C' C ′ C C C C ′ C' C ′ 加细(refinement) 。
定理: C C C C ′ C' C ′ R C ⊆ R C ′ R_C\subseteq R_{C'} R C ⊆ R C ′
第二类斯特林(Stirling)数:
第二类斯特林数用于研究将元素划分成若干集合,每个集合非空的方案数,因此又称斯特林子集数 。用 { n m } \begin{Bmatrix}n\\m\end{Bmatrix} { n m } n n n m m m n n n m m m
我们能发现第二类斯特林数的几个特例:
{ n 0 } = 0 , { n 1 } = 1 , { n 2 } = 2 n − 1 − 1 , { n n − 1 } = C n 2 , { n n } = 1 \begin{Bmatrix}n\\0\end{Bmatrix}=0,\begin{Bmatrix}n\\1\end{Bmatrix}=1,\begin{Bmatrix}n\\2\end{Bmatrix}=2^{n-1}-1,\begin{Bmatrix}n\\n-1\end{Bmatrix}=C_n^2,\begin{Bmatrix}n\\n\end{Bmatrix}=1
{ n 0 } = 0 , { n 1 } = 1 , { n 2 } = 2 n − 1 − 1 , { n n − 1 } = C n 2 , { n n } = 1
考虑若 n n n m m m n n n n − 1 n-1 n − 1 m m m
{ n m } = m { n − 1 m } + { n − 1 m − 1 } \begin{Bmatrix}n\\m\end{Bmatrix}=m\begin{Bmatrix}n-1\\m\end{Bmatrix}+\begin{Bmatrix}n-1\\m-1\end{Bmatrix}
{ n m } = m { n − 1 m } + { n − 1 m − 1 }
利用第二类斯特林数求集合的划分个数: A A A n n n
{ n 1 } + { n 2 } + ⋯ + { n n } \begin{Bmatrix}n\\1\end{Bmatrix}+\begin{Bmatrix}n\\2\end{Bmatrix}+\cdots+\begin{Bmatrix}n\\n\end{Bmatrix}
{ n 1 } + { n 2 } + ⋯ + { n n }
序关系
偏序关系:
设 R R R A A A R R R 自反性、反对称性、传递性 ,则称 R R R 偏序关系(partial ordering relation) ,或半序关系 ,部分序关系 ,通常写为 ≤ \leq ≤
集合 A A A R R R 偏序集(partial ordered set,poset) ,或半序集 ,部分序集 ,记作 ( A , R ) (A,R) ( A , R )
一个偏序集的子集仍为偏序集,并且
( A , R ) ⇒ ( B , R ∩ ( B × B ) ) , B ⊆ A (A,R)\Rightarrow(B,R\cap(B\times B)),\quad B\subseteq A
( A , R ) ⇒ ( B , R ∩ ( B × B )) , B ⊆ A
证明:
(1)R ∩ ( B × B ) R\cap(B\times B) R ∩ ( B × B )
任取 x ∈ B x\in B x ∈ B ( x , x ) ∈ B × B (x,x)\in B\times B ( x , x ) ∈ B × B x ∈ B x\in B x ∈ B B ⊆ A B\subseteq A B ⊆ A x ∈ A x\in A x ∈ A R R R A A A ( x , x ) ∈ R (x,x)\in R ( x , x ) ∈ R ( x , x ) ∈ R ∩ ( B × B ) (x,x)\in R\cap(B\times B) ( x , x ) ∈ R ∩ ( B × B ) R ∩ ( B × B ) R\cap(B\times B) R ∩ ( B × B )
(2)R ∩ ( B × B ) R\cap(B\times B) R ∩ ( B × B )
若 ( x , y ) ∈ R ∩ ( B × B ) (x,y)\in R\cap(B\times B) ( x , y ) ∈ R ∩ ( B × B ) ( y , x ) ∈ R ∩ ( B × B ) (y,x)\in R\cap(B\times B) ( y , x ) ∈ R ∩ ( B × B ) ( x , y ) ∈ R (x,y)\in R ( x , y ) ∈ R ( y , x ) ∈ R (y,x)\in R ( y , x ) ∈ R R R R x = y x=y x = y R ∩ ( B × B ) R\cap(B\times B) R ∩ ( B × B )
(3)R ∩ ( B × B ) R\cap(B\times B) R ∩ ( B × B )
若 ( x , y ) ∈ R ∩ ( B × B ) (x,y)\in R\cap(B\times B) ( x , y ) ∈ R ∩ ( B × B ) ( y , z ) ∈ R ∩ ( B × B ) (y,z)\in R\cap(B\times B) ( y , z ) ∈ R ∩ ( B × B ) ( x , y ) ∈ R (x,y)\in R ( x , y ) ∈ R ( y , z ) ∈ R (y,z)\in R ( y , z ) ∈ R R R R ( x , z ) ∈ R (x,z)\in R ( x , z ) ∈ R ( x , y ) ∈ B × B (x,y)\in B\times B ( x , y ) ∈ B × B ( y , z ) ∈ B × B (y,z)\in B\times B ( y , z ) ∈ B × B B × B B\times B B × B B B B E B E_B E B ( x , z ) ∈ B × B (x,z)\in B\times B ( x , z ) ∈ B × B ( x , z ) ∈ R ∩ ( B × B ) (x,z)\in R\cap(B\times B) ( x , z ) ∈ R ∩ ( B × B ) R ∩ ( B × B ) R\cap(B\times B) R ∩ ( B × B )
全序关系:
设 ( A , ≤ ) (A,\leq) ( A , ≤ ) x , y ∈ A x,y\in A x , y ∈ A x ≤ y x\leq y x ≤ y y ≤ x y\leq x y ≤ x x x x y y y 可比 ;否则称 x x x y y y 不可比 。一个偏序集的子集,其中任意两个元素都可比,则称该子集为一条链 。
如果 ( A , ≤ ) (A,\leq) ( A , ≤ ) ≤ \leq ≤ 全序关系(totally ordering relation) ,称 ( A , ≤ ) (A,\leq) ( A , ≤ ) 全序集(totally ordered set) 。
一个偏序集的子集不一定为偏序集,但也满足
( A , R ) ⇒ ( B , R ∩ ( B × B ) ) , B ⊆ A (A,R)\Rightarrow(B,R\cap(B\times B)),\quad B\subseteq A
( A , R ) ⇒ ( B , R ∩ ( B × B )) , B ⊆ A
拟序关系:
设 R R R A A A R R R 反自反性、传递性 ,则称 R R R 拟序关系(quasi-ordering relation) ,通常写为 < < <
拟序关系隐含了反对称性 。
证明:
若 R = ∅ R=\emptyset R = ∅ R R R
若 R ≠ ∅ R\neq\emptyset R = ∅ ( x , y ) ∈ R (x,y)\in R ( x , y ) ∈ R x R y xRy x R y R R R x ≠ y x\neq y x = y R R R x , y x,y x , y x R y , y R x xRy,yRx x R y , y R x x R x xRx x R x x R y xRy x R y y R x yRx y R x R R R
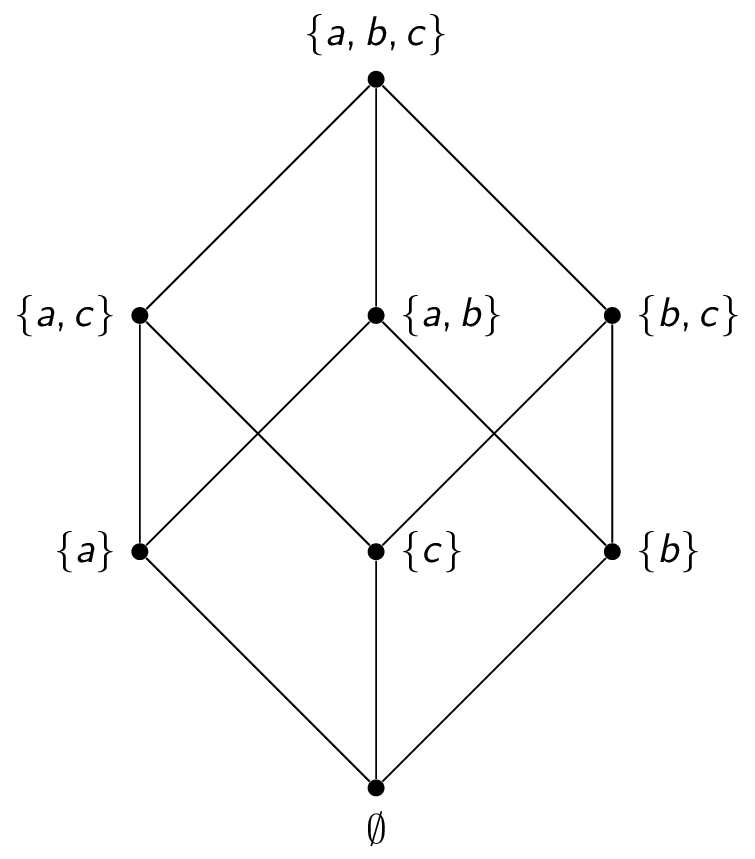
哈斯图(Hasse diagram):
哈斯图以平面上的点代表偏序集中的元素:
若两元素 x ≤ y x\leq y x ≤ y x ≠ y x\neq y x = y
将 x x x y y y
若没有不同于 x , y x,y x , y z z z x ≤ z ≤ y x\leq z\leq y x ≤ z ≤ y y y y x x x x , y x,y x , y
设 ( A , ≤ ) (A,\leq) ( A , ≤ )
如果 A A A a a a x ∈ A x\in A x ∈ A x ≤ a ( a ≤ x ) x\leq a\ (a\leq x) x ≤ a ( a ≤ x ) a a a A A A 最大元(最小元) 。
如果 A A A a a a x ∈ A x\in A x ∈ A a ≤ x ( x ≤ a ) a\leq x\ (x\leq a) a ≤ x ( x ≤ a ) a a a A A A 极大元(极小元) 。
对于 A A A M M M a ∈ A a\in A a ∈ A m ∈ M m\in M m ∈ M m ≤ a ( a ≤ m ) m\leq a\ (a\leq m) m ≤ a ( a ≤ m ) a a a M M M 上界(下界) 。
对于 A A A M M M M M M a a a M M M x x x a ≤ x a\leq x a ≤ x a a a M M M 上确界 。
对于 A A A M M M M M M a a a M M M x x x x ≤ a x\leq a x ≤ a a a a M M M 下确界 。
定理: 设 ( A , ≤ ) (A,\leq) ( A , ≤ ) B ⊆ A B\subseteq A B ⊆ A
若 b b b B B B b b b B B B
若 b b b B B B b ∈ B b\in B b ∈ B b b b B B B
若 B B B
映射
设 A , B A,B A , B A A A a a a B B B b b b A A A B B B 映射(mapping) ,记作 σ \sigma σ
σ ( a ) = b \sigma(a)=b
σ ( a ) = b
b b b a a a 像(image) ,a a a b b b 原像(pre-image) ,集合 A A A σ \sigma σ 定义域(domain) ,σ \sigma σ
σ ( A ) = { b ∣ σ ( a ) = b , ∀ a ∈ A } \sigma(A)=\{b|\sigma(a)=b,\forall a\in A\}
σ ( A ) = { b ∣ σ ( a ) = b , ∀ a ∈ A }
显然,σ ( A ) \sigma(A) σ ( A ) B B B
映射的关系定义法: 设 A , B A,B A , B σ \sigma σ A A A B B B a ∈ A a\in A a ∈ A B B B b b b ( a , b ) ∈ σ (a,b)\in\sigma ( a , b ) ∈ σ σ \sigma σ A A A B B B
设集合 A A A m m m B B B n n n A A A B B B n m n^m n m
映射的分类
1. 满射: σ \sigma σ A A A B B B ∣ A ∣ ≥ ∣ B ∣ |A|\geq|B| ∣ A ∣ ≥ ∣ B ∣ B B B A A A σ \sigma σ A A A B B B 满射(surjective onto) 。
2. 单射: σ \sigma σ A A A B B B ∣ A ∣ ≤ ∣ B ∣ |A|\leq|B| ∣ A ∣ ≤ ∣ B ∣ a , b ∈ A a,b\in A a , b ∈ A a ≠ b a\neq b a = b σ ( a ) ≠ σ ( b ) \sigma(a)\neq\sigma(b) σ ( a ) = σ ( b ) σ \sigma σ A A A B B B 单射(injection) 。
3. 双射(一一映射): σ \sigma σ A A A B B B ∣ A ∣ = ∣ B ∣ |A|=|B| ∣ A ∣ = ∣ B ∣ σ \sigma σ A A A B B B A A A B B B σ \sigma σ A A A B B B 双射(bijection) ,或一一映射(one-to-one correspondence) 。
逆映射
设 A , B A,B A , B σ \sigma σ A A A B B B σ \sigma σ σ − 1 \sigma^{-1} σ − 1 σ \sigma σ 逆映射(inverse mapping) 。
对任意 a ∈ A a\in A a ∈ A
σ − 1 ( σ ( a ) ) = a \sigma^{-1}(\sigma(a))=a
σ − 1 ( σ ( a )) = a
推论: 设 A , B A,B A , B σ \sigma σ A A A B B B σ − 1 \sigma^{-1} σ − 1 B B B A A A
交集的逆映射满足:
σ − 1 ( A ∩ B ) ⊆ σ − 1 ( A ) ∩ σ − 1 ( B ) \sigma^{-1}(A\cap B)\subseteq\sigma^{-1}(A)\cap\sigma^{-1}(B)
σ − 1 ( A ∩ B ) ⊆ σ − 1 ( A ) ∩ σ − 1 ( B )
映射的乘积
设 σ \sigma σ A A A B B B τ \tau τ B B B C C C τ ⋅ σ \tau\cdot\sigma τ ⋅ σ τ \tau τ σ \sigma σ a ∈ A a\in A a ∈ A
( τ ⋅ σ ) ( a ) = τ ( σ ( a ) ) (\tau\cdot\sigma)(a)=\tau(\sigma(a))
( τ ⋅ σ ) ( a ) = τ ( σ ( a ))
映射的乘积满足结合律,但是不满足交换律。
( σ ⋅ ( τ ⋅ ρ ) ) ( x ) = ( ( σ ⋅ τ ) ⋅ ρ ) ( x ) = σ ( τ ( ρ ( x ) ) ) (\sigma\cdot(\tau\cdot\rho))(x)=((\sigma\cdot\tau)\cdot\rho)(x)=\sigma(\tau(\rho(x)))
( σ ⋅ ( τ ⋅ ρ )) ( x ) = (( σ ⋅ τ ) ⋅ ρ ) ( x ) = σ ( τ ( ρ ( x )))
将集合 M M M 恒等映射(identity mapping) I I I τ ⋅ σ = σ ⋅ τ = I \tau\cdot\sigma=\sigma\cdot\tau=I τ ⋅ σ = σ ⋅ τ = I τ , σ \tau,\sigma τ , σ τ = σ − 1 \tau=\sigma^{-1} τ = σ − 1
集合的可数性
基数
基数(cardinal number) ,是在集合论中被用于刻画任意集合大小的一个概念,也称为集合的势。设 A , B A,B A , B A A A B B B A A A B B B 基数相同(对等,等势或等浓) ,记作 ∣ A ∣ = ∣ B ∣ |A|=|B| ∣ A ∣ = ∣ B ∣
集合的等势关系是一个等价关系 。集合按照等势关系分成等价类,每个等价类的共同的数量特征,称为该等价类中集合的基数。
集合基数的不对等关系 ≤ \leq ≤ 偏序关系 。若 A A A B B B ∣ A ∣ ≤ ∣ B ∣ |A|\leq |B| ∣ A ∣ ≤ ∣ B ∣ A A A B B B A A A B B B ∣ A ∣ < ∣ B ∣ |A|<|B| ∣ A ∣ < ∣ B ∣
基数的三歧性定理(trifideity theorem): A , B A,B A , B ∣ A ∣ < ∣ B ∣ |A|<|B| ∣ A ∣ < ∣ B ∣ ∣ A ∣ = ∣ B ∣ |A|=|B| ∣ A ∣ = ∣ B ∣ ∣ B ∣ < ∣ A ∣ |B|<|A| ∣ B ∣ < ∣ A ∣
康托尔-伯恩斯坦定理(Cantor-Bernstein theorem): A A A A ′ A' A ′ B B B B ′ B' B ′ ∣ A ∣ = ∣ B ′ ∣ |A|=|B'| ∣ A ∣ = ∣ B ′ ∣ ∣ B ∣ = ∣ A ′ ∣ |B|=|A'| ∣ B ∣ = ∣ A ′ ∣ ∣ A ∣ = ∣ B ∣ |A|=|B| ∣ A ∣ = ∣ B ∣ ∣ A ∣ ≤ ∣ B ∣ |A|\leq|B| ∣ A ∣ ≤ ∣ B ∣ ∣ B ∣ ≤ ∣ A ∣ |B|\leq |A| ∣ B ∣ ≤ ∣ A ∣ ∣ A ∣ = ∣ B ∣ |A|=|B| ∣ A ∣ = ∣ B ∣
可数集合
一个集合,如果它的元素为有限个,或者它的元素与自然数集合之间存在双射,则称此集合为可数集合 。否则称该集合为不可数集合 。元素不是有限的可数集合称为可数无穷集合 。
藉由定义,我们可以得到集合 A A A A A A A = { a 1 , a 2 , ⋯ , a n , ⋯ } A=\{a_1,a_2,\cdots,a_n,\cdots\} A = { a 1 , a 2 , ⋯ , a n , ⋯ }
定理:
设 A 1 , A 2 , ⋯ , A n , ⋯ A_1,A_2,\cdots,A_n,\cdots A 1 , A 2 , ⋯ , A n , ⋯ ⋃ i = 1 ∞ A i \displaystyle\bigcup_{i=1}^\infty A_i i = 1 ⋃ ∞ A i
设 A , B A,B A , B A × B A\times B A × B A 1 , A 2 , ⋯ , A n A_1,A_2,\cdots,A_n A 1 , A 2 , ⋯ , A n A 1 × A 2 × ⋯ × A n A_1\times A_2\times\cdots\times A_n A 1 × A 2 × ⋯ × A n
可数集合的子集仍为可数集合。
有理数集合 Q \mathbb Q Q
实数集 R \mathbb R R ( a , + ∞ ) (a,+\infty) ( a , + ∞ ) [ a , b ] [a,b] [ a , b ] [ a , b ) [a,b) [ a , b ) ( a , b ] ( a ≠ b ) (a,b]\ (a\neq b) ( a , b ] ( a = b ) ( 0 , 1 ) (0,1) ( 0 , 1 ) [ 0 , 1 ] [0,1] [ 0 , 1 ] c c c
设 A 1 , A 2 , ⋯ , A n , ⋯ A_1,A_2,\cdots,A_n,\cdots A 1 , A 2 , ⋯ , A n , ⋯ c c c ⋃ i = 1 ∞ A i \displaystyle\bigcup_{i=1}^\infty A_i i = 1 ⋃ ∞ A i c c c c c c c c c
证明 ( 0 , 1 ) (0,1) ( 0 , 1 )
假设我们可以将 ( 0 , 1 ) (0,1) ( 0 , 1 )
{ P 1 = 0. a 11 a 12 a 13 ⋯ P 2 = 0. a 21 a 22 a 23 ⋯ P 3 = 0. a 31 a 32 a 33 ⋯ ⋮ P k = 0. a k 1 a k 2 a k 3 ⋯ a k k ⋯ ⋮ \begin{cases}
P_1=0.a_{11}a_{12}a_{13}\cdots\\
P_2=0.a_{21}a_{22}a_{23}\cdots\\
P_3=0.a_{31}a_{32}a_{33}\cdots\\
\quad\vdots\\
P_k=0.a_{k1}a_{k2}a_{k3}\cdots a_{kk}\cdots\\
\quad\vdots
\end{cases} ⎩ ⎨ ⎧ P 1 = 0. a 11 a 12 a 13 ⋯ P 2 = 0. a 21 a 22 a 23 ⋯ P 3 = 0. a 31 a 32 a 33 ⋯ ⋮ P k = 0. a k 1 a k 2 a k 3 ⋯ a kk ⋯ ⋮
考虑下面的数:
0. r 1 r 2 ⋯ r k ⋯ ( k = 1 , 2 , ⋯ ) 0.r_1r_2\cdots r_k\cdots\quad(k=1,2,\cdots)
0. r 1 r 2 ⋯ r k ⋯ ( k = 1 , 2 , ⋯ )
其中
r k = { 1 a k k ≠ 1 2 a k k = 1 r_k=\begin{cases}
1&a_{kk}\neq 1\\
2&a_{kk}=1\\
\end{cases} r k = { 1 2 a kk = 1 a kk = 1
显然,这个数是 ( 0 , 1 ) (0,1) ( 0 , 1 ) 0. a k 1 a k 2 a k 3 ⋯ a k k ⋯ 0.a_{k1}a_{k2}a_{k3}\cdots a_{kk}\cdots 0. a k 1 a k 2 a k 3 ⋯ a kk ⋯ r k ≠ a k k r_k\neq a_{kk} r k = a kk
0. a k 1 a k 2 a k 3 ⋯ a k k ⋯ ≠ 0. r 1 r 2 ⋯ r k ⋯ 0.a_{k1}a_{k2}a_{k3}\cdots a_{kk}\cdots\neq 0.r_1r_2\cdots r_k\cdots
0. a k 1 a k 2 a k 3 ⋯ a kk ⋯ = 0. r 1 r 2 ⋯ r k ⋯
与我们的假设产生矛盾,所以 ( 0 , 1 ) (0,1) ( 0 , 1 )
判断可数集合的方法:
按照可数集合的定义,若 A A A A A A A A A A A A
若 A A A A A A
若 A A A A A A
若 A A A n ( n > 1 ) n\ (n>1) n ( n > 1 ) A A A
若 A A A A A A
若 A A A n ( n > 1 ) n\ (n>1) n ( n > 1 ) A A A
康托尔定理(Cantor’s theorem): A A A A A A
证明:
假设 σ \sigma σ A A A ρ ( A ) \rho(A) ρ ( A )
B = { x ∣ x ∈ A ∧ x ∉ σ ( x ) } B=\{x\mid x\in A\wedge x\notin\sigma(x)\}
B = { x ∣ x ∈ A ∧ x ∈ / σ ( x )}
显然,B ⊆ A B\subseteq A B ⊆ A b ∈ A b\in A b ∈ A σ ( b ) = B \sigma(b)=B σ ( b ) = B
若 b ∈ B b\in B b ∈ B b ∉ σ ( b ) = B b\notin\sigma(b)=B b ∈ / σ ( b ) = B b ∉ B b\notin B b ∈ / B σ ( b ) = B \sigma(b)=B σ ( b ) = B b ∉ σ ( b ) b\notin\sigma(b) b ∈ / σ ( b ) b ∈ B b\in B b ∈ B
综上所述,不存在 A A A ρ ( A ) \rho(A) ρ ( A )
∣ A ∣ < ∣ ρ ( A ) ∣ |A|<|\rho(A)|
∣ A ∣ < ∣ ρ ( A ) ∣
连续统问题
我们可以构造基数任意大的集合,如 ∣ R ∣ < ∣ ρ ( R ) ∣ < ⋯ |\mathbb R|<|\rho(\mathbb R)|<\cdots ∣ R ∣ < ∣ ρ ( R ) ∣ < ⋯
按照基数的大小可以排列为:
0 , 1 , 2 , ⋯ , n , ⋯ , ℵ 0 , ℵ 1 , ℵ 2 , ⋯ 0,1,2,\cdots,n,\cdots,\aleph_0,\aleph_1,\aleph_2,\cdots
0 , 1 , 2 , ⋯ , n , ⋯ , ℵ 0 , ℵ 1 , ℵ 2 , ⋯
所谓连续统问题(continuum hypothesis) ,即已知 ℵ 0 < c \aleph_0<c ℵ 0 < c ℵ 1 < c \aleph_1<c ℵ 1 < c
连续统假设 为 ℵ 1 = c \aleph_1=c ℵ 1 = c
连续统假设无法在目前已有的集合论公理下被证明或证伪。